一道高考抛物线试题的探究与溯源
刘 刚 赵 毅
(北京市第十二中学高中部,100071)
○数学探究○
一道高考抛物线试题的探究与溯源
刘 刚 赵 毅
(北京市第十二中学高中部,100071)
一、题目
在直角坐标系xOy中,直线l:y=t(t≠0)交y轴于点M,交抛物线C:y2=2px(p>0)于点P,M关于点P的对称点为N,连结ON并延长交C于点H.
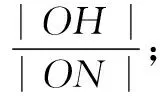
(2)除点H以外,直线MH与C是否有其它公共点?说明理由.
这是2016年的全国高考题.试题考查了抛物线的标准方程、中点坐标公式、直线与抛物线的位置关系及定值问题;考查了方程、转化与化归等数学思想以及坐标法的应用,检验了运算求解、分析问题与解决问题的能力.试题内涵丰富,是一道好题.
二、解法探究
分析第(1)问可根据已知条件写出点M的坐标,然后借助抛物线方程表示出点P的坐标.根据N为M关于点P的对称点求出点N的坐标,然后联立直线ON与抛物线的方程求出点N的坐标,分析点O、H、N坐标之间的关系求得答案.
第(2)问求出直线MH的方程,然后与抛物线的方程联立,由方程组解的个数进行判断.
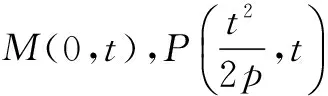
px2-2t2x=0,解得

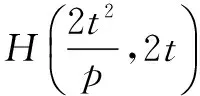
(2)直线MH与C除H以外没有其它公共点.理由如下:
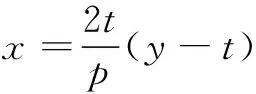
代入y2=2px,得
y2-4ty+4t2=0,
解得y1=y2=2t,
即直线MH与C只有一个公共点,所以除H以外直线MH与C没有其它公共点.由此可知,直线MH是抛物线C的一条切线.
三、试题溯源
在《圆锥曲线的几何性质》一书第1章抛物线中,有命题14:如图1,如果作抛物线的一对切线OQ,OQ′,并且作平行于轴的直线OV,交QQ′于V,那么QQ′被点V平分.

很明显,这道高考题就是在这个命题的基础上进行命制的,把这个命题重新梳理、拓展,可得以下结论.
结论如图2,过点P作抛物线C:x2=2py(p>0)的切线PA,PB,切点分别为A,B,过点P作x轴的垂线交AB于点M,交抛物线C于点N,过点N作抛物线C的切线l,则
(1)点M为线段AB的中点;
(2)点N为线段PM的中点;
(3)AB∥l.


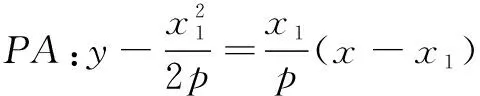
因为点P在切线PA上,所以
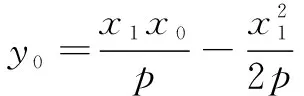
①
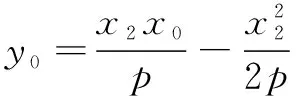
②
① -②,得

所以M为线段AB的中点.




四、高考试题链接
以上述命题14及所得结论为背景的高考试题屡见不鲜,下面再举几例,请读者自行完成.
例2(2008年山东高考题) 如图3,设抛物线方程为C:x2=2py(p>0),M为直线y=-2p上任意一点,过点M引抛物线的切线,切点分别为A,B.
(1)求证:A,M,B三点的横坐标成等差数列;
(2),(3)略.

例3(2008年陕西高考题) 如图4,已知抛物线C:y=2x2,直线y=kx+2交C于A,B两点,M是线段AB的中点,过点M作x轴的垂线交C于点N.
(1)证明:抛物线C在点N处的切线与AB平行;(2)略.

例4(2007年江苏高考题)如图5,在平面直角坐标系xOy中,过y轴正方向上一点C(0,c)任作一直线,与抛物线y=x2相交于A,B两点.一条垂直于x轴的直线,分别与线段AB和直线l:y=-c交于点P,Q.
(2)若P为线段AB的中点,求证:QA为此抛物线的切线;
(3)试问(2)的逆命题是否成立?说明理由.

从2016年这道高考题的探究及背景溯源来看,在平时的教学中要引导学生加强知识储备,建立知识间的联系,明确处理解析几何试题的思想与方法.提倡一题多解、一题多变、多题一解,从不同的角度理解与认识,尤其作为高考题.在圆锥曲线中,有很多有趣的结论与性质,教师可以带领感兴趣的学生进一步研究,这样,在解决圆锥曲线试题时就会得心应手,游刃有余.
所以DE2=a2+b2

