一个定值问题的推广
张仁华
(江苏省启东市汇龙中学,226200)
一个定值问题的推广
张仁华
(江苏省启东市汇龙中学,226200)

(1)求圆O的方程.
(2)若直线l与圆O切于第一象限,且与坐标轴交于点D、E,当DE长最小时,求直线l的方程.
(3)设M、P是圆O上任意两点,点M关于x轴的对称点为N.若直线MP、NP分别交x轴于点(m,0)和(n,0),问mn是否为定值?若是,请求出该定值;若不是,请说明理由.

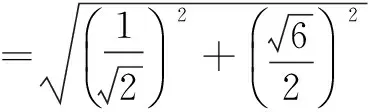
故圆O的方程为x2+y2=2.
(2)设直线l的方程为
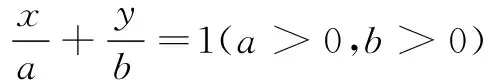
即 bx+ay-ab=0.
由直线l与圆O相切,得
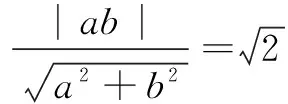


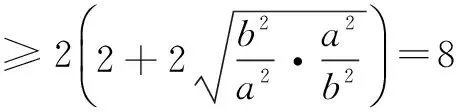
当且仅当a=b=2时等号成立,此时直线l的方程为x+y-2=0.
(3)设M(x1,y1),P(x2,y2),则N(x1,-y1),
x21+y21=2,x22+y22=2.
故mn=2为定值.
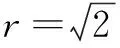
推广1能否推广到一般的圆呢?
推广到圆的一般形式:设M、P是圆O:x2+y2=r2上任意两点,点M关于x轴的对称点为N.若直线MP、NP分别交x轴于点(m,0)和(n,0),问mn是否为定值?若是,请求出该定值;若不是,请说明理由.
解设M(x1,y1),P(x2,y2),则N(x1,-y1),x21+y21=r2,x22+y22=r2.
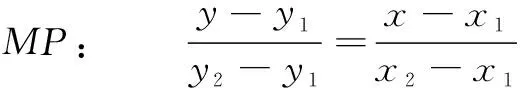

故mn=r2为定值.
评析也可先用特殊法取P(r,0),M(0,r),N(0,-r),得m=n=r,所以mn=r2,然后证明.
圆与椭圆有着密切的关系,可以通过伸缩变换相互转化.因而可以将把圆的问题类比推理到椭圆的情形.
推广2问题能否推广到椭圆呢?
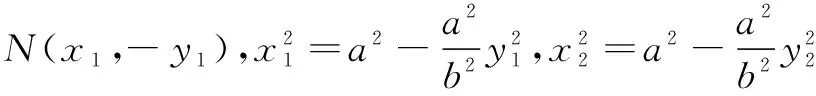
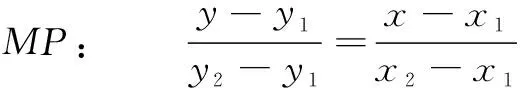

故mn=a2(定值).
椭圆是圆锥曲线的一种类型,它在定义、方程结构、几何特征等方面与双曲线有着许多共同的特性,所以运用类比的思想方法,可以大胆猜想双曲线的类似性质.
推广3问题能否推广到双曲线呢?
此推广可仿照推广2,解得mn=a2为定值.
推广4问题能否推广到抛物线呢?
类比到抛物线:设M、P是抛物线C:y2=2px(p>0)上任意两点,点M关于x轴的对称点为N,若直线MP、NP分别交x轴于点(m,0)和(n,0),问mn是否为定值?若是,请求出该定值;若不是,请说明理由.
解设M(x1,y1),P(x2,y2),则N(x1,-y1),由推广2,得

所以mn不是定值.


故m+n=0是定值,所以可得下列变式.
变式1设M、P是抛物线C:y2=2px(p>0)上任意两点,点M关于x轴的对称点为N.若直线MP、NP分别交x轴于点(m,0)和(n,0),问m+n是否为定值?若是,请求出该定值;若不是,请说明理由.
推广5问题可否推广到有心二次曲线?
设M、P是有心二次曲线C:ax2+by2=1(ab≠0)上任意两点,点M关于x轴的对称点为N.若直线MP、NP分别交x轴于点(m,0)和(n,0),问mn是否为定值?若是,请求出该定值;若不是,请说明理由.
类似地,由类比推理和二次曲线的对称性可得如下变式.

变式3设M、P是抛物线C:x2=2py(p>0)上任意两点,点M关于y轴的对称点为N,若直线MP、NP分别交y轴于点(0,m)和(0,n),则m+n是定值0.
——从广州一模的一道选择题谈起

