基于区间直觉模糊集的空战训练命中评估群决策

侯西倩, 寇英信, 李战武, 徐 安, 葛亚维, 陈 通

(1. 空军工程大学航空航天工程学院, 陕西 西安 710038; 2. 中国人民解放军93735部队, 天津 301700)



基于区间直觉模糊集的空战训练命中评估群决策

侯西倩1,2, 寇英信1, 李战武1, 徐 安1, 葛亚维1, 陈 通1

(1. 空军工程大学航空航天工程学院, 陕西 西安 710038; 2. 中国人民解放军93735部队, 天津 301700)

为解决空战训练命中评估中存在的评估语言不一致、专家权重未知、多专家集结等群决策问题,提出了仿真模拟、区间直觉模糊集、群决策相结合的方法。利用仿真模拟构建四元命中评估指标集,集合专家经验,建立群决策模型,利用区间直觉模糊集和逼近理想解排序法(technique for order preference by similarity to ideal solution,TOPSIS)方法实现专家经验汇总与集结,利用模糊熵原理衡量专家评估结论的模糊度,获取专家权重,最终实现空战训练命中评估。在Matlab M文件中实现了评估模块的封装,并将处理后的数据输出到Excel表格中。结合实际空战训练数据进行验证,此方法可有效解决空战训练命中评估的群决策问题。

空战训练命中评估; 群决策; 区间直觉模糊集; 专家权重

0 引 言

空战训练命中评估时,一般由多个评估专家组成评估专家组进行,是一种评估群决策问题。评估群决策是指由一定组织形式的评估专家群,对现有的、已存在或发生的共同背景下的评估对象,按照一定的程序、遵循共同的评估准则,采用相同的评估体系,多名专家对评估对象做出价值判断的过程[1]。本文所指的空战训练命中评估,即对单射多枚导弹进行优劣评估。

文献[2]研究了群决策结果的影响因素,指出基于Internet的群决策支持系统能有效提高决策效率和满意度;文献[3]针对群决策中的信息集结问题,提出了基于语言变量的群决策算子和算法;文献[4]以群决策方法确定了武器装备体系排序评价的评估思路,该方法对不同武器装备体系排序具有高效性;文献[5]将模糊评价法、专家评价、理想化标尺评价与多目标决策理论相结合,对武器装备体系效能进行了有效评估;文献[6]在评价桥梁状态的问题上,探讨了集值统计理论与加权极值统计理论相互关系并应用,该方法为命中评估群决策问题提供了一定的参考。

随着武器装备的不断革新、新型战术战法的层出不穷以及战术协同的广泛应用,空战训练中的命中越来越难以测量与评价,命中评估需要借助更为精细的手段才能完成。为减少评估群决策中的非理性成分,本文将仿真模拟和区间直觉模糊集运用到传统评估群决策问题中,完成对评估群决策方法的优化,主要完成两个任务：一是群决策与仿真模拟结果相结合,进而实现定性分析与定量评估相结合,降低评估过程的随意性;二是利用智能算法集结专家群体的评估意见,提高评估的规范性。

1 基于仿真模拟法构建命中评估指标集

空战训练系统中,利用仿真模拟效能评估方法对武器发射命中进行仿真建模,不妨以某型中距空空导弹为例,得到以脱靶量、命中时间、命中精度、命中精度的无偏最小方差估计构建的评估指标集作为属性集。

1.1 脱靶量评估指标的建立

脱靶量是衡量导弹制导性能的重要参数,也是导弹最重要的战技指标之一。但由于弹道仿真模拟为离散仿真,通常在一次仿真步长Δt内,导弹的飞行距离大于导弹的杀伤半径,会导致仿真输出的脱靶量为负值或精度不够,而非导弹与目标之间的最小距离。本文采用牛顿插值法解决既定仿真步长Δt时间内估算脱靶量的问题。

不妨取t-2·Δt、t-Δt和t时刻的导弹与目标的相对距离Rt-2、Rt-1和Rt为插值节点,运用牛顿向后插值公式,得到时间和相对距离的二次插值曲线为

R=Rt-2+τ(Rt-2-Rt-1)+

(1)

1.2 命中时间评估指标的建立

导弹命中目标所需的飞行时间为命中时间,它直接关系控制系统及弹体参数的选择,是导弹武器系统设计的必要数据。

基于直观推断的命中时间求算方法——加速度的距离除以逼近速度(简称AROCV),为变速导弹提供了合理的飞行时间估计[8]。

1.3 命中概率评估指标的建立

命中概率是指应用蒙特卡罗法进行数学模拟打靶,对某一条弹道脱靶量进行统计,计算出导弹脱靶量期望和方差,从而得出导弹的命中概率[9]。当没有脱靶量，没有系统误差时,即m=0,此时,命中以R为半径的圆CR内的概率为

(2)

式中,σd为脱靶量的方差;r为弹着点极坐标表示中的极径。

1.4 命中精度评估指标的建立

命中精度是表征导弹性能的一个综合指标,可以用命中概率的置信区间值来衡量。对于n次射击中的弹着点(yi,zi)记:

(3)

则Ri服从χ(2)分布。记

T(R)为σ2的充分统计量。由Lehmann-Scheffe定理可知:

T*=E[S(R1)|T=t]

(4)

2 群区间直觉模糊集法的应用

2.1 群区间直觉模糊集的相关定义

文献[10]给出了区间模糊集的概念:

定义 1 设X是一个非空集合,则称

A={[x,μA(x),vA(x)]|x∈X}=

{〈x,[μAL(x),μAU(x)],[vAL(x),vAU(x)]〉|x∈X}

为区间直觉模糊集,其中μA(x)⊂[0,1]和vA(x)⊂[0,1],x∈X。

定义 2 设A∈IVIFS(X),那么区间直觉模糊数A的模糊熵被定义为

式中,∧,∨分别表示取最小值和最大值。

定义 3 论域X中的两个区间直觉模糊集A,B之间的模糊交叉熵为

式中,F1(A),F2(A)被称为模糊交叉熵算子。

F1(A)=μAL(x)+μAU(x)+2-vAL(x)-vAU(x)

F2(A)=2-μAL(x)-μAU(x)+vAL(x)+uAU(x)

定义 4 论域X中的两个区间直觉模糊集A,B之间的模糊交叉熵距离为

D(A,B)=I(A,B)+I(B,A)

由于专家评估语言的多样性和评估角度的不确定性,使得评估语言不统一,这就需要强大的模糊表述算法对不同专家的评估语言进行汇总。另外, 空战训练命中评估非实弹发射,仿真使命中评估具有一定的复杂性和不确定性,导致模糊集中的隶属度和非隶属度有时很难直接用精确的实数值来表达。因此本文选用区间直觉模糊集对评估语言进行描述[11]。

2.2 基于群区间直觉模糊集的命中评估建模

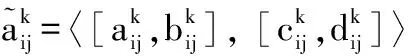
对于上述评估问题,本文将逼近理想解排序法(technique for order preference by similarity to ideal solution,TOPSIS)方法拓展到解决专家权重未知且专家评估信息为区间直觉模糊集的多属性群决策问题中,具体步骤如下。

步骤 1 正、负理想解求算为

(5)

式中,i=1,2,…,m;j=1,2,…,n;k=1,2,…,k。

步骤 2 分别计算出各专家评估方案与理想解和负理想解的距离。本文利用模糊交叉熵来衡量直觉模糊集之间的差距：

(6)

步骤 3 计算专家权重。专家的权重取决于专家评估信息的可靠性和确定性程度,专家权重能够反映各专家对评估的了解程度和分析粒度,因此本文选用模糊熵来衡量专家权重。利用信息熵确定专家权重的计算公式为

(7)

式中

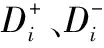
(8)

(9)

步骤 5 计算贴近度,选择最优方案

(10)

显然,Ci越大,表明被选方案Ai离正理想解的距离越小,离负理想解的距离越大,因而该评估结论越好。

3 群效能命中评估模型的Matlab M文件表达

Matlab提供了丰富的内部函数,是一个强大的数据处理工具。通过在Matlab里面编写M函数,并封装成一个函数接口,可以更加高效地完成用户所设定的工作,满足实际需求[12]。同时利用与Microsoft Excel丰富的接口功能,可以实现将计算出来的数据输出到Excel表格中,进而实现Excel对数据的直观分析,为进一步评估判断提供了方便。

该空战训练命中评估模型分成6个模块:导弹发射初始状态数据库模块、输入数据模块、四元命中评估指标计算模块、数据处理模块、计算结果输出模块、评估综合结果检验模块。空战训练命中评估模型作为空战训练评估软件部分的一个模型,以动态链接库(dynamic link library, DLL)的形式提供标准接口,供空战训练时调用,并将评估结果以Excel的形式显示出来[13]。

4 实例评估

根据某次空战训练单发多枚导弹的数据进行建模仿真,选用以下典型4枚某型导弹,求算发射后的命中评估指标值如表1所示。

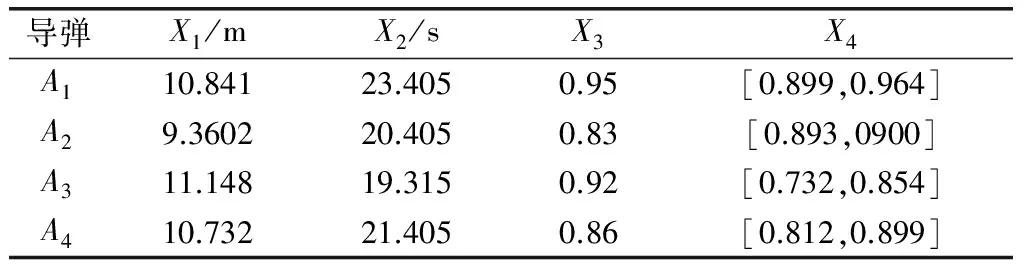
表1 4枚某型导弹的四元命中评估指标集

分析不同专家对上述四元命中评估指标的数值解进行满意度评估的实际情况,将各专家的语言表述和对评估指标值的打分构建区间直觉判断，如表2所示,并给出不同的评估指标权值。

根据式(5)取Excel表格中相应单元格的数据,在Matlab M函数中编程求算理想评估方案和负理想评估方案,并由定义3求算各专家的评估方案到理想评估结论的加权模糊交叉熵距离,将相应数据输出到Excel中显示，如表3所示。

按照式(7)求算专家权重向量为λ=(0.240,0.265,0.262,0.333),由式(8)和式(9)计算基于加权算数算子方法的各专家集结距离。最后根据式(10)求算各评估结论的贴近度,给出评估结论排序,可求得对于4个评估方案的排序为A2fA3fA4fA1。因此,第二枚导弹的命中评估结果为最优[14]。

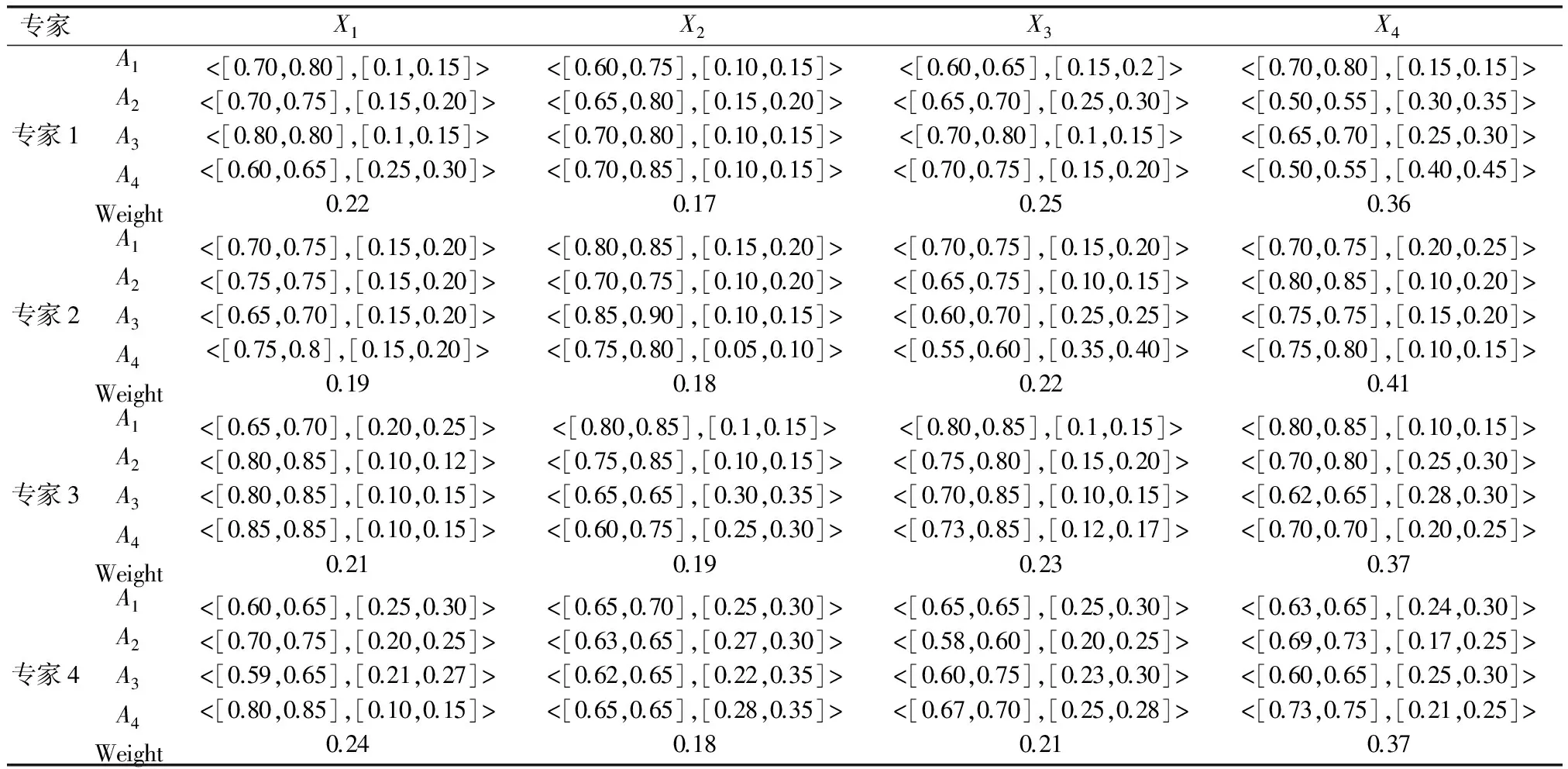
专家X1X2X3X4专家1A1A2A3A4Weight<[0．70，0．80]，[0．1，0．15]><[0．70，0．75]，[0．15，0．20]><[0．80，0．80]，[0．1，0．15]><[0．60，0．65]，[0．25，0．30]>0．22<[0．60，0．75]，[0．10，0．15]><[0．65，0．80]，[0．15，0．20]><[0．70，0．80]，[0．10，0．15]><[0．70，0．85]，[0．10，0．15]>0．17<[0．60，0．65]，[0．15，0．2]><[0．65，0．70]，[0．25，0．30]><[0．70，0．80]，[0．1，0．15]><[0．70，0．75]，[0．15，0．20]>0．25<[0．70，0．80]，[0．15，0．15]><[0．50，0．55]，[0．30，0．35]><[0．65，0．70]，[0．25，0．30]><[0．50，0．55]，[0．40，0．45]>0．36专家2A1A2A3A4Weight<[0．70，0．75]，[0．15，0．20]><[0．75，0．75]，[0．15，0．20]><[0．65，0．70]，[0．15，0．20]><[0．75，0．8]，[0．15，0．20]>0．19<[0．80，0．85]，[0．15，0．20]><[0．70，0．75]，[0．10，0．20]><[0．85，0．90]，[0．10，0．15]><[0．75，0．80]，[0．05，0．10]>0．18<[0．70，0．75]，[0．15，0．20]><[0．65，0．75]，[0．10，0．15]><[0．60，0．70]，[0．25，0．25]><[0．55，0．60]，[0．35，0．40]>0．22<[0．70，0．75]，[0．20，0．25]><[0．80，0．85]，[0．10，0．20]><[0．75，0．75]，[0．15，0．20]><[0．75，0．80]，[0．10，0．15]>0．41专家3A1A2A3A4Weight<[0．65，0．70]，[0．20，0．25]><[0．80，0．85]，[0．10，0．12]><[0．80，0．85]，[0．10，0．15]><[0．85，0．85]，[0．10，0．15]>0．21<[0．80，0．85]，[0．1，0．15]><[0．75，0．85]，[0．10，0．15]><[0．65，0．65]，[0．30，0．35]><[0．60，0．75]，[0．25，0．30]>0．19<[0．80，0．85]，[0．1，0．15]><[0．75，0．80]，[0．15，0．20]><[0．70，0．85]，[0．10，0．15]><[0．73，0．85]，[0．12，0．17]>0．23<[0．80，0．85]，[0．10，0．15]><[0．70，0．80]，[0．25，0．30]><[0．62，0．65]，[0．28，0．30]><[0．70，0．70]，[0．20，0．25]>0．37专家4A1A2A3A4Weight<[0．60，0．65]，[0．25，0．30]><[0．70，0．75]，[0．20，0．25]><[0．59，0．65]，[0．21，0．27]><[0．80，0．85]，[0．10，0．15]>0．24<[0．65，0．70]，[0．25，0．30]><[0．63，0．65]，[0．27，0．30]><[0．62，0．65]，[0．22，0．35]><[0．65，0．65]，[0．28，0．35]>0．18<[0．65，0．65]，[0．25，0．30]><[0．58，0．60]，[0．20，0．25]><[0．60，0．75]，[0．23，0．30]><[0．67，0．70]，[0．25，0．28]>0．21<[0．63，0．65]，[0．24，0．30]><[0．69，0．73]，[0．17，0．25]><[0．60，0．65]，[0．25，0．30]><[0．73，0．75]，[0．21，0．25]>0．37

表3 区间直觉模糊决策模糊交叉熵距离

5 结束语

本文提出了一种利用仿真模拟、区间直觉模糊集、群决策方法相结合的方法进行空战训练命中评估,结合区间直觉模糊集构建了群区间直觉模糊决策矩阵,改进了专家权重的确定方法,用专家提供的判断信息的模糊程度和不确定程度来决定专家的权重,很大程度上避免了主观性和权威垄断。理论和仿真结果表明,提出的方法可以评估不同导弹方案的命中优劣[15],为空战训练命中评估的实现和应用提供了客观、科学的依据。

[1] Bi C J, Dong D M.Operationalsimulationtrainingeffectivenessevaluation[M].Beijing: National Defense Industry Press, 2014. (毕长剑, 董冬梅. 作战模拟训练效能评估[M].北京: 国防工业出版社, 2014.)

[2] Beroggi G E G. Internet multi attribute group decision support in electronic commerce[J].GroupDecisionandNegotiation, 2003, 12(12): 481-499.

[3] Herrera F, Verdegay J L. Lingguistic assessments in group decision[C]∥Proc.ofthe1stEuropeanCongressonFuzzyandIntelligentTechnologicAachen, 1993: 941-948.

[4] Xu L S, Wang Z Q. An equipment evaluation method based on multi-attribute group decision-making theory[J].JournalofGunLaunch&Control, 2010(2): 1-4.(徐林生, 王执铨. 基于多属性群决策理论的武器装备体系评价方法[J].火炮发射与控制学报, 2010(2): 1-4.)

[5] Niu K, Pang Z B. A comprehensive method for effectiveness evaluation of weapon system[J].InformationCommandControlSystem&SimulationTechnology, 2005, 27(1): 50-53.(牛坤, 庞志兵. 基于多目标决策理论武器装备效能综合评估方法[J].情报指挥控制系统与仿真技术, 2005, 27(1): 50-53.)

[6] Sun J C, Shi J J. The application of right of set-valued statistics theory and barycenter decision theory in the bridge engineering[J].ShanghaiHighways, 2001(4): 20-22.(孙九春, 史家钧. 权集值统计理论和重心决策理论在桥梁评估中的应用[J].上海公路,2001(4): 20-22.)

[7] Shutty M A. Dynamic modeling and modal analysis of an air-to-air missile model[D]. Monterey: Naval Postgraduate School, 1992.

[8] Tahk M J, Ryoo C K, Cho H. Recursive time-to-go estimation for homing guidance missiles[J].AerospaceandElectronicSystems, 2002, 38(1): 13-23.

[9] Fu X Z, Hu X, Fang Y W, et al. A research of accuracy evaluation system of air-to-groud missile fall points[J].JournalofAirForceEngineeringUniversity, 2014, 15(5): 42-45.(傅修竹, 胡晓, 方洋旺, 等. 空地导弹落点精度评估系统[J].空军工程大学学报, 2014, 15(5): 42-45.)

[10] Boran F E, Genc S, Kurt M, et al. A multi-criteria intuitionistic fuzzy group decision making for supplier selection with TOPSIS method[J].ExpertSystemswithApplications, 2009, 36(8): 11363-11368.

[11] Xu Z S. A method based on distance measure for interval-valued intuitionistic fuzzy group decision making[J].InformationSciences, 2010, 180(1): 181-190.

[12] Huang Y Y, Lv C, Han S C. Notice of retraction combat description framework of the naval systems on multi-agent[C]∥Proc.oftheIEEEInternationalConferenceonAdvancesandManagementSciences, 2010：591-594.

[13] Tong Z X, Ye G Q, Lu Y L, et al. Method of evaluation of air-to-air combat effectiveness of simulations operated by pilots[J].JournalofSystemSimulation, 2007, 19(8): 1680-1695.(童中翔, 叶广强, 芦艳龙, 等.基于有驾驶员参与的多机空战模拟效能评估方法[J].系统仿真学报, 2007, 19(8): 1680-1695.)

[14] Kaplan J A, Chappell A R, McManus J W. The analysis of a generic air-to-air missile simulation model[R]. Hampton, Virginia: NASA Langley Technical Report Server, 2003.

[15] Panarisi M T. A comparative analysis of internal and external solutions to provide air combat maneuvering instrumentation (ACMI) functionality[D]. Alabama: Air University, 2000.

Group decision-making of air combat training accuracy assessment based on interval-valued intuitionist fuzzy set

HOU Xi-qian1,2, KOU Ying-xin1, LI Zhan-wu1, XU An1, GE Ya-wei1, CHEN Tong1

(1.AeronauticsandAstronauticsEngineeringCollege,AirForceEngineeringUniversity,Xi’an710038,China; 2.Unit93735ofthePLA,Tianjin301700,China)

With respect to the problems of the inconsistence of assessment language, unknown weight of the decision-makers, assembly of multiple experts in air combat training accuracy assessment, a new method which combines analogue simulation and interval-valued intuitionist fuzzy set with group decision-making is proposed. With analogue simulation, the index set of the accuracy assessment is built. Combining expertise, group decision-making model is built. With the interval-valued intuitionist fuzzy set and the technique for order preference by similarity to ideal solution (TOPSIS) method, the expertise is gathered and assembled. With the theory of fuzzy entropy, the weight of decision-makers is obtained through the measurement of fuzzy degree of the results. And finally, the air combat training accuracy assessment is realized. The packaging of the evaluated model is accomplished in the file of Matlab M, which is exported to the Excel tables. Applying the air combat training data to the verification, the method is effective to solve the problems of group decision-making in air combat training accuracy assessment.

air combat training accuracy assessment; group decision-making; interval-valued intuitionist fuzzy set; weight of the decision-makers

2015-06-29；

2016-02-27；网络优先出版日期：2016-06-19。

E 917

A

10.3969/j.issn.1001-506X.2016.12.16

侯西倩(1991-),女,硕士研究生,主要研究方向为空战训练评估、空战决策。

E-mail:783438669@qq.com

寇英信(1965-),男,教授,博士,主要研究方向为空战决策与评估。

E-mail:kgykyx@hotmail.com

李战武(1982-),男,副教授,硕士,主要研究方向为空战决策与评估。

E-mail:afeulzw@189.cn

徐 安(1984-),男,讲师,博士,主要研究方向为空战决策与评估。

E-mail:xuanot@163.com

葛亚维(1990-),男,博士研究生,主要研究方向为决策算法优化与融合。

E-mail:595930529@qq.com

陈 通(1992-),男,硕士研究生,主要研究方向为空战训练评估、空战决策。

E-mail:839447617@qq.com

网络优先出版地址：http://www.cnki.net/kcms/detail/11.2422.TN.20160619.1131.008.html