基于气浮台的交会对接相对姿态和位置控制

黄 成, 王 岩, 陈兴林

(哈尔滨工业大学控制科学与工程系, 黑龙江 哈尔滨 150001)



基于气浮台的交会对接相对姿态和位置控制

黄 成, 王 岩, 陈兴林

(哈尔滨工业大学控制科学与工程系, 黑龙江 哈尔滨 150001)

基于交会对接地面物理仿真系统对卫星交会对接中相对姿态和位置的控制问题进行研究,根据地面物理仿真系统的结构推导出描述系统姿态和位置运动的耦合六自由度动力学模型;基于此模型,在存在外部扰动的情况下,采用自适应快速非奇异终端滑模控制思想设计一种能够克服传统终端滑模控制奇异问题的鲁棒有限时间控制器。通过李雅普诺夫理论推导和仿真分析表明,该控制器在保证系统的有限时间稳定性和收敛性的同时能有效地抑制外部扰动。

气浮台; 六自由度耦合; 交会对接; 终端滑模; 自适应控制

0 引 言

近些年由于空间活动的不断增加,卫星交会对接技术已经成为一个重要的研究领域。许多空间任务的进行都应用了交会对接技术,例如捕捉空间对象、在轨装配、在轨维修。卫星交会对接的核心技术就是姿态同步和位置跟踪,这需要准确的相对姿态和位置控制[1]。如果没有实现姿态同步和位置跟踪,交会对接中追踪卫星的动作与目标卫星的动作将是不协调的,上面提到的空间任务将不能安全准确地得以实现。通常,对在轨卫星控制方法进行的测试和调整是风险极大的,六自由度气浮台可以在地面营造微重力的类空环境,应用其姿态平台能够进行高置信度的卫星姿态和轨道运动的地面物理仿真[2],因此在卫星在轨操作之前,在地面基于由两个六自由度气浮台组成的地面物理仿真系统对卫星交会对接中相对姿态和位置控制策略的研究和验证是很有必要的。然而现有的对于卫星姿态和位置控制的研究很少是基于气浮台进行的[3]。

由于交会对接中相对姿态运动和相对轨道运动都是非线性的且彼此是高度耦合的,所以控制器的设计要保证相对姿态和位置控制的高准确性。通常相对姿态和相对位置控制器的设计都是分开进行的[4]。在姿态同步控制器的设计中,状态反馈容错控制、虚拟结构控制、自适应控制、最优切换控制等被广泛应用[5-7];同时鲁棒控制、最优控制、滑模控制和H∞控制等技术被应用到位置跟踪控制器的设计中[8-10]。然而,在上述研究中相对姿态运动和相对轨道运动之间的动力学耦合作用被忽略了,这将严重影响交会对接中控制器的准确性。因此同时考虑姿态同步和位置跟踪的六自由度耦合控制将会是交会对接控制今后的研究重点。基于θ-D技术的次优控制被用来解决存在模型不确定性的卫星交会对接控制[11];文献[12]提出一种输出反馈自适应控制器，解决了存在测量噪声的航天器的交会对接控制问题;对于编队飞行和在轨服务这一类空间任务,输出反馈追踪控制和自适应学习同步控制等方法[13]被用来解决两个卫星之间相对姿态和位置控制问题。然而上述研究中的系统收敛速度较慢,只是保证了系统的渐进稳定,即当时间趋于无穷时状态误差才会收敛到平衡点。而随着空间技术的发展,对卫星控制策略收敛性能的要求越来越高,因此具有快速收敛性的有限时间控制框架下的方法被广泛地应用到卫星姿态控制中。文献[14]采用齐次性方法设计了一种航天器有限时间姿态跟踪控制器;在航天器执行机构存在故障的情况下,文献[15]基于终端滑模提出了有限时间姿态容错控制方法。然而在卫星姿态和位置耦合控制的设计上很少有研究应用了有限时间控制思想。另外,在控制器的设计过程中,需要考虑外部扰动对系统稳定性的影响。

为此,本文应用地面物理仿真系统模拟卫星交会对接过程,针对气浮台追踪器对气浮台目标器姿态同步和位置跟踪的综合控制问题,提出了一种六自由度耦合鲁棒有限时间控制器。该控制器考虑了交会对接中相对姿态运动和相对轨道运动的高度耦合性,有效地抑制了外部扰动;通过李雅普诺夫理论分析和仿真结果表明,该控制器保证了系统的有限时间收敛和稳定。

1 交会对接地面物理仿真系统

交会对接地面物理仿真系统[16]如图1所示,主要由两个可以实现6个自由度气浮无摩擦运动的六自由度气浮台组成。气浮台的姿态平台为卫星模拟器,两个卫星模拟器分别用来模拟交会对接中的追踪卫星和目标卫星,进而实现完整的卫星交会对接动力学和运动学仿真。

图1 交会对接地面物理仿真系统Fig.1 Physical ground simulation system for rendezvous and docking

六自由度气浮台如图2所示,由姿态平台(卫星模拟器)、水平运动平台和重力平衡伺服运动机构3个部分组成。球面气浮轴承支撑姿态平台且连接重力平衡伺服运动机构,伺服运动机构与水平运动平台连接,整个气浮台由3个平面气浮轴承支撑。通过执行机构的控制,姿态平台可以分别绕垂直于地面的坐标轴和两个水平方向的坐标轴无摩擦的转动,模拟卫星的姿态运动过程,同时可以沿着两个水平方向和垂直于地面方向气浮无摩擦的运动,模拟卫星的轨道运动过程。通常,姿态平台垂直方向上的运动是通过机械方法实现的,这将严重影响卫星轨道运动仿真实验的真实性,本文采用如图3所示的重力平衡伺服运动机构实现姿态平台的重力平衡和垂向漂浮运动,保证了姿态平台在6个自由度运动上对卫星的全物理仿真。

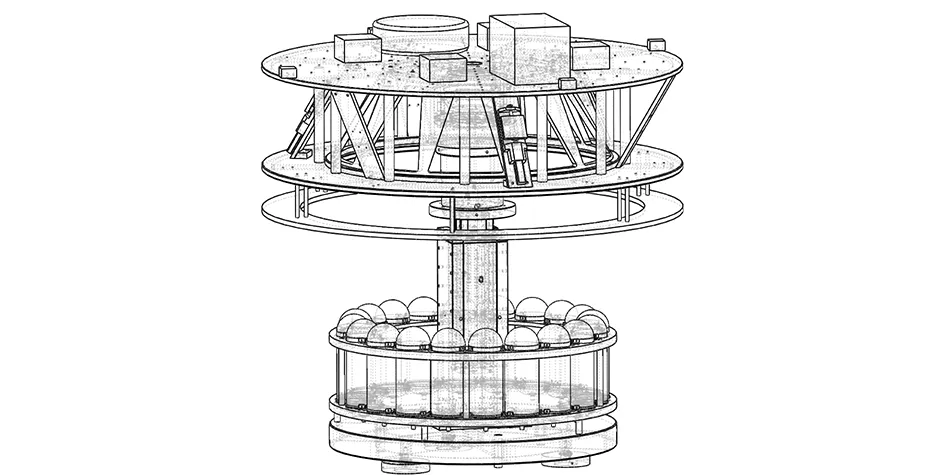
图2 六自由度气浮台整体结构Fig.2 Structure of the six DOF air bearing table

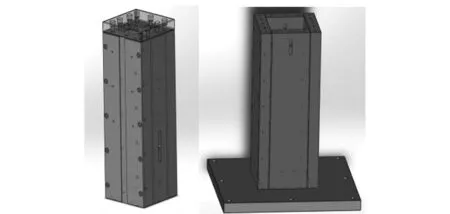
图3 垂向气浮轴承结构Fig.3 Vertical air bearing

2 六自由度耦合模型

2.1 气浮台追踪器和目标器的动力学模型

交会对接地面物理仿真系统的实施方案如图4所示,其中Fi{Oxiyizi}是以地面上一点为原点的平行于地心惯性坐标系的地面惯性坐标系,Fc{Cxcyczc}和Ft{Txtytzt}分别表示与气浮台追踪器和气浮台目标器固连的本体坐标系,原点分别是追踪器和目标器的旋转中心。Q点为沿着目标器对接端口方向且相对于目标器固定的点,是追踪器的要求位置。{rc,re}和{rt,rq,q}分别是坐标系Fc和Ft下的位置向量。本文的目的是控制追踪器完成旋转中心C对点Q的位置追踪,以及坐标系Fc对Ft的姿态追踪。

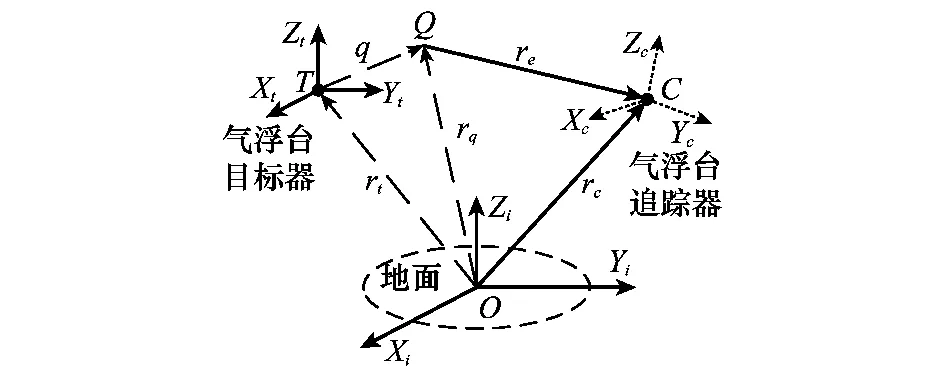
图4 交会对接地面物理仿真系统实施方案Fig.4 Scenario of the physical ground simulation system for rendezvous and docking

[a]×是对应于向量a=[ax,ay,az]T的叉乘矩阵：

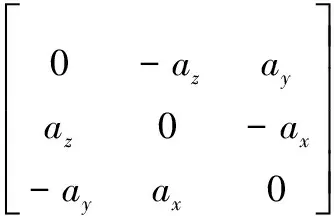
(1)

在Fc下,气浮台追踪器姿态和位置的运动学方程为

(2)

(3)

(4)

式中,rc,vc,ωc∈R3×1分别是追踪器的位置、速度和本体角速度;σ是修正罗德里格参数向量,用来描述追踪器相对于地面惯性坐标系Fi的姿态。

在Fc下,追踪器姿态和位置的动力学方程为

(5)

(6)

式中,m∈R,J∈R3×3分别是追踪器的质量和惯性矩阵;f,u∈R3×1分别是控制力和控制力矩;df,dτ∈R3×1分别是扰动力和扰动力矩。

同理,在Ft下,气浮台目标器姿态和位置的运动学和动力学方程为

(7)

(8)

(9)

(10)

(11)

式中,rt,vt,σt,ωt∈R3×1分别是目标器的位置、速度、姿态和本体角速度;mt∈R,Jt∈R3×3分别是目标器的质量和惯性矩阵。

2.2 相对运动动力学模型

气浮台追踪器对目标器的相对姿态为

(12)

从坐标系Ft到坐标系Fc的旋转矩阵为

(13)

根据图4可知,在Ft下,Q点的位置和速度为

rq=rt+q,vq=vt+[ωt]×q

(14)

式中,q∈R3×1是Ft下的常向量。追踪器对于目标器Q点的相对位置、相对速度和相对角速度在Fc下表示为

(15)

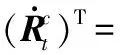
(16)

(17)

(18)

(19)

(20)

式中,G(σe)是可逆的。由式(11)、式(14)和式(15)可得

(21)

由式(10)和式(15)可得

(22)

将式(21)和式(22)代入式(19)和式(20),相对运动动力学模型可进一步表示为

(23)

(24)

其中

(ωc-ωe)-J[ωc]×ωe

根据追踪器对目标器相对运动的动力学和运动学模型可知,相对姿态运动和相对轨道运动之间的动力学和运动学耦合作用在c1、c2和c3的形式中得到了体现。

2.3 六自由度耦合动力学模型

引入状态变量x1=[σe;re]和x2=[ωe;ve],包含相对姿态运动和相对轨道运动的六自由度耦合动力学模型为

(25)

其中

3 控制器的设计

本文的控制目标是驱动气浮台追踪器沿着与气浮台目标器对接的方向完成对Q点位置的跟踪,同时确保追踪器姿态与目标器姿态的同步。为此,本节应用自适应控制和终端滑模控制的思想设计一种鲁棒有限时间控制器。

为了方便控制器的设计,首先给出如下引理和假设[17]。

引理 1 当α1,α2,…,αn都为正数时,对于0<ρ<2,不等式(26)成立。

(26)

(27)

假设 1d是有界的但界限未知,气浮台目标器的角速度、角加速度、速度和加速度都是有界的。

传统终端滑模面S=[S1,S2,S3]T，如式(28)所示,其中θ1和θ2是正数,q>p>0是整数且是奇数。

(28)

式(28)对时间求导可得

(29)

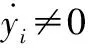
为解决上述两个问题,快速非奇异终端滑模面设计为

(30)

(31)

式中,i=1,2,3,4,5,6。

r1=(2-γ)ηγ-1,r2=(γ-1)ηγ-2

(32)

sig(x1,i)γ=|x1,i|γsign(x1,i)

(33)

式中,α>0,β>0,0<γ<1。

基于终端滑模面式(30),控制器设计为

(34)

(35)

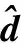
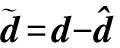
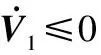
定理 1 由式(25)描述的交会对接地面物理仿真系统,在控制器式(34)和式(35)的作用下,可以实现如下目标。

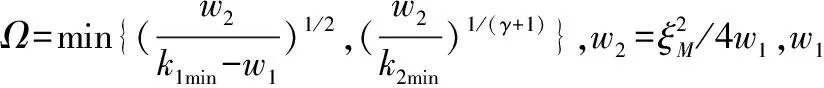
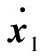
Δ=Ω+αΛ+βΛγ

STξ≤-k1minSTS-k2minSTsig(S)γ+

取η1=2(k1min-w1),η2=2(γ+1)/2k2min,则上式变为

(36)

将式(36)右侧中的w2分别与前两项组合可得

(37)

(38)

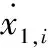
当|x1,i|≤η(i=1,2,3,4,5,6),由式(30)和式(31)可得

(39)

(40)

当|x1,i|>η(i=1,2,3,4,5,6),由式(30)和式(31)可得

(41)

将上式右侧中Ω分别与第一项和第二项组合可得

(42)

(43)

至此定理1得证。

证毕

总结 1 由控制器式(34)可知增益K1和K2是6维对角矩阵的形式,前3个对角线元素对应相对姿态控制,后3个对角线元素对应相对位置控制,因此这两部分的增益可单独设计来满足各自的带宽。

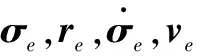
4 仿真校验

为了验证所设计控制方法的有效性,本节基于地面物理仿真系统进行卫星交会对接模拟,并进行数值仿真研究。

气浮台追踪器的初始运动状态及其与气浮台目标器的相对初始运动状态如表1所示,目标器的姿态和轨道信息为随时间改变的正弦余弦信号。

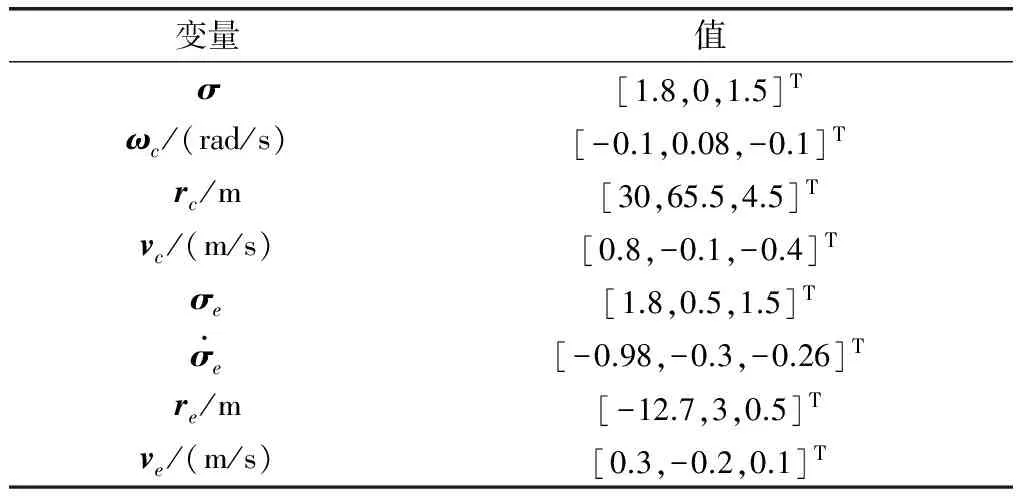
表1 初始值

追踪器和目标器的转动惯量分别为

,

控制器式(34)和式(35)的参数选择如下:

α=0.125,β=0.01,γ=0.5,η=0.000 01,E=I3

K1=diag([0.5,0.5,0.5,0.2,0.2,0.2])

K2=diag([2.5,2.5,2.5,0.8,0.8,0.8])

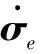
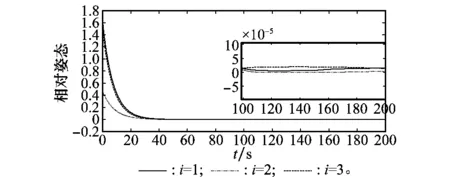
图5 相对姿态σe曲线Fig.5 Curves of relative attitude σe

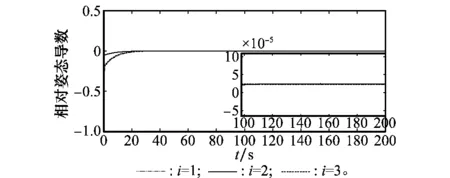
图6 相对姿态导数曲线Fig.

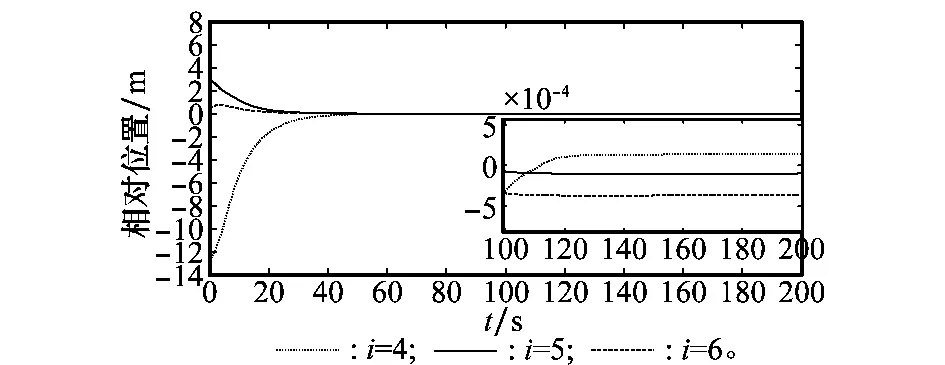
图7 相对位置re曲线Fig.7 Curves of relative position re

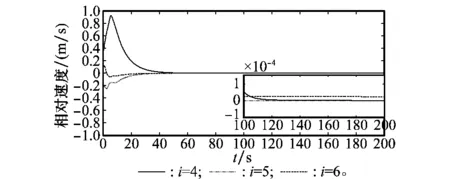
图8 相对速度ve曲线Fig.8 Curves of relative velocity ve

从图9和图10可以看出,初始的控制力矩u和控制力f比较大,但随着位置跟踪和姿态同步的逐步完成,u和f快速减小;由于控制器是连续的,因此不存在抖振现象 。

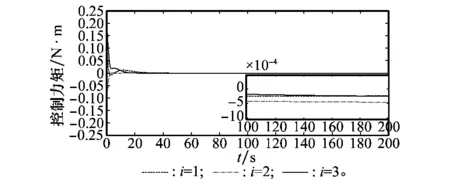
图9 控制力矩u曲线Fig.9 Curves of control torque u

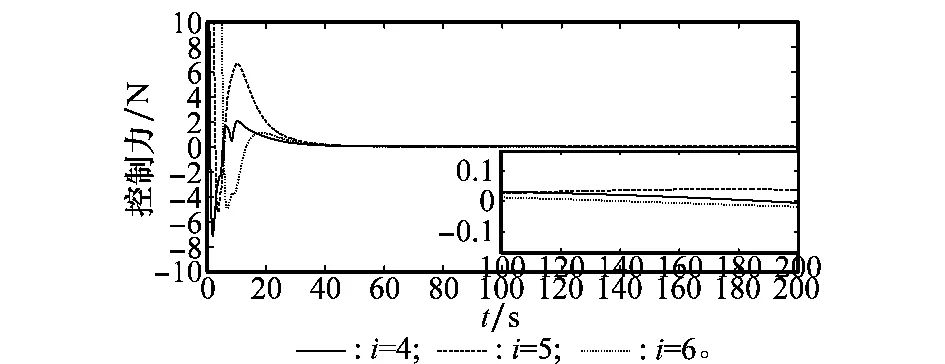
图10 控制力f曲线Fig.10 Curves of control force f

图11和图12为扰动力矩和扰动力估计曲线,可以看出自适应律式(35)估计出了dτ和df的界限,虽然估计值不会最终趋近于它们的真实值,但估计的误差值是有界的,因此可以满足有效抑制外部扰动的要求。

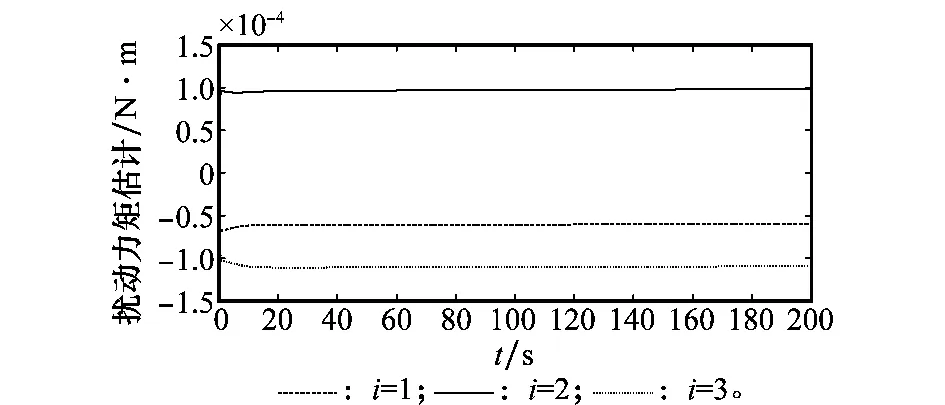
图11 扰动力矩dτ估计曲线Fig.11 Curves of disturbance torque dτ

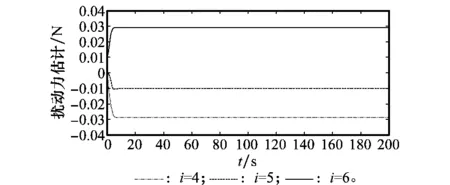
图12 扰动力df估计曲线Fig.12 Curves of disturbance force df

进一步地,为了验证总结2,控制器式(34)选取较小的增益矩阵,其他参数保持不变。

图13～图16为对应的系统响应曲线,与图5～图8对比可知,在一定范围内,控制增益越小,系统响应时间会越长,稳态误差会越大;但此时系统的有限时间收敛性和稳定性并没有改变,这说明了本文控制器的鲁棒性和有效性。

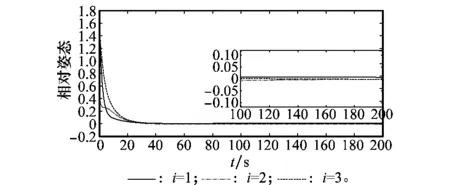
图13 相对姿态σe曲线(小增益)Fig.13 Curves of relative attitude σe (small gain)

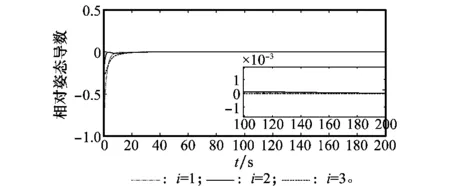
图14 相对姿态导数曲线(小增益)Fig.

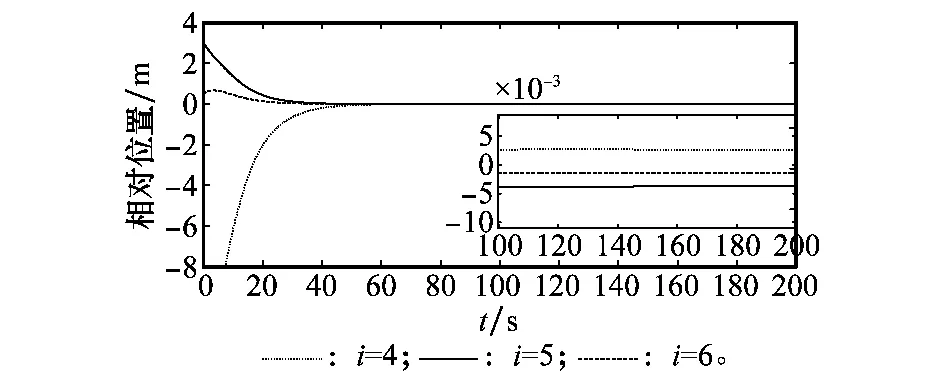
图15 相对位置re曲线(小增益)Fig.15 Curves of relative position re (small gain)

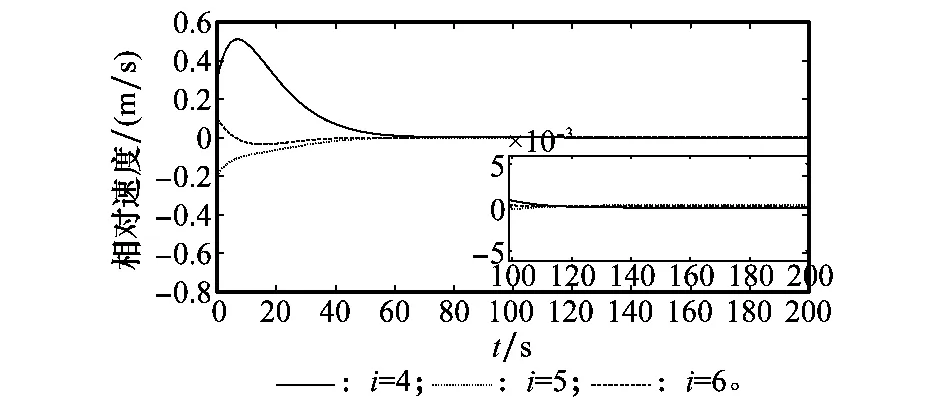
图16 相对速度ve曲线(小增益)Fig.16 Curves of relative velocity ve (small gain)

从仿真结果可知,采用本文设计的控制器,在有限时间内可实现气浮台追踪器对气浮台目标器姿态和位置的高精度跟踪。

5 结 论

本文基于交会对接地面物理仿真系统模拟卫星交会对接过程,在考虑姿态和位置动力学耦合作用以及外部扰动的情况下,采用快速非奇异终端滑模控制和自适应控制提出了一种鲁棒有限时间姿态位置耦合控制方法。该控制器保证了闭环系统是有限时间稳定的。仿真结果进一步表明了控制策略的有效性。

[1] Lin L X. Space rendezvous and docking technology[M].Beijing:NationalDefenceIndustryPress, 1995. (林来兴. 空间交会对接技术[M]. 北京: 国防工业出版社, 1995.)

[2]SaulnierK,PérezD,HuangRC,etal.Asix-degree-of-freedomhardwarein-the-loopsimulatorforsmallspacecraft[J]. Acta Astronautica, 2014, 10(27): 444-462.

[3]WuYH,GaoY,LinJW,etal.Low-cost,high-performancemonocularvisionsystemforairbearingtableattitudedetermination[J]. Journal of Spacecraft and Rockets, 2014, 51(1): 66-75.

[4]SunL,HuoW.Robustadaptiverelativepositiontrackingandattitudesynchronizationforspacecraftrendezvous[J]. Aerospace Science and Technology, 2015,41(1):28-35.

[5]YangJ,ShiXP.Integrityfaulttolerantattitudecontrollerofsatellitewithdisturbanceattenuation[J]. Systems Engineering and Electronics, 2013, 35(1): 126-131. (杨婧, 史小平. 卫星姿态系统的抗干扰完整性容错控制[J]. 系统工程与电子技术, 2013, 35(1): 126-131.)

[6]BaiH,ArcakM,WenJT.Rigidbodyattitudecoordinationwithoutinertialframeinformation[J]. Automatica, 2008, 44(12):3107-3175.

[7]LiuXM,ChengK.Flexiblesatelliteattitudecontrolbasedonoptimalswitchingalgorithm[J]. Systems Engineering and Electronics, 2014, 36(11): 2244-2248. (刘小梅, 程康. 基于最优切换的挠性卫星的姿态控制[J]. 系统工程与电子技术, 2014, 36(11): 2244-2248.)

[8]YangX,GaoH,ShiP.Robustorbitaltransferforlowearthorbitspacecraftwithsmall-thrust[J]. Franklin, 2010, 347(10):1863-1887.

[9]GaoX,TeoKL,DuanGR.Anoptimalcontrolapproachtorobustcontrolofnonlinearspacecraftrendezvoussystemwithθ-Dtechnique[J]. International Journal of Innovative Computing, Information & Control, 2013, 9(5): 2099-2110.

[10]ParkJU,ChoiKH,LeeS.Orbitalrendezvoususingtwo-stepslidingmodecontrol[J]. Aerospace Science Technology, 1993,9(4): 239-245.

[11]XinM,PanH.Indirectrobustcontrolofspacecraftviaoptimalcontrolsolution[J]. IEEE Trans.on Aerospace Electronic System, 2012, 48 (2): 1798-1809.

[12]SinglaP,SubbaraoK,JunkinsJL.Adaptiveoutputfeedbackcontrolforspacecraftrendezvousanddockingundermeasurementuncertainty[J]. Guidance Control Dynamics, 2006, 29(4): 892-902.

[13]ZhangF,DuanGR.Integratedtranslationalandrotationalfinite-timemaneuverofarigidspacecraftwithactuatormisalignment[J].IET Control Theory and Applications,2012,6(9):1192-1204.

[14]DuHB,LiSH.Finite-timeattitudestabilizationforaspacecraftusinghomogeneousmethod[J]. Journal of Guidance, Control, and Dynamics, 2012, 35(3): 740-748.

[15]HuoX,HuQ,XiaoB.Finite-timefaulttolerantattitudestabilizationcontrolforrigidspacecraft[J]. Isa Transactions, 2014, 53(2): 241-250.

[16]HuangC,ChenXL,WangY,etal.Rendezvousanddockingsimulationandattitudetrackingcontrolbasedonair-bearingtable[J]. Journal of Chinese Inertial Technology,2016,230(1): 172-188. (黄成, 陈兴林, 王岩,等. 基于气浮台的交会对接模拟及姿态跟踪控制[J]. 中国惯性技术学报, 2016, 230(1): 172-188.)

[17]GuoY,SongSM,YanZB.Finite-timecoordinationcontrolforformationflyingspacecraftwithoutunwinding[J]. Journal of Aerospace Engineering, 2015: 1-17.

Relative attitude and position control for rendezvous and docking based on air-bearing tables

HUANG Cheng, WANG Yan, CHEN Xing-lin

(DepartmentofControlScienceandEngineering,HarbinInstituteofTechnology,Harbin150001,China)

The problem of relative attitude and position control involved in satellite rendezvous and docking is studied based on a physical ground simulation system for rendezvous and docking. Based on the structure of the physical ground simulation system, the coupled 6 degrees of the freedom dynamics model is developed to describe the motion of the system, and then based on the proposed model, a robust finite-time control scheme is designed by using an adaptive fast non-singular terminal sliding mode control method, the controller can overcome the singularity problem of the traditional terminal sliding mode control under the disturbed condition. Lyapunov theory and simulation results show that the proposed controller can guarantee the finite-time stability and convergence of the system, meanwhile, it can effectively restrain external bounded disturbances.

air-bearing table;six degrees of freedom coupling;rendezvous and docking;terminal sliding mode;adaptive control

2016-02-22;

2016-10-18;网络优先出版日期:2016-11-22。

国家自然科学基金(61174037)；国家自然科学基金创新群体项目(61321062)资助课题

V 412.4

A

10.3969/j.issn.1001-506X.2016.12.20

黄 成(1986-),男,博士研究生,主要研究方向为高精度运动控制、气浮台姿态控制。

E-mail:huangchengsunxi@163.com

王 岩(1972-),男,教授,博士,主要研究方向为高精度先进运动控制技术、挠性航天器的姿态控制技术、智能控制及优化方法。

E-mail:yanw@hit.edu.cn

陈兴林(1963-),男,教授,博士,主要研究方向为高精密伺服系统、智能机器人、计算机控制、信号处理。

E-mail:chenxl@hit.edu.cn

网络优先出版地址:http://www.cnki.net/kcms/detail/11.2422.TN.20161122.1329.004.html