窄带雷达频谱混叠微动信号的平动补偿

王 超, 文树梁, 叶春茂

(北京无线电测量研究所, 北京 100854)



窄带雷达频谱混叠微动信号的平动补偿

王 超, 文树梁, 叶春茂

(北京无线电测量研究所, 北京 100854)

针对存在频谱混叠的窄带雷达微动信号平动补偿问题,从高阶和低阶频谱混叠两种情况出发,给出了一种平动补偿方法。在对两种频谱混叠情况分析的基础上,针对高阶混叠将混叠的瞬时频率近似为线性调频锯齿波信号,通过对频率以及调频率的估计,实现信号混叠程度的快速降阶。对于低阶混叠,首先将时频图在频率维周期扩展,再基于形态学图像处理方法提取出无模糊的瞬时频率曲线,最后对其进行多项式的最小二乘拟合完成平动补偿。仿真实验验证了所提方法的有效性以及对不同的信号形式和噪声的鲁棒性。

微动; 平动补偿; 频谱混叠

0 引 言

微动目标产生的微多普勒特征可用于对复杂目标的分类、识别和成像等领域[1-3]。对于微动目标的分析,人们通常将视线集中在特征提取方面,并假设目标没有平动或平动已经补偿[4-6]。在处理实际问题时,目标平动带来的影响往往不能忽略,因此平动补偿问题难以避免。国内外在该方面已有一部分成果,但仍显不够,下面进行简要总结。

文献[7-8]针对宽带雷达的距离-慢时间像提出了基于经验模式分解(empirical mode decomposition, EMD)的平动补偿方法。具体做法是将距离-慢时间像中多个“倾斜的”正弦曲线分解到不同的本征模态函数(intrinsic mode function, IMF)中,通过去除分解余量实现了有效的平动补偿。但对于窄带雷达时频(time-frequency, TF)曲线的平动补偿,这类方法可能因频谱混叠问题而失效。文献[9-10]将微动回波信号视为附加了正弦调频的多项式相位信号(sinusoidal frequency modulation-polynomial phase signal, SFM-PPS),利用高阶模糊函数(high-order ambiguity function,HAF)实现了多项式相位项的补偿。这类参数化方法对时域信号直接进行处理,不受频谱混叠的影响且具有一定的抗噪性能,但仅适合处理单分量信号,在多分量时将产生交叉项干扰。另一类常用的平动补偿方法是以频谱最小熵或最小频谱宽度为准则,对加速度、加加速度等平动参数直接进行搜索得到参数的估计值[11-12]。这类方法不考虑频率的瞬时状态,而将重点放在整体的聚集程度上,因此对不同的信号形式以及噪声具有更强的鲁棒性。但这类方法的补偿精度通常不高,且计算复杂度与补偿精度对搜索间隔与范围很敏感,在没有先验知识的情况下合理设置这些参数将变得很困难。

本文针对存在频谱混叠的窄带雷达微动信号平动补偿问题,首先依据混叠的程度分为高阶和低阶两种情况。对于高阶混叠,通过将混叠的瞬时频率近似为线性调频(linear frequency modulation, LFM)锯齿波信号,提出了一种快速降阶方法;对于低阶混叠,在频率维周期扩展的时频图上基于形态学图像处理给出了一种无模糊瞬时频率提取及平动补偿方法。所提方法对目标的运动形式以及噪声有较好的鲁棒性,且参数设置简单。

1 微动回波信号的两种频谱混叠情况

微动目标相对雷达的运动可分为平动和转动,则不同时刻目标相对雷达的距离可表达为

r(tm)=rT(tm)+rR(tm)

(1)

式中,tm为慢时间;rT(tm)为距离的平动分量;rR(tm)为距离的转动分量。

为简化问题而又不失一般性,假设目标的平动由速度、加速度和加加速度组成,则距离的平动分量可表达为

(2)

式中,r0为目标与雷达的初始距离;v为平动速度;a为平动加速度;g为平动加加速度。

对于单散射点的旋转运动,产生的距离分量可表示为

rR(tm)=Lksin(2πfotm+φk)

(3)

式中,Lk为散射点旋转幅度;fo为旋转频率;φk为旋转初相角。

对应的无模糊瞬时多普勒频率可表达为

(4)

式中,λ为雷达波长;fT(tm)为瞬时平动频率;fR(tm)为瞬时转动频率;Ak=4πf0Lk/λ为转动频率的幅度。

对于窄带微动信号,假设没有发生越距离单元徙动,则在目标所在的距离单元上利用时频分析方法(未作特殊说明则默认采用短时傅里叶变换)可获得混叠的二维时频像X(tm,f)。定义时频峰值曲线为

(5)

相应的峰值差分序列为

(6)

式中,fr为脉冲重复频率(pulse repetition frequency,PRF)。

图1表示出了两种典型的频谱混叠情况。

(1) 高阶频谱混叠:回波瞬时频率变化剧烈且呈现明显的周期性跳变,如图1(a)～图1(c)。

(2) 低阶频谱混叠:回波的瞬时频率整体相对变化缓慢,观察时间内只会跨越较少几个脉冲重复频率,如图1(d)～图1(f)。

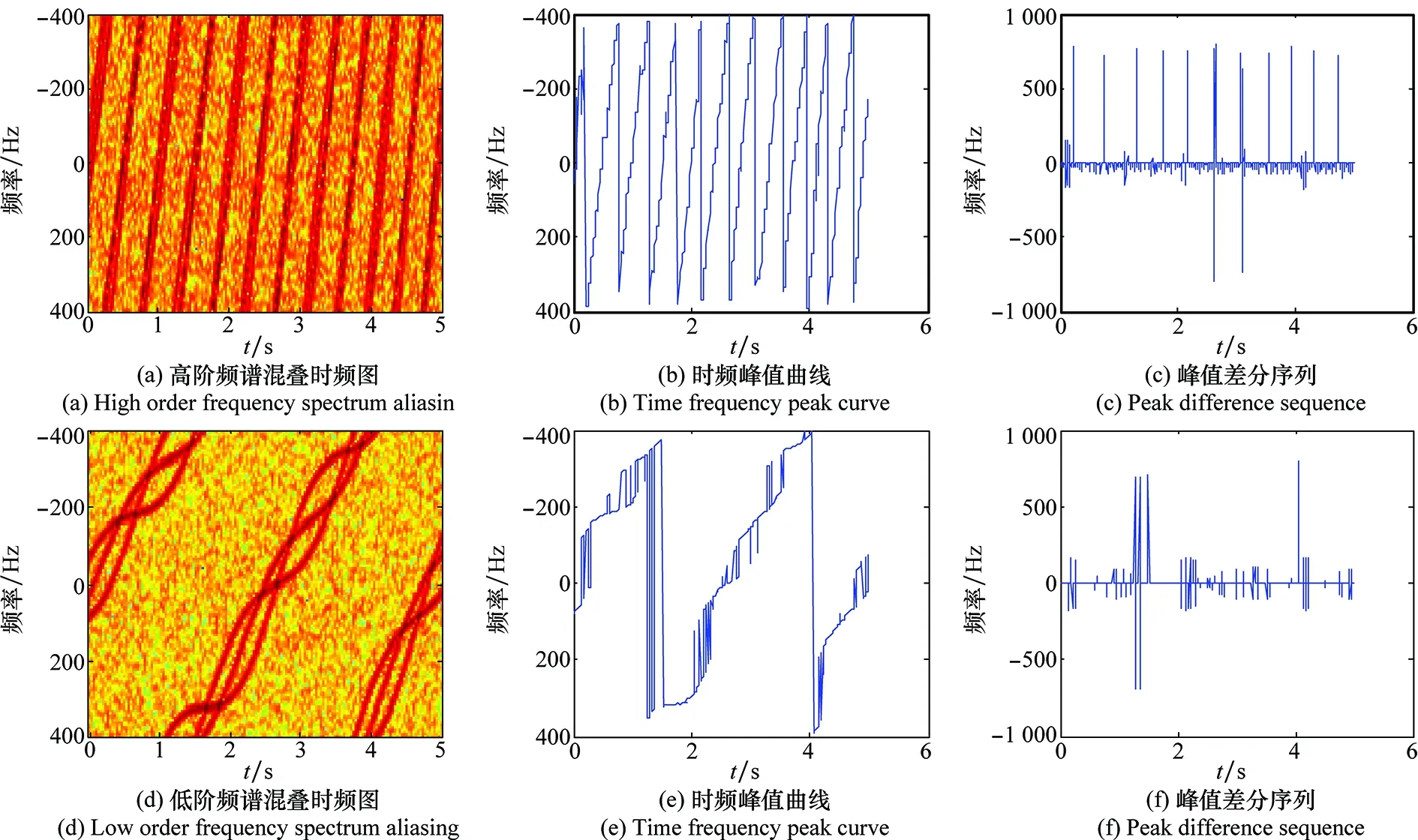
图1 频谱混叠示意图Fig.1 Spectrum aliasing scheme

从图1(a)和图1(b)中可发现,高阶频谱混叠的回波时频峰值曲线基本由平动表征。由于以PRF为间隔被周期性的截断,而在峰值差分序列中产生周期性的峰值,如图1(c)。而低阶频谱混叠的回波时频峰值曲线由平动和转动共同表征,如图1(d)和图1(e)。此时峰值差分序列不再显示出明显的周期性,如图1(f)。但相比于高阶频谱混叠,低阶的混叠现象仅出现在相邻的少数几个PRF内。

2 频谱混叠微动信号的平动补偿

对于频谱混叠的窄带雷达微动信号,首先进行无模糊瞬时频率的提取,再基于无模糊瞬时频率趋势项的最小二乘拟合实现平动补偿。当微动回波信号出现高阶频谱混叠时,需先进行预处理将信号降为低阶甚至无频谱混叠的情况。

对于无越距离单元徙动的窄带多分量微动信号,假设多个转动分量的幅度Ak都相对PRF较小,且微动信号的不同分量在时频面上是相交的。

2.1 高阶频谱混叠的快速降阶方法

在高阶频谱混叠情况下,模糊的时频峰值曲线主要由共同的平动加速度a和加加速度g表征,而多个转动分量可视为附加在平动项上的“伪随机噪声”ε(tm)。此时,无模糊的时频峰值曲线可表达为

(7)

受到信号回波PRF的限制,实际的时频峰值曲线可近似为锯齿波,具有如下形式：

(8)

式中,f0为锯齿波信号fsw(tm)基频分量的频率。

由式(8)可知,锯齿波的各次谐波分量能量依次递减。这里我们仅考虑最强分量,即基频分量。在时频像中,锯齿波基频频率f0相当于峰值曲线fpk(tm)变化一个PRF所需要的时间,即

(9)

式中,f′(·)为求导运算。

基于式(9),当加加速度为g=0时

(10)

因此,fsw(tm)的最强分量为一单频信号,其频率与目标平动加速度a相对应。

而当加加速度g≠0时,有

(11)

此时,基频信号的频率具有线性调频的形式。我们熟悉的LFM信号是正弦包络的,而这里fsw(tm)相当于锯齿波包络的LFM信号,在时频域其最强分量对应一条具有一定斜率的斜线。

综上所述,当加加速度g=0时,平动加速度的估计相当于频域的谱峰估计问题,可直接利用FFT求峰值或其他更高精度的估计方法;当加加速度g≠0时,平动加速度和加加速度的估计相当于LFM信号初始频率与调频率的估计问题,可利用基于时频面的Radon-Wigner变换或基于乘积型高阶模糊函数(product high-order ambiguity function,PHAF)的参数化估计方法。基于加速度、加加速度的估值进行平动的初次补偿即可实现降阶。由于平动速度仅会使瞬时频率产生一个恒定的偏移量,这里采用一个简单的圆移位实现补偿[13]。

2.2 时频面扩展

当信号为低阶混叠时,为恢复瞬时频率的连续性先将混叠的时频图进行正负方向的周期重复,得到扩展的时频图Xex(tm,f)。这里基于峰值差分序列来确定重复周期数

num+=Num{tm|Δfpk(tm)<-α·fr}

(12)

num-=Num{tm|Δfpk(tm)>α·fr}

(13)

式中,num+为正频率上重复的周期数;num-为负频率上重复的周期数;Num{.}为集合中的元素个数;α为接近但小于1的数,这里为了减小峰值频率在多分量间跳变的影响而引入。实际情况中,还可对差分序列中的峰值最小间隔Δtmin或最小正负向扩展周期数nmin进行设定。

2.3 无模糊瞬时频率提取

首先,将扩展的时频图进行二值化,可得

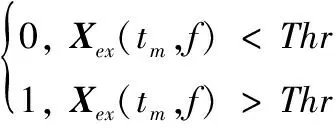
(14)

式中,Thr为二值化门限。

变换后的时频图Xex2(tm,f)可视为一幅二值化图像,利用数字图像处理的知识可实现噪声环境下连续瞬时频率曲线的提取。下面给出将用到几种特殊的形态学图像处理方法的表达式,具体说明参见文献[14],这里不再赘述。

(1) 开操作

用结构元素B对集合A进行开操作可表达为

A∘B=(A⊙B)⊕B

(15)

式中,A⊕B为结构元素B对集合A的膨胀操作;A⊙B为相应的腐蚀操作。

(2) 连通区域提取

令Y是包含于集合A中的连通分量,并假设Y中一点p是已知的,则连通分量可用下面的表达式迭代的得到:

Xk=(Xk-1⊕B)∩A,k=1,2,3…

(16)

式中,X0=p;B为一个适当大小的结构元素。当Xk=Xk-1时,迭代终止;Y=Xk即为提取出的连通分量。

当存在噪声时,在二值化的扩展时频图中将出现个别离散的小区域,并且信号瞬时频率曲线也将出现“毛刺”。开操作可使对象的轮廓变得光滑,消除细长的突出物。为了剔除“毛刺”并避免与邻近的噪声区域错误连接,这里先对图像进行一次开操作,再由混叠时频图中幅度最强点出发进行连通区域提取来实现无模糊瞬时频率的提取。其处理过程可表达为

Xda2=(Xk-1⊕B2)∩(Xex2∘B1)

(17)

式中,Xda2为无混叠的二值化时频图;B1为开操作中用到的结构元素;B2为连通分量提取时用到的结构元素。

将二值化时频图视为一个模板,可将扩展时频图中一条完整而无模糊的时频曲线提取出来

Xda=Xda2·Xex

(18)

2.4 基于无模糊瞬时频率的平动补偿

对于无模糊瞬时频率的平动补偿,可将Xda按行求重心作为多分量信号的平均瞬时频率fme(tm),并对其采用基于最小二乘(least square, LS)的二次多项式拟合来实现补偿。即

fme=D0·x+ε

(19)

式中

fme=(fme(t1),…,fme(tn))T

x=(v,a,g)T,ε=(ε(t1),…,ε(tn))T

需要指出的是,若得到的无混叠瞬时频率可近似为单个正弦信号与多项式信号的和信号,采用文献[15]中的方法能在提高补偿精度的同时实现正弦信号周期的估计。

3 实验仿真与分析

3.1 高阶频谱混叠的快速降阶

假设目标围绕中心点做二维转动,以中心点为圆心,转动平面为XOY面建立目标坐标系,目标中包含的3个分量在目标坐标系中的坐标分别为(0,1,0),(-1.2,0,0),(1.5,0,0)。平动加速度a=75.8 m/s2,加加速度g=5.45 m/s3,这里不考虑速度的影响,因此令平动速度v=0 m/s。同时,目标进行二维转动,对应的转动频率为frot=0.5 Hz。雷达的仿真参数有载频fc=3 GHz,脉冲重复频率fr=800 Hz,雷达视线对应的单位方向矢量为nradian=(0.5,-0.866,0),仿真时间T=5 s,信噪比(signal to noise ratio, SNR)SNR=10 dB。

此时,信号的时频图、时频峰值曲线和峰值差分序列如图1(a)～图1(c)所示。将时频峰值曲线做Wigner-Ville变换,如图2所示。观察图2可知,在时频面中时频峰值曲线可近似表征为一组平行的“斜线”,且强度随频率的增加依次递减,与之前锯齿波包络LFM信号的时频特征相符。

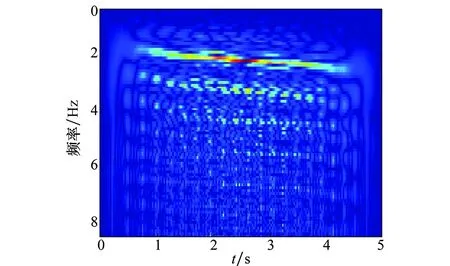
图2 高阶频谱混叠时频峰值曲线时频图Fig.2 TF distribution of TF peak curve with high-order spectrum aliasing

图3给出了基于本文的快速降阶方法得到的平动初步补偿结果。从图中可知,通过降阶方法去除了信号由平动造成的频谱混叠,且处理时间仅需要1.5 s。这里平动加速度、加加速度的估计方法采用PHAF。

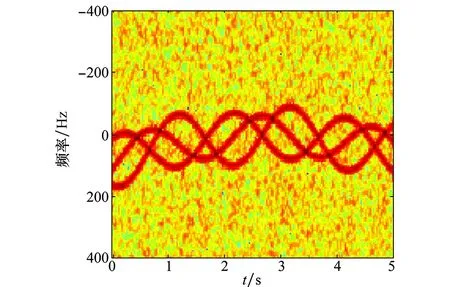
图3 高阶频谱混叠的快速降阶Fig.3 Fast degrade of high-order spectrum aliasing

3.2 低阶频谱混叠的平动补偿

令平动加速度a=13.4 m/s2,加加速度g=1.24 m/s3,则仿真时间内信号的频谱混叠将由高阶变为低阶,信号的时频图、时频峰值曲线和峰值差分序列如图1(d)～图1(f)所示。由峰值差分序列可得到负频率扩展周期数为3,正频率扩展周期数为1,其中α=0.8,Δtmin=T/20,nmin=1。扩展后的时频图如图4所示。将扩展时频图二值化,并利用形态学图像处理提取出的无模糊信号时频曲线如图5所示。其中,二值化门限取0.1倍时频图最大值,若时频图换算成了dB值则为最大值-10 dB。采用的结构元素为B1=ones(3,3),B2=ones(11,11),ones(n1,n2)为n1行、n2列值全为1的矩阵。无模糊的信号时频曲线的重心线如图6所示,它能对平动产生的趋势项进行有效近似。

图4 扩展时频图Fig.4 Expanded TF distribution

图5 无模糊时频曲线提取Fig.5 TF curve without frequency ambiguity

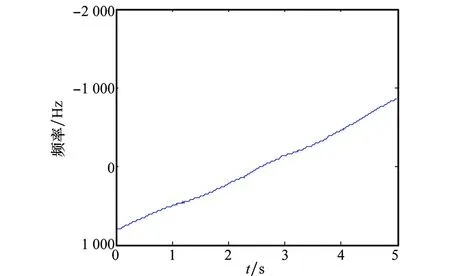
图6 时频曲线重心线Fig.6 Center line of TF curve

图7 低阶频谱混叠的补偿结果Fig.7 Compensate result of low-order spectrum aliasing

3.3 平动补偿方法的鲁棒性分析

本文提出的频谱混叠下的平动补偿方法对不同的信号形式以及噪声具有较好的鲁棒性。下面,从SNR和大转动分量两方面对该方法的鲁棒性进行分析。

3.3.1 信噪比

在之前高/低阶频谱混叠的仿真场景下,将SNR从10 dB降低到3 dB和-3 dB,得到的平动参数估计值示于表1中。从表中数据可知,本方法对噪声具有较好的鲁棒性。

高阶频谱混叠时噪声的影响等价于时频峰值曲线的锯齿波近似中噪声项ε(tm)的增加。由于PHAF对噪声有较好的鲁棒性,因而在SNR较低时仍能实现有效的降阶。对于低阶频谱混叠时,图8显示出了3 dB SNR下开操作对二值化图像的去噪效果。可发现,开运算不仅能滤除小的噪声斑,还能增加剩余噪声彼此或与信号间的离散度,与相互连通的信号分量呈现两种不同的状态。基于此,可实现无模糊时频曲线的重心线提取,如图9所示。通过与图6对比可发现,随着SNR的降低提取出的重心线产生了“毛刺”。

表1 不同SNR下平动参数估计结果

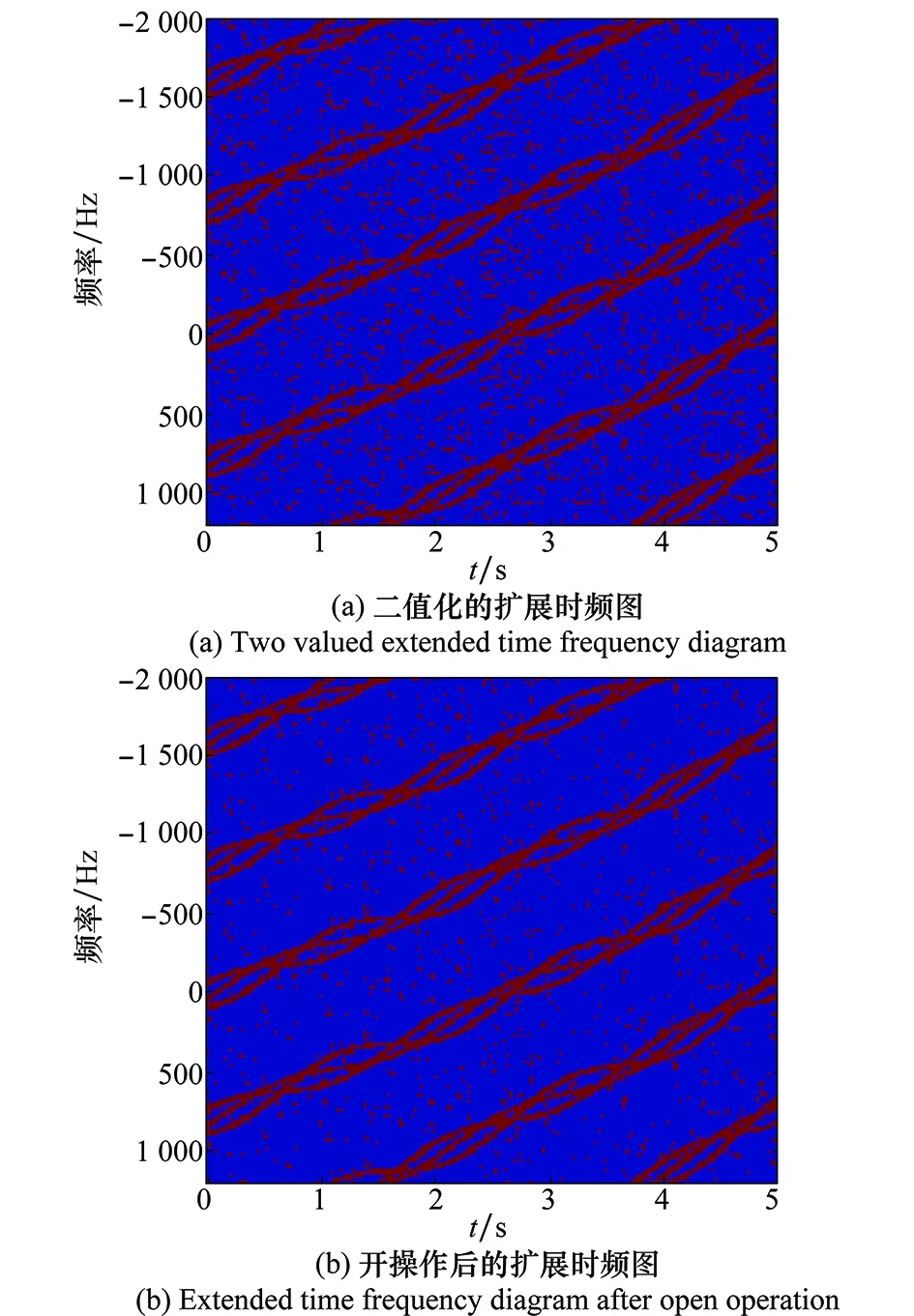
图8 开操作去噪Fig.8 Denoising with open operation

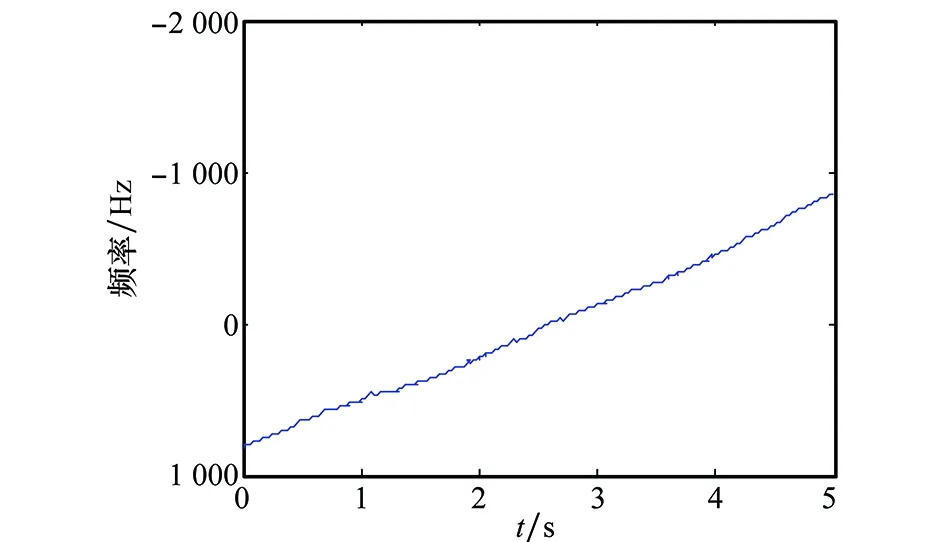
图9 无模糊时频曲线的重心线Fig.9 Center line of TF curve without frequency ambiguity

3.3.2 特殊信号形式—单个大转动分量

转动产生的频率变化受到分量在目标坐标系中的位置、雷达波长以及转速的影响。这里将单个信号分量的坐标设为(0,10,0),其他参数同第3.2节,则转动频率的幅度Ak将超过1倍PRF,如图10所示。采用低价频谱混叠平动补偿方法,由重心近似的瞬时频率曲线如图11所示。

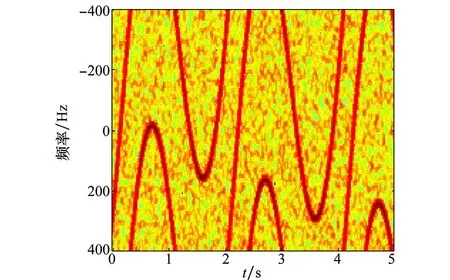
图10 单个大转动分量的时频图Fig.10 TF distribution of single component with large frequency variation

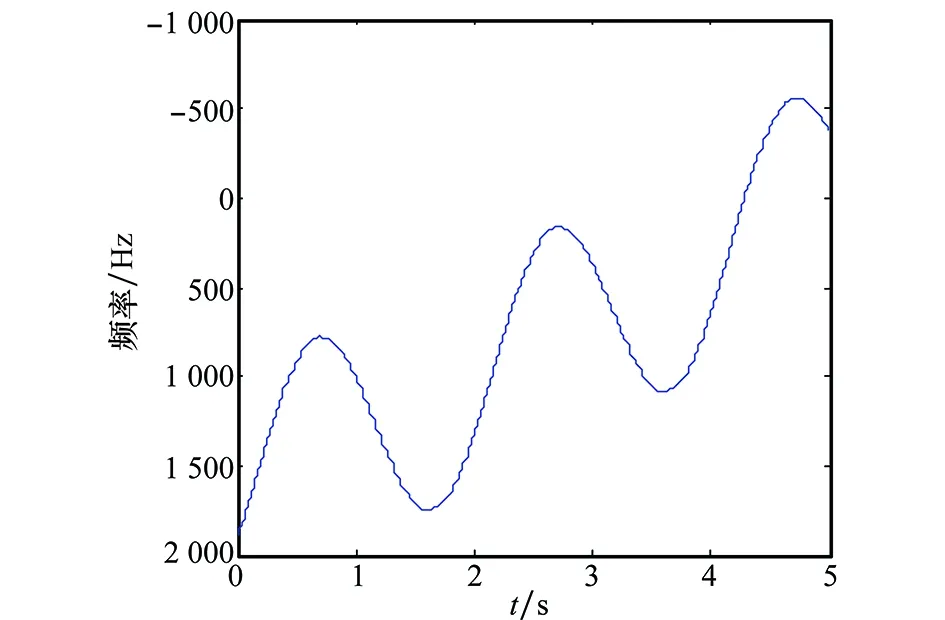
图11 提取的重心线Fig.11 Extracted center line

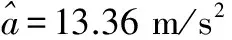
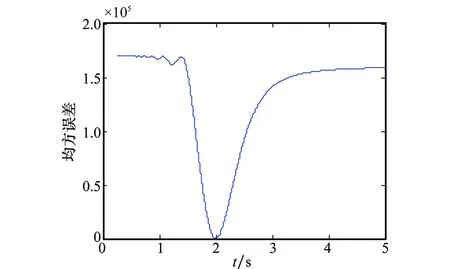
图12 最小二乘均方误差与周期的关系曲线Fig.12 Relation curve between LS mean square error and rotate period

值得注意的是,大转动分量情况下基于最小熵的平动补偿将不再适用,其补偿结果如图13所示。其中,加速度搜索范围为-100～100m/s2,均匀搜索800点,加加速度搜索范围为-20～20m/s3,均匀搜索400点。

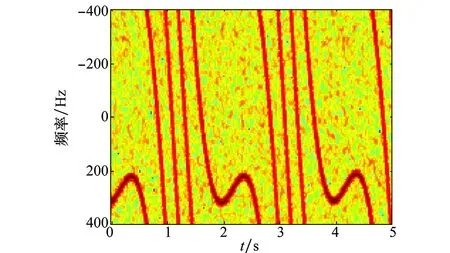
图13 基于最小熵的大转动分量平动补偿结果Fig.13 Translational compensation result based on minimum entropy

4 结 论

本文针对窄带雷达频谱混叠微动信号的平动补偿问题,从高阶和低阶频谱混叠两种情况出发,给出了一种无模糊瞬时频率提取及平动补偿方法。提出的方法对噪声以及一些特殊的信号形式具有较好的鲁棒性。基于提取出的无模糊瞬时频率,本方法也可以与已有的一些针对无模糊情况的平动补偿方法联合使用,如之前提到的基于EMD的平动补偿方法。

值得指出的是,为了简化问题,本文采用了点目标的仿真模型。它能较好的表征弹道类等具有简单散射特性的目标。而针对电磁散射特性更为复杂的目标,由于时频面重心线通常能够表征平动引起的整体趋势变化,因此保证了算法的有效性。

[1]ChenVC,LiF,HoSS,etal.Micro-Dopplereffectinradar:phenomenon,modelandsimulationstudy[J]. IEEE Trans.on Aerospace and Electrical System, 2006, 42(1): 2-21.

[2]LuoY,ZhangQ,QiuCW,etal.Micro-DopplereffectanalysisandfeatureextractioninISARimagingwithstepped-frequencychirpsignals[J]. IEEE Trans.on Geoscience and Remote Sen-sing, 2010, 48(4): 2087-2098.

[3]MaL,LiuJ,WangT,etal.Micro-Dopplercharacteristicsofsliding-typescatteringcenteronrotationallysymmetrictarget[J]. Science in China Scientia Sinica Information Sciences,2011,41(5):605-616.

[4]SunHX,LeiZ.Nutationfeatureextractionofballisticmissilewarhead[J]. Electronics Letters, 2011, 47(13):770-772.

[5]LeiP,WangJ,SunJ.Analysisofradarmicro-Dopplersignaturesfromrigidtargetsinspacebasedoninertialparameters[J]. IET Radar Sonar Navigation, 2011, 5(3): 93-102.

[6]StankvicL,DjurovicI,ThayaparanT.Separationoftargetrigidbodyandmicro-DopplereffectsinISARimaging[J]. IEEE Trans.on Aerospace and Electrical System, 2006, 42(4):1496-1506.

[7]LuoY,BaiYQ,ZhangQ,etal.Translationalmotioncompensationandmicro-Dopplerfeatureextractionofballistictargets[J]. Journal of Electronics & Information Technology, 2012, 34(3):602-608.

[8]ZhaoYQ,WangGZ,BaiYQ,etal.AnewalgorithmoftranslationalcompensationforspacespinningtargetbasedonEMD[C]∥Proc.of IEEE International Conference on Signal Processing, Communications and Computing, 2013: 1-5.

[9]YangYC,TongNN,FengCQ,etal.Translationcompensationandmicro-Dopplerextractionoftheechofromballistictargetsinmidcourse[J]. Scientia Sinica(Informationis), 2013, 43(9):1172-1182.

[10]LiuJ.Radarsignalparameterestimationandphysicalfeatureextractionofmicro-motiontargets[D].Changsha:NationalUniversityofDefenseTechnology, 2010.(刘进.微动目标雷达信号参数估计与物理特征提取[D].长沙:国防科学与技术大学,2010.)

[11]YuWY,WangJF.Phaseadjustmentforextractionofmicro-motioninformationofballistictargets[C]∥Proc.of the IEEE International Congress on Image and Signal Processing, 2012: 1837-1840.

[12]GaoHW,XieLG,WenSL,etal.Researchontheinfluenceofaccelerationonmicro-Doppleranditscompensation[J]. Journal of Astronautics, 2009, 30(2): 705-711. (高红卫, 谢良贵,文树梁,等.加速度对微多普勒的影响及其补偿研究[J].宇航学报,2009,30(2):705-711.)

[13]GaoHW,XieLG,WenSL,etal.Researchontheinfluenceofvelocityonmicro-Doppleranditscompensation[J]. Aerospace Electronic Warfare, 2008, 24(4):46-50. (高红卫,谢良贵,文树梁,等.速度对微多普勒的影响及其补偿研究[J].航天电子对抗, 2008, 24(4):46-50.)

[14]ConzalezRC,WoodsRE. Digital image processing[M].YuanQT,trans. 2nded.Beijing:PublishingHouseofElectronicsIndustry,2006:423-437.(冈萨雷斯伍兹.数字图像处理[M].阮秋琦,译.2版. 北京:电子工业出版社,2006:423-437.)

[15]WuYH,YangJF,ChengJY,etal.Highaccuracyestimationalgorithmfor4parametersofsinewave[J].Journal of University of Science and Technology of China, 2006, 36(6):625-629.(吴义华,杨俊峰,程敬原,等.正弦信号四参数的高精度估计算法[J].中国科学技术大学学报,2006,36(6):625-629.)

Translational compensation of micro-motion with spectrum aliasing for narrow-band radar

WANG Chao, WEN Shu-liang, YE Chun-mao

(BeijingInstituteofRadioMeasurement,Beijing100854,China)

A translational compensation algorithm of micro-motion with spectrum aliasing for narrow-band radar is proposed. It is done in high-order and low-order spectrum aliasing cases. Based on the analysis of these two aliasing cases, the translational can be fast degraded by approximating the aliasing frequency as a linear frequency modulation saw-tooth wave in high-order spectrum aliasing cases. To deal with the low-order spectrum aliasing, the time-frequency image is expanded in frequency, and then the time-frequency curve without frequency ambiguity can be extracted based on morphological image processing. Finally, the least-square fitting of polynomial is utilized in the curve for translational compensation. Simulations are given to validate the effectiveness and robustness of the proposed algorithm.

micro-motion; translational compensation; spectrum aliasing

2015-12-24;

2016-08-08;网络优先出版日期:2016-08-22。

国家自然科学基金(61271417)资助课题

TN 95

A

10.3969/j.issn.1001-506X.2016.12.08

王 超(1990-),男,博士研究生,主要研究方向为雷达目标识别技术。

E-mail:whhitwa@126.com

文树梁(1971-),男,研究员,博士研究生导师,主要研究方向为雷达系统设计与信号处理。

E-mail:wenshul@sina.com

叶春茂(1981-),男,高级工程师,硕士研究生导师,主要研究方向为雷达ISAR成像与目标识别技术。

E-mail:danielgodman@163.com

网络优先出版地址:http:∥www.cnki.net/kcms/detail/11.2422.TN.20160822.1005.004.html