第七讲统计与概率

文/李培华

第七讲统计与概率

文/李培华

统计与概率是历年中考必考的重要内容．用统计知识解决实际问题是中考命题的重点．下面以2015年的中考题为例，把常见的考点归纳总结如下，供你复习时参考．

考点1普查与抽样调查

例1（2015年台州卷）在下列调查中，适宜采用全面调查的是（）．

A.了解我省中学生视力情况B.了解九（1）班学生校服的尺码情况

C.检测一批电灯泡的使用寿命D.调查台州《600全民新闻》栏目的收视率

解：选B.

温馨小提示：一般来说，对于具有破坏性的调查，无法进行普查、普查的意义或价值不大时，应选择抽样调查，对于精确度要求高的调查，事关重大的调查往往选用普查.

考点2不可能事件、随机事件、必然事件

例2（2015年徐州卷）一只不透明的袋子中装有4个黑球、2个白球，每个球除颜色外都相同，从中任意摸出3个球，下列事件为必然事件的是（）．

A.至少有1个球是黑球B.至少有1个球是白球

C.至少有2个球是黑球D.至少有2个球是白球

解：选A．

温馨小提示：理解必然事件、不可能事件、随机事件的概念是解题的前提.必然事件是指在一定条件下一定发生的事件.不可能事件是指在一定条件下，一定不发生的事件.不确定事件即随机事件是指在一定条件下，可能发生也可能不发生的事件.

考点3众数、中位数和平均数

例3（2015年宜昌卷）某校对九年级6个班学生平均一周的课外阅读时间进行了统计，分别为（单位：h）：3.5，4，3.5，5，5，3.5．这组数据的众数是（）．

A.3B.3.5C.4D.5

解：在这一组数据中3.5出现了3次，次数最多，故众数是3.5．选B．

例4（2015年广东卷）一组数据2，6，5，2，4，则这组数据的中位数是（）．

A.2B.4C.5D.6

解：将一组数据从小到大（或从大到小）重新排列后，最中间的那个数（或最中间两个数的平均数）称为中位数.将这组数据从小到大排序为2，2，4，5，6，∴中位数是4．选B.

考点4方差、标准差和极差

例5（2015年齐齐哈尔卷）某活动小组学生的年龄：13，15，15，16，13，15，14，15（单位：岁），这组数据的中位数和极差分别是（）.

A.15，3B.14，5C.16，16D.14，3

解：把这组数据从小到大排序：13，13，14，15，15，15，15，16.共8个数据，中位数是（15+15）÷2 =15，极差为16-13=3.选A.

例6（2015年湖州卷）已知一组数据的方差是3，则这组数据的标准差是（）.

解：根据“标准差=方差的算术平方根”可知，选D.

温馨小提示:方差用来衡量一批数据的波动大小（即这批数据偏离平均数的大小）.方差越大，说明数据的波动越大，越不稳定；反之，方差越小，数据越稳定.极差是这组数据的最大数与最小数的差.

考点5频数、频率与概率

例7（2015年本溪卷）在一个不透明的口袋中，装有若干个红球和4个黄球，它们除颜色外没有任何区别，摇匀后从中随机摸出一个球，记下颜色后再放回口袋中，通过大量重复摸球实验发现，摸到黄球的频率是0.2，则估计盒子中大约有红球（）．

A.16个B.20个C.25个D.30个

解：设红球有x个，根据题意得，4：（4+x）=1：5，解得x=16．选A．

温馨小提示：大量重复实验时，事件发生的频率在某个固定位置左右摆动，且摆动的幅度越来越小，可以用频率的集中趋势来估计概率，这个固定的近似值就是事件的概率.

考点6用样本估计总体

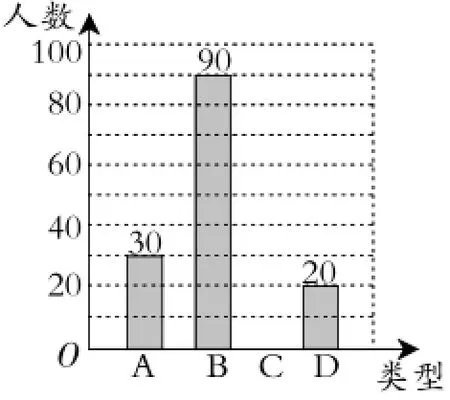
图1

例8（2015年盐城卷）2015年是中国人民抗日战争暨世界反法西斯胜利70周年，9月3日全国各地将举行有关纪念活动.为了解初中学生对二战历史的知晓情况，某初中课外兴趣小组在本校学生中开展了随机问卷调查，调查结果分为A、B、C、D四类，其中A类表示“非常了解”、B类表示“比较了解”、C类表示“基本了解”、D类表示“不太了解”，调查的数据经整理后形成下列尚未完成的条形统计图（如图1）和扇形统计图（如图2）.

根据正交试验结果得到的最优白藜芦醇脂质体处方。于DPPC脂质体水化时，分别加入含有与DPPC等质量比的乳糖、蔗糖、葡萄糖、海藻糖、甘露醇的PBS水化30 min，超声15 min，冷冻干燥48 h，得白藜芦醇DPPC脂质粉雾剂。以外观、色泽、再分散性为主要评价指标。外观以饱满、不塌陷、不皱缩、表面光洁为佳；色泽以均匀无花斑、质地细腻为佳；再分散性是加入纯化水后能在30 s内完全分散得脂质体为佳。优选甘露醇为白藜芦醇DPPC脂质粉雾剂载体（表3）。

（2）请把图1中的条形统计图补充完整；

（3）图2的扇形统计图中D类部分所对应扇形的圆心角的度数为°；

（4）如果这所学校共有初中学生1500名，请你估算该校初中学生中对二战历史“非常了解”和“比较了解”的学生共有多少名？

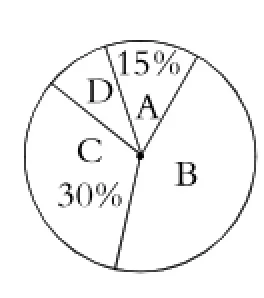
图2

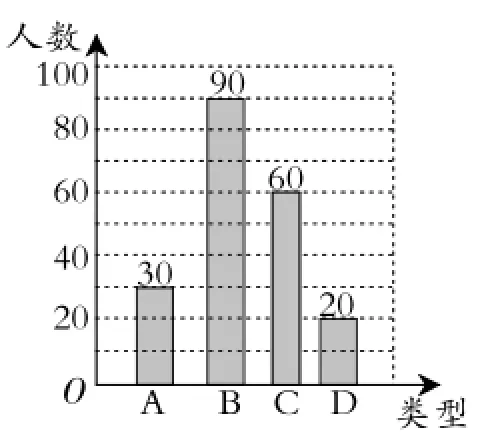
图3

解：（1）30÷15%=200.在这次抽样调查中，一共抽查了200名学生.（2）补充完整的条形统计图如图3所示.

（3）20÷200=0.1=10%.D类部分所对应扇形的圆心角为36°.

故对二战历史“非常了解”和“比较了解”的学生共有900名.

考点7概率的计算

例9（2015年长沙卷）一个不透明的袋子中只装有3个黑球，2个白球，这些球的形状、大小、质地等完全相同，即除颜色外无其他差别．在看不到球的条件下，随机从袋中摸出1个球，则摸出白球的概率是

温馨小提示：从若干元素中抽取一个元素（即一次操作问题）时，都可以直接应用公式P（A）（其中m表示事件A发生可能出现的结果数，n表示一次试验所有等可能出现的结果数）求概率.

责任编辑：王二喜