第五讲图形与变换

文/汪国刚

第五讲图形与变换

文/汪国刚

图形与变换是初中数学的重要内容，也是中考的重要考点．它包括图形的对称、平移、旋转、相似、位似等内容.现以2015年的中考题为例，把主要考点归纳如下，供你复习时参考．

考点1轴对称图形与中心对称图形的识别

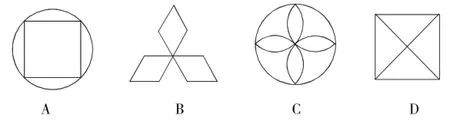
例1（2015年长沙卷）下列图形中，是轴对称图形，但不是中心对称图形的是（）．

解析：选B.

温馨小提示：判断轴对称图形的关键是寻找对称轴，使图形按照某条直线折叠后两旁部分可重合；判断中心对称图形的关键是寻找对称中心，使图形绕该中心旋转180°后与原图形重合.

考点2利用轴对称的性质计算

例2（2015年桂林卷）如图1，在△ABC中，AB=10，AC=8，BC=12，AD⊥BC于D，点E、F分别在AB、AC上，把△ABC沿EF折叠，使点A与点D恰好重合，则△DEF的周长是（）.

A.14B.15C.16D.17

解：设AD和EF的交点为M援

疫ΔEDF是ΔEAF折叠以后形成的图形，

亦ΔEDF的周长等于ΔEAF的周长，

由折叠知EF为△ABC的中位线，

温馨小提示：把ΔEDF的周长转化为ΔEAF的周长是解题的关键.另外，求最短路径问题，一般要考虑线段的性质定理，结合轴对称变换来解决，多数情况要作点关于某直线的对称点.

图1

图2

图3

图4

图5

考点3图形的平移

例3（2015年永州卷）在等腰△ABC中，AB=AC，则有BC边上的中线、高线和∠BAC的平分线重合于AD（如图2）援若将等腰ΔABC的顶点A向右平行移动后，得到ΔA忆BC（如图3），那么，此时BC边上的中线、BC边上的高线和∠BA忆C的平分线应依次分别是（填A忆D、A忆E、 A忆F）

解析：A忆D，A忆F，A忆E.

考点4旋转的性质及计算

例4（2015年福州卷）如图4，在Rt△ABC中，∠ABC越90°，AB越BC越将△ABC绕点C逆时针旋转60°，得到ΔMNC，连接BM，则BM的长是

解析：连接AM（如图5）.

∴△ACM是等边三角形，亦MC越MA，

又∵BC越BA，亦BM⊥AC.

温馨小提示：解此题的突破口是连接AM，结合旋转性质、等边三角形性质证明垂直是关键，进而由勾股定理求出相应线段即可.

考点5图形的轴对称、平移、旋转

例5（2015年张家界卷）如图6，在边长均为1的正方形网格纸上有一个△ABC，顶点A、B、C及点O均在格点上，请按要求完成以下操作或运算：

（1）将△ABC向上平移4个单位，得到ΔA1B1C1（不写作法，但要标出字母）；

（2）将△ABC绕点O旋转180°，得到△A2B2C（2不写作法，但要标出字母）；

（3）求点A绕着点O旋转到点A2所经过的路径长.

解析：（1）如图7所示．

（2）如图7所示.

（3）∵OA=4，∠AOA2=180°，

∴旋转经过的路径长为180仔×4=4仔. 180

温馨小提示：借助网格结构、平移距离、旋转角度找出对应点的位置是解题的关键.计算某点旋转经过的路线（弧线）长度，需要找出旋转角度、旋转半径，从而运用弧长公式计算.

图6

图7

考点6相似三角形

例6（2015年湘潭卷）如图8，在Rt△ABC中，∠C=90°，△ACD沿AD折叠，使得点C落在斜边AB上的点E处．

（1）求证：ΔBDE∽ΔBAC；

（2）已知AC=6，BC=8，求线段AD的长度．

解析：（1）∵∠C=90°，△ACD沿AD折叠，

∴∠C=∠AED=90°，∴∠DEB=∠C=90°，

∵∠B=∠B，亦ΔBDE∽ΔBAC.

（2）由勾股定理得，AB=10．

由折叠的性质知，AE=AC=6，DE=CD，∠AED=∠C=90°．

∴BE=AB-AE=10-6=4.

在Rt△BDE中，由勾股定理得，DE2+BE2=BD2，

即CD2+42=（8-CD）2，解得CD=3.

图8

在RtΔACD中，由勾股定理得AC2+CD2=AD2，

即32+62=AD2，解得AD=3

温馨小提示：此题涉及相似三角形的判定和性质，折叠是一种对称变换，它属于轴对称，根据轴对称的性质，折叠前后图形的形状和大小不变，对应边和对应角相等.一般需要运用勾股定理求解.

考点7位似

例7（2015年钦州卷）如图9，以O为位似中心，将边长为256的正方形OABC依次作位似变换，经第一次变换后得到正方形OA1B1C1，其边长OA1缩小为OA的，经第二次变换后得到正方形OA2B2C2，其边长OA2缩小为OA1的，经第三次变换后得到正方形OA3B3C3，其边长OA3缩小为OA2的，依次规律，经过第n次变换后，所得正方形OAnBnCn的边长为正方形OABC边长的倒数，则n=.

图9

正方形OAnBnCn的边长为×256.

∵正方形OAnBnCn的边长为正方形OABC边长的倒数，

温馨小提示：本题是以正方形为背景的规律探索题，根据前几次变换，得到相应正方形边长，经过归纳、猜想，发现第n次变换的边长，继而根据题意得到答案.

考点8相似三角形的应用

例8（2015年邵阳卷）某校数学兴趣小组利用自制的直角三角形纸板DEF测量操场旗杆AB的高度（图10），他们通过调整测量位置，使斜边DF与地面保持水平，并使边DE与旗杆顶点A在同一直线上，已知DE=0.5米，EF=0.25米，目测点D到地面的距离DG=1.5米，到旗杆的水平距离DC=20米，求旗杆的高度.

图10

∵DE=0.5米，EF=0.25米，DG=1.5米，DC=20米，

∴AB=AC+BC=10+1.5=11.5（米）.

答：旗杆的高度为11.5米.

温馨小提示：将实际问题转化为数学问题，运用相似三角形知识测量旗杆的高，发现△DEF∽ΔDCA是解题关键.

责任编辑：王二喜