第六讲图形与坐标

文/朱广科

第六讲图形与坐标

文/朱广科

责任编辑：王二喜

平面直角坐标系架起了数与形之间的桥梁，加强了知识之间的联系，为我们利用数形结合的思想提供了强有力的工具．图形与坐标多以选择题、填空题呈现．现将图形与坐标常考知识点分析如下，供你复习时参考．

考点1判断点所在象限

例1若点A（a+1，b-2）在第三象限，则点B（-a袁b-5）在（）．

A.第一象限B.第二象限C.第三象限D.第四象限

解：由A（a+1，b-2）在第三象限，得a+1＜0，b-2＜0，

解得a＜-1，b＜2．

由不等式的性质，得-a＞1，b-5＜-3，

点B（-a袁b-5）在第四象限．选D．

点评：掌握各个象限内点的坐标特征是解题的关键.第一象限内的点(+，+)；第二象限的点(-，+)；第三象限的点(-，-)；第四象限的点(+，-).

考点2对称点的坐标

例2在平面直角坐标系中，点A的坐标是（m，n），作点A关于x轴的对称点，得到点A忆，再作点A忆关于y轴的对称点，得到点A义，则点A义的坐标是（，）．

解：点A（m，n）关于x轴的对称点A忆的坐标为（m，-n），

点A忆（m，-n）关于y轴的对称点A义的坐标是（-m，-n）．

点评：关于x轴对称点的坐标，横坐标不变，纵坐标互为相反数；关于y轴对称点的坐标，横坐标互为相反数，纵坐标不变；关于原点对称点的坐标，横、纵坐标都互为相反数.掌握对称点的坐标特征是解答这类问题的关键.

考点3用坐标定位置

例3（2015年六盘水卷）观察中国象棋的棋盘，其中红方“马”的位置可以用一个数对（3，4）来表示，红“马”走完“马3进四”后到达B点，则表示B点位置的数对是：．

解：建立平面直角坐标系如图1所示，点B的坐标为（2，6）.

点评：借助于网格线，将点的位置数量化，找出表示位置的方法.解决问题的关键是确定原点，建立正确的坐标系，理解有序实数对与点的对应关系.

图1

考点4坐标与平移

例4（2015年济南卷）如图2，在平面直角坐标系中，△ABC的顶点都在方格纸的格点上，如果将△ABC先向右平移4个单位长度，再向下平移1个单位长度，得到△A1B1C1，那么点A1的对应点的坐标为（）．

A.（4，3）B.（2，4）C.（3，1）D.（2，5）

解：由坐标系可得A（-2，6），向右平移4个单位长度，再向下平移1个单位长度，点A的对应点A1的坐标为（-2+4，6-1），即（2，5）.选D．

点评：点向右（左）平移，横坐标相加（减），纵坐标不变；点向上（下）平移，纵坐标相加（减），横坐标不变.掌握点的平移与坐标变化的规律是解题的关键.

图2

考点5坐标与旋转

例5（2015年孝感卷）在平面直角坐标系中，把点P（-5，3）向右平移8个单位得到点P1，再将点P1绕原点旋转90°得到点P2，则点P2的坐标是（）．

A．（3，-3）B．（-3，3）

C．（3，3）或（-3，-3）D．（3，-3）或（-3，3）

解：∵把点P（-5，3）向右平移8个单位得到点P1（3，3），如图3所示，将点P1绕原点逆时针旋转90°得到点P2（-3，3），将点P1绕原点顺时针旋转90°得到点P3（3，原3）．选D．

图3

点评：明确旋转的性质，找出对应点的位置是解题的关键.本题由于没有明确旋转方向，所以要分类讨论，以防漏解.

考点6坐标与位似

例6（2015年武汉卷）如图4，在直角坐标系中，有两点A（6，3），B（6，0），以原点O为位似中心，相似比为，在第一象限内把线段AB缩小后得到线段CD，则点C的坐标为（）．

A.（2，1）B.（2，0）

C.（3，3）D.（3，1）

图4

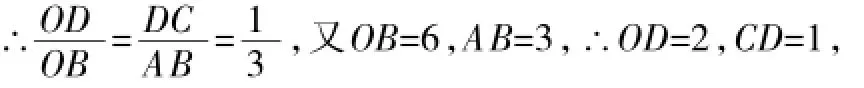
∴点C的坐标为（2，1）．选A．

点评：位似图形对应点的连线都经过位似中心，对应点到位似中心的距离之比等于位似比，图形的周长比等于位似比，面积比等于位似比的平方.

考点7坐标与规律探索

例7（2015年潜江卷）菱形ABCD在直角坐标系中的位置如图5，其中点A的坐标为（1，0），点B的坐标为，动点P从点A出发，沿A→B→C→D→A→B→……的路径，在菱形的边上以每秒0.5个单位长度的速度移动，移动到第2015秒时，点P的坐标为

图5

∵点P的速度为0.5米/秒，

∴沿A→B→C→D→A所需的时间4×4=16秒．

∴移动到第2015秒时，点P在AD上，且DP∶PA越3∶1，

点评：根据题意得出点P运动一周所需的时间是解题的关键.与坐标系有关的规律探究题成为近几年中考的热点，通过“形”的变化，探究“数”的变化，需要从特殊情况出发，通过分析、猜想或运算，归纳出一般性的结论.