第四讲图形的性质

文/陈昭能 周奕生

第四讲图形的性质

文/陈昭能 周奕生

图形的基本性质历来是中考命题的重点，掌握基本图形的性质是中考取得高分的前提，也是解决几何综合题的基础．图形性质的主要考点有：

考点1命题真假的判断

例1（2015年无锡卷）命题“全等三角形的面积相等”的逆命题是命题．（填入“真”或“假”）

分析：欲知该命题的逆命题的真假性，需确定它的逆命题：面积相等的三角形全等．这显然是假命题，故填“假”．

温馨小提示：判断一个命题的逆命题的真假性，关键在于正确写出原命题的逆命题，再判断逆命题是否正确.

考点2几何体与展开图

例2（2015年泰州卷）一个几何体的表面展开图如图1所示，则这个几何体是（）．

A.四棱锥B.四棱柱

C.三棱锥D.三棱柱

分析与解：根据经验，图1是四棱锥的表面展开图．选A.

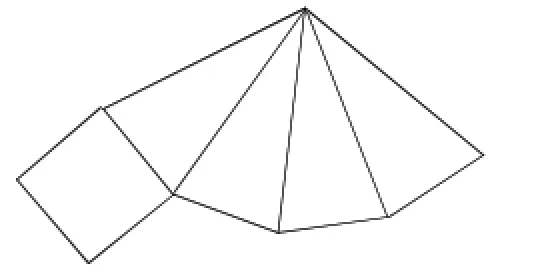
图1

例3（2015年恩施卷）图2是一个正方体纸盒的展开图，六个正方形上分别标有数字“0”、“1”、“2”、“5”和汉字“数”、“学”，将其围成一个正方体后，则与“5”相对的是（）．

A.0B.2C.数D.学

分析与解：相对面之间没有公共点，因此，与“5”相对的是0.选A.

温馨小提示：带图案正方体表面展开图的识别，最简单有效的方法是动手操作.

图2

考点3几何体的三视图

例4（2015年日照卷）小红在观察由一些相同小立方块搭成的几何体时，发现它的主视图、俯视图、左视图均为如图3，则构成该几何体的小立方块的个数有（）．

A.3个B.4个

C.5个D.6个

分析与解：由俯视图为如图3可知正方体排成“前二后一”、“左二右一”共三堆；由主视图可知前左一堆有2层，前右一堆有一层；由左视图可知后面一堆有一层．因此，共有四个正方体.选B.

温馨小提示：从俯视图入手，确定“堆数”，由其他视图分别确定各堆的层数.

图3

考点4相交线与平行线

例5（2015年邵阳卷）将直尺和直角三角板按如图4方式摆放，已知∠1=30°，则∠2的大小是（）．

A.30°B.45°

C.60°D.65°

分析与解：由∠1、∠3互余可得∠3=90°-∠1=60°；由直尺的两边互相平行，得∠2=∠3=60°．选C．

温馨小提示：要熟练掌握平行线的判定与性质.

图4

考点5三角形

例5（2015年佛山卷）各边长度都是整数、最大边长为8的等腰三角形共有个．

分析与解：各边长度都是整数、最大边长为8的等腰三角形，三边长可以为：（1，8，8）；（2，8，8）；（3，8，8）；（4，8，8）；（5，5，8），（5，8，8）；（6，6，8），（6，8，8）；（7，7，8），（7，8，8）；（8，8，8）．故符合条件的三角形共有11个．填：11．

温馨小提示：确定三角形三边长时，要注意三角形任何两边之和大于第三边，任何两边之差小于第三边.

考点6等腰三角形

例7（2015年泰州卷）如图5，△ABC中，AB越AC，D是BC的中点，AC的垂直平分线分别交AC、AD、AB于点E、O、F，则图中全等三角形的对数是（）.

A.1对B.2对C.3对D.4对

分析与解：由AB越AC，D为BC中点，得AD是BC的垂直平分线，从而ΔABD≌ΔACD，ΔOBD≌ΔOCD，ΔOAB≌ΔOAC；又EF垂直平分AC，所以ΔOAE≌ΔOCE．共有四对全等三角形.选D.

温馨小提示：等腰三角形有许多性质，主要有等边对等角、等角对等边和三线合一等，这些性质的运用常在综合题中出现.

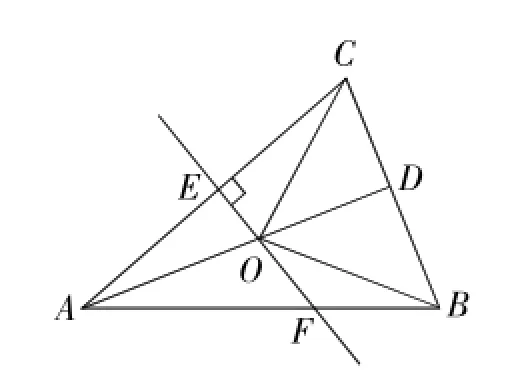
图5

考点7平行四边形

例8（2015年衢州卷）如图6，在▱ABCD中，已知AD越12cm，AB越8cm，AE平分∠BAD交BC于点E，则CE的长等于（）.

A.8cmB.6cm

C.4cmD.2cm

分析与解：∵四边形ABCD是平行四边形，

亦AD∥BC，AD越BC，亦∠DAE越∠AEB，

又疫AE平分∠BAD，亦∠DAE越∠EAB，亦∠EAB越∠AEB，

亦AB越BE，亦CE越BC原BE越12原8越4(cm)．选C.

温馨小提示：平行四边形的性质体现在“四对”，即对边平行且相等，对角相等，对角线互相平分，中心对称图形.其次，邻角互补、被对角线分成四个三角形的面积相等也是常考点.

图6

考点8矩形

例9（2015年自贡卷）如图7，在矩形ABCD中，AB越4，AD越6，E是AB边的中点，F是线段BC边上的动点，将△EBF沿EF所在直线折叠得到ΔEB忆F，连接B忆D，则B忆D的最小值是（）.

分析与解：连接ED，则在ΔEDB忆中，B忆D跃DE原EB忆，当点B忆落在ED上时，B忆D最小，等于DE原EB忆援

图7

根据翻折对称性，EB义越EB越2，

温馨小提示：矩形是特殊的平行四边形，其主要性质有对角线相等、四个角都是直角以及中心对称性、轴对称性，其中以折叠为背景的问题是中考命题的热点.

考点9菱形

例10（2015年青岛卷）如图8，菱形ABCD的对角线AC、BC相交于点O，E、F分别是AB、BC边上的中点，连接EF，若EF越，BD越4，则菱形ABCD的周长为（）．

图8

温馨小提示：菱形的四边相等、对角线互相垂直平分且每条对角线平分每对内角.菱形的面积等于对角线乘积的一半及轴对称是常考点.

考点10多边形

例11（2015年丽水卷）一个多边形的每个内角均为120°，则这个多边形是（）.

A.四边形B.五边形C.六边形D.七边形

分析与解：由多边形的每个内角均为120°，得每个外角为180°-120°越60°．又多边形的外角和是360°，∴这个多边形的边数是：360÷60＝6．选C.

温馨小提示：n边形的内角和公式（n原2）·180°及外角和为360°是解决多边形边数与内角度数问题的主要工具.

考点11圆

例12（2015年南宁卷）如图9，AB是⊙O的直径，AB越8，点M在⊙O上，∠MAB越20°，N是弧MB的中点，P是直径AB上的一动点，若MN越1，则△PMN周长的最小值为（）．

A.4B.5C.6D.7

分析与解：∵N关于AB的对称点N忆，

亦MN忆与AB的交点P忆即为ΔPMN周长的最小时的点，

疫N是弧MB的中点，

图9

∴∠A越∠NOB越∠MON越20°，

∴∠MON忆越60°，∴ΔMON忆为等边三角形，

∴MN忆越OM越4，∴△PMN周长的最小值为4垣1越5．选B．

温馨小提示：圆的性质较多，主要有圆心角定理，圆周角定理，弧、弦、弦心距、圆心角关系定理，垂径定理等.

考点12扇形

例13（2015年河南卷）如图10，在扇形AOB中，∠AOB越90°，点C为OA的中点，CE⊥OA，以点O为圆心，OC的长为半径作扇形交OB于点D，若OA越2，则阴影部分的面积为．

分析与解：连接OE.

∵CE⊥OA，C为OA的中点，

亦∠OEC越30°，∠COE＝60°.

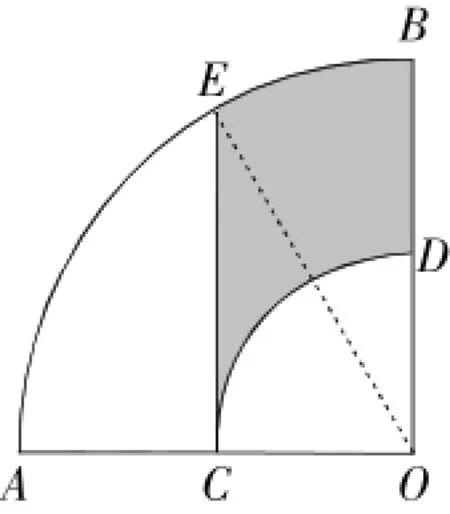
图10

∵∠AOB越90°，∴∠BOE越∠AOB原∠COE越30°，

考点13圆锥

例14（2015年德州卷）如图11，要制作一个圆锥形的烟囱帽，使底面圆的半径与母线长的比是4：5，那么所需扇形铁皮的圆心角应为（）.

A.288°B.144°C.216°D.120°

分析与解：设扇形圆心角为n°．由已知可设底面圆的半径为4x，母线长为5x，则底面圆的周长为2仔·4x越8仔x，扇形铁皮的弧长为，解得n越288.选A．

图11

温馨小提示：圆锥母线l、底面圆的半径r和高h构成直角三角形，满足l2越r2垣h2.

责任编辑：王二喜