小微企业抽样调查的样本轮换

万舒晨，金勇进

(1.中国人民大学 统计学院，北京 100872；2.国家统计局 工业统计司，北京 100826；3.中国人民大学 应用统计科学研究中心，北京 100872)



【统计理论与方法】

小微企业抽样调查的样本轮换

万舒晨1,2，金勇进1,3

(1.中国人民大学 统计学院，北京 100872；2.国家统计局 工业统计司，北京 100826；3.中国人民大学 应用统计科学研究中心，北京 100872)

目前，小微企业抽样调查数据受到各级政府和社会各界的高度关注。针对小微企业单位新增、消亡变动频繁的特点，研究了总体单位及样本量变动的一般条件下的样本轮换理论，对样本轮换率和估计量进行了探讨，扩大了研究结果的适用范围，得到了简单随机抽样、分层抽样中样本轮换的有关结论，对估计量的抽样误差进行了有效控制，并进行了相关实证研究，最后提出了构造适合小微企业连续性抽样调查的样本轮换设计模式和方法。

样本轮换；小微企业；样本轮换率；估计量

一、引 言

目前，小微企业调查数据受到各级政府和社会各界的高度关注。小微企业规模小、数量多的特点，决定了抽样调查成为其统计调查的主要方法。然而，小微企业实际抽样调查中暴露出一些问题，万舒晨和金勇进对面临的相关问题进行了总结并指出改进方法，其中尤以连续性抽样调查问题亟需重点解决[1]。

在连续性抽样调查中，固定样本设计能够降低调查成本、使前后期调查数据实现可比，但存在样本老化、样本疲劳等问题；全新样本设计能及时采取最新样本、减少样本疲劳，但往往造成调查成本增加，也不利于实现对连续性调查数据的跟踪和对比。因而统计学家提出了样本轮换的方法，同时吸取了固定样本和全新样本两种抽样设计的优点。小微企业自身的特点和抽样设计的目标，决定了在小微企业的连续性抽样调查设计中，采用样本轮换方法是较为合适的选择。

关于样本轮换的国内外研究文献，在总体单位及样本量固定条件下，主要集中在样本轮换模式和方法、样本轮换率控制和估计量构造等几个方面。

样本轮换模式和方法。Eckler将样本轮换的模式分为单水平样本轮换和多水平样本轮换[2]；曾五一将样本轮换的具体方法分为重复子样本轮换法和随机轮换法[3]180-184。

样本轮换率控制。在总体单位及样本量固定条件下，Cochran总结了前人关于简单随机抽样中样本轮换率的研究成果[4]523-527，卢宗辉等提出了确定样本轮换率的多种方法[5]，张宁研究了分层抽样理论的样本轮换率[6]，刘建平和陈光慧推导了利用辅助信息建立回归模型基础上的样本轮换率结论[7]。

估计量构造。在总体单位及样本量固定条件下，Cochran构造了基本形式的样本轮换组合估计量；进一步地，多位学者以单水平样本轮换的设计模式为基础，提出了各种形式的组合估计量[8-10]；Park等研究了多水平轮换调查下的组合估计量问题[11]。

然而，在实际调查中，小微企业前后两期总体单位往往存在较为明显的变动；即使是在相同抽样精度要求下，前后两期所需样本量往往也不相同。因而，总体单位及样本量固定条件下的经典样本轮换模型对小微企业不适用。

针对小微企业单位变动频繁的特点，本文对总体单位及样本量变动条件下的样本轮换进行了独创性的研究，提出适合小微企业自身特点的样本轮换模式和方法，得到其最优样本轮换率和估计量的相关结论，并进行了实证研究。

二、最优样本轮换率及估计量构造

(一)简单随机抽样

(1)

(2)

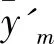
(3)

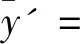
(4)

(5)

对式(5)关于φ求1阶导数

(6)

再求2阶导数

(7)

将式(7)代入式(5)，可得：

(8)

将式(1)和式(3)代入式(8)，得：

(9)

(10)

于是利用前期辅助信息设计的组合估计量，减少的方差为：

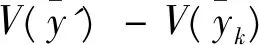
(11)

前后两期总样本量n和k均已知确定，由于v=k-n+u，故根据式(9)有：

(12)

对式(12)关于u求1阶导数，有：

(13)

再求2阶导数，有：

(14)

(15)

(16)

可以看出，这与总体单位及样本量固定条件下的结论一致，即最优样本轮换率与现期样本量k和换进的新样本量大小v无关。

(17)

将式(15)代入式(9)，可得最优轮换比例时的方差为：

(18)

另外，对于总体总量及其方差的估计有：

(19)

(20)

(二)分层抽样

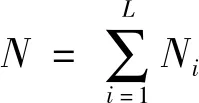
(21)

其中，0≤φi≤1为层i内组合估计量的权重，bi为层i内保留样本单位现期调查值对前期调查值的回归系数。

类似简单随机抽样部分的证明，可得在分层抽样下的样本轮换设计中，对层i有如下结论：

1.层i内的最优权重为：

(22)

(23)

表明构造的估计量方差有所减少，精度得到提高；

3.在层i内，最优的样本轮换率表示为：

(24)

4.当各层均采用各自最优的轮换比例时，得到估计量的最小方差：

(25)

三、实证研究

小微企业单位变动频繁，总体单位及样本量固定条件下的经典样本轮换模型并不适用。因而，本文在总体单位及样本量变动条件下，得到了简单随机抽样和分层抽样设计的样本轮换模式和估计量的独创研究结果。这里针对两个地区小微工业企业样本轮换实例，运用简单随机抽样和分层抽样中的相关样本轮换理论进行实证研究。

(一)简单随机抽样中样本轮换的实证研究

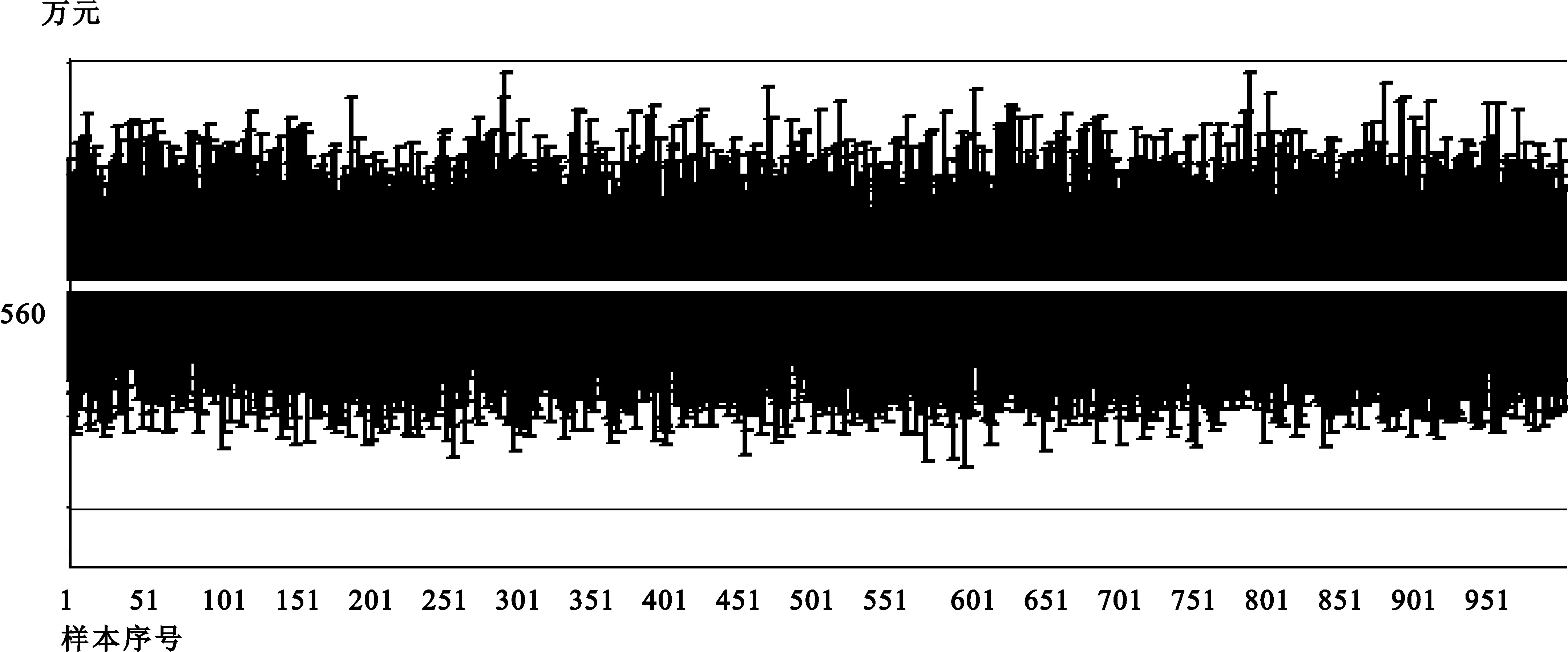
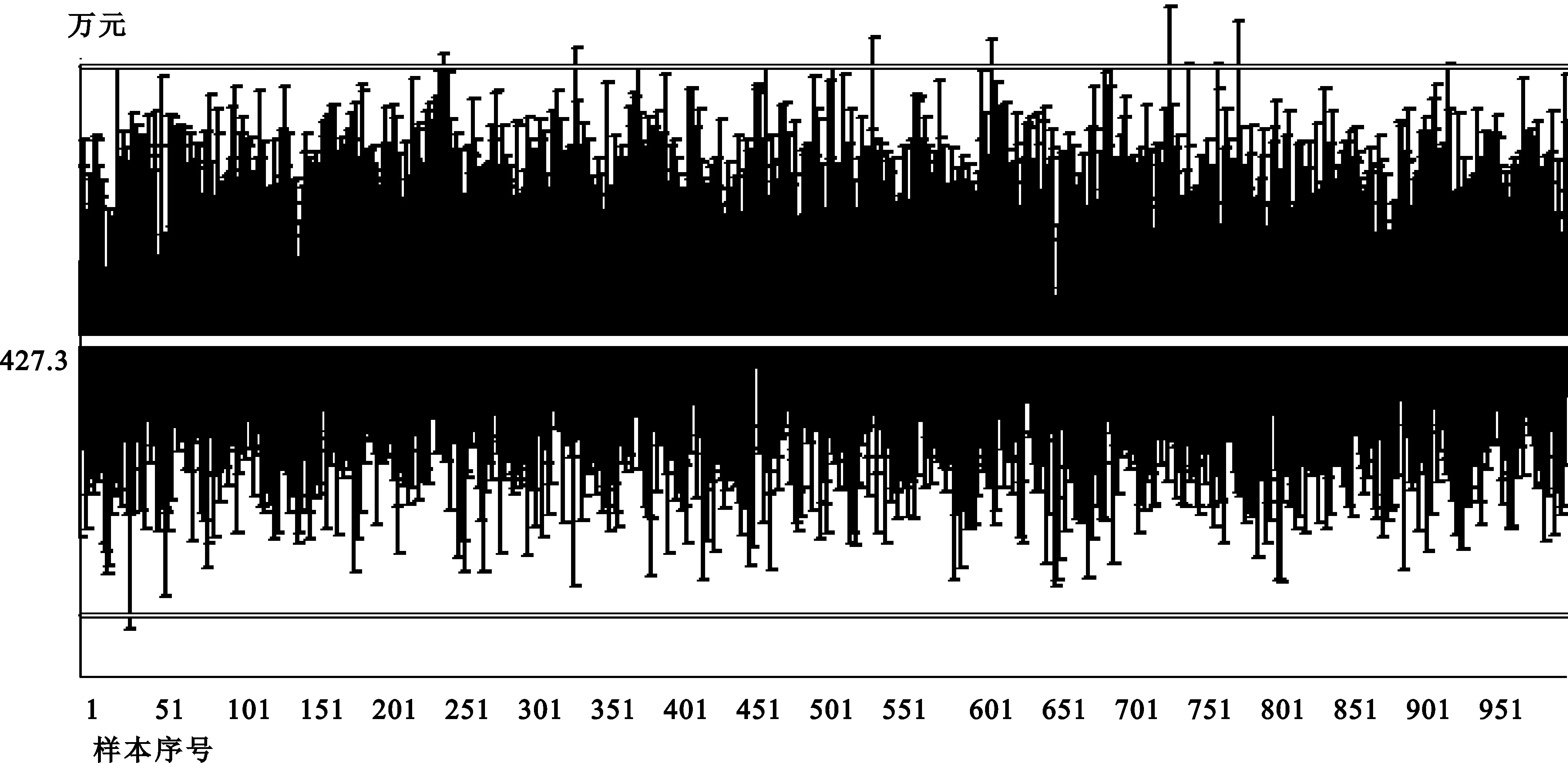
A地区前期小微工业企业总体单位数为N=25 318，现期总体单位数为K=26 324，K>N，总体单位发生变动。利用简单随机抽样的样本量计算公式，并根据实际情况微调，确定前期样本量为n=628，现期样本量为k=615，从而现期样本量小于前期样本量，即k

为保证抽样结果的稳定性，不因一次抽样的随机性而引起较大的偏差，对样本轮换过程编写计算机程序重复进行1 000次。对于每次样本轮换过程，均可以构造95%置信区间。重复进行1 000次样本轮换过程，结果发现所有95%置信区间均包含总体企业收入均值(图1显示了1 000次重复样本轮换的95%置信区间结果，其中企业平均收入真值为560万元)。

图1 1 000次简单随机抽样下重复样本轮换置信区间结果

在1 000次抽样下重复样本轮换的过程中，每次同时进行了单独抽样进行对比，即对现期总体不考虑样本轮换率的最优控制而进行独立抽样。结果表明，样本轮换下构造的组合估计量的精度，比单独抽样估计量的精度有所提高(即样本轮换的1 000个样本企业收入均值间的标准差较小，详见表1)。

表1 简单随机抽样下样本轮换与单独抽样精度比较表

(二)分层抽样中样本轮换的实证研究

B地区小微工业企业发展较好、单位数较多，前期总体单位数为N=231 537，现期总体单位数为K=297 851，K>N，总体单位发生较大的变动。前后两期总体均根据行业门类分层，即分为采矿业、制造业、电力热力燃气及水生产和供应业三层。采用奈曼分配下的分层抽样样本量计算公式，并根据实际情况进行微调，确定前期样本量为n=500，现期样本量为k=530，从而现期样本量大于前期样本量，即k>n。前期及现期具体分层情况如下表：

表2 B地区前期及现期分层情况表

为保证抽样结果稳定，不因一次抽样的随机性而引起较大偏差，对样本轮换过程编写计算机程序重复进行1 000次。对每次样本轮换过程，均根据样本企业收入均值和估计量方差，构造95%置信区间。重复进行1 000次样本轮换过程，发现仅出现11次95%置信区间不包含总体企业收入均值的情况(图2显示了1 000次重复样本轮换的95%置信区间结果，其中企业平均收入真值为427.3万元)。

图2 1 000次分层抽样下重复样本轮换置信区间结果

在1 000次分层抽样下重复样本轮换的过程中，每次同时进行了单独抽样进行对比。结果表明，样本轮换下构造的组合估计量的精度，比单独抽样估计量的精度有所提高(详见表3)。

表3 分层抽样下样本轮换与单独抽样精度比较表

对比表1和表3 ，A地区样本轮换估计量标准差减少29.3%，B地区减少4.3%，显然A地区精度提高得更多。对式(18)关于ρ2求导，可知

(26)

四、总 结

本文针对小微企业特点，剔除“总体和样本单位数固定”的条件束缚，研究了总体单位及样本量变动条件下样本轮换的相关理论，得到了简单随机抽样和分层抽样中样本轮换的结论。根据理论指导，小微企业应该选择适合自身特点的样本轮换设计和方法。

小微企业会计账务报表大多不太健全，如果采用多水平样本轮换设计模式，往往需要调查对象主观回忆前期数据，造成不必要的非抽样误差；另外，小微企业消亡变动较为频繁，如果采用不完全单水平样本轮换设计模式，退出样本再次重新返回样本时容易造成样本单位的大量缺失。因而针对小微企业，最合适的样本轮换设计模式应为狭义的单水平样本轮换。

小微企业自身特点明显，企业新增、消亡变动非常频繁，如果采取重复子样本轮换法，无法及时将消亡样本单位剔除，也不能及时将新增小微企业加入到样本中，从而不能有效维护小微企业的样本代表性。因此小微企业进行样本轮换时，应采取随机轮换的方法，在抽样框更新的前提下实现新老样本之间的轮换，有效提高样本的代表性。

综上所述，小微企业进行样本轮换时，应采取总体单位及样本量变动条件下的狭义单水平样本轮换模式，并且采取随机轮换的方法，提高样本代表性。

[1] 万舒晨，金勇进. 小微工业企业抽样调查的问题及改进建议[J].调研世界，2015(4).

[2] Eckler A R. Rotation Sampling[J]. The Annals of Mathematical Statistics，1955，26(4).

[3] 曾五一. 统计调查体系与调查方法问题研究[M]. 北京：中国统计出版社，2009.

[4] 科克伦(Cochran W.G.).抽样技术[M]．张尧庭，吴辉，译．北京：中国统计出版社，1985.

[5] 卢宗辉，陈仁恩. 社会经济调查中的样本轮换问题研究[J]. 广播电视大学学报：哲学社会科学版，2005(1).

[6] 张宁.分层抽样下的样本轮换理论研究[J].统计与信息论坛，2008，23(4).

[7] 刘建平，陈光慧.基于回归组合技术的连续性抽样估计方法研究[J].统计与信息论坛，2008，23(10).

[8] Hansen M H，Hurwitz W N，Nisselson H，Steinberg J. The Redesign of the Census Current Population Survey[J].Journal of the American Statistical Association，1955，50.

[9] Gumey M，Daly J F.A Multivariate Approach to Estimation in Periodic Sample Surveys[C]. Proceedings of the Social Statistics Section, American Statistical Association，1965.

[10]Singh A C，Kennedy B，Wu S，Brisebois F. Composite Estimation for the Canadian Labour Force Survey[C]. Proceedings of the Survey Research Methods Section，American Statistical Association，1997.

[11]Park Y S，Choi J W，Kim K W. A Balanced Multi-level Rotation Sampling Design and its Efficient Composite Estimators[J].Journal of Statistical Planning and Inference，2007，137(2).

[12]金勇进.抽样：理论与应用[M]．北京：高等教育出版社，2010.

(责任编辑：马 慧)

Sample Rotation of Sampling Survey about the Small and Micro Enterprises

WAN Shu-chen1a,2，JIN Yong-jin1a,1b

(a.School of Statistics，b.Center for Applied Statistics，1.Renmin University of China，Beijing 100872，China；2.Department of Industrial Statistics，National Bureau of Statistics，Beijing 100826，China)

At present，the sampling survey data of the small and micro enterprises has been highly concerned by the government and community of China. According to the characteristics of frequently changing about the small and micro enterprises，some new firms may come into being while a few existed ones may quit from business，so we study the sample rotation theory under the condition of population and sample size changing，and discuss the sample rotation ratio and estimator in order to expand the scope of research results. Under the general condition of population and sample size changing, we explorer sample rotation in simple random sampling and stratified sampling, and make effective control on sampling error of the estimator. At last we do some empirical research，and propose the sample rotation design and method for successive sampling of the small and micro enterprises.

sample rotation；small and micro enterprises；sample rotation ratio；estimator

2015-11-13

全国统计科学研究重点项目《小微工业企业抽样调查问题研究》(2013LZ34)；北京市社科基金重点项目《基于北京市地理分布的空间抽样设计研究》(14JGA022)；国家社科基金项目《大数据背景下非概率抽样的统计推断问题研究》(15BTJ014)

万舒晨，男，江苏扬州人，博士生，高级统计师，研究方向：抽样调查技术与数据分析； 金勇进，男，北京人，教授，博士研究生导师，研究方向：抽样调查。

C811

A

1007-3116(2016)11-0014-06