因材施教在克拉默法则教学中的体现

唐锋

（常熟理工学院数学与统计学院，江苏 常熟 215500）

因材施教在克拉默法则教学中的体现

唐锋

（常熟理工学院数学与统计学院，江苏 常熟 215500）

针对不同专业以及不同层次的学生，给出不同的证明方法讲授克拉默法则，充分调动学生对学习线性代数的兴趣。本文主要介绍三种证明方法：行列式方法；矩阵方法；几何方法。

克拉默法则；矩阵；因材施教

一、引言

克拉默法则是行列式性质的一个典型应用。内容如下：

定理（克拉默法则）如果线性方程组

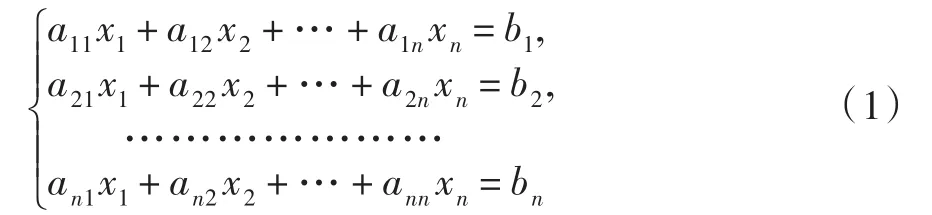
教师在讲解克拉默法则时一般都是直接给出定理，接着按照教材［1］的证明顺序首先证明方程解的存在性，再证明唯一性。这很不符合一般本科一年级学生的思维习惯，学生在中学学习解方程总是先求解再验证解的正确性；再者，学生从心底里不愿意接受直接将解代入方程验证，因为他们没有弄清楚这个解是怎么得到的；最后，在教材证明中求和符号“∑”大量使用，纯推理，没有直观感受的大多数学生不感兴趣。时间长了，多数学生就会对这门课程产生抵触情绪，从而使教学过程陷入恶性循环。

笔者所在单位是一所省属一般理工类院校，所授学生有属于数学专业、对数学要求较高的信息及电子工程等专业，还有对理论推导要求不高的经济管理专业等。在多年的教学中，笔者尝试根据不同类型的学生设计不同的讲授，既让学生拓宽了视野，又学到了比较新颖的知识，还增加了对这门课的兴趣，同时也不让学生“闲着”，充分调动学生积极思考，动员部分班级学生查阅各种资料，促进学生主动学习。

在引入克拉默法则时，首先应该说明：我们已经完成了行列式性质的学习，清楚了行列式的多种计算方法，但是行列式的应用在哪里呢？本节就介绍行列式的一个应用：线性方程组的求解。然后引导学生回忆行列式是如何引进的，学生回答：行列式是通过中学求解二元和三元一次方程组，看出解中分母的规律而引出定义的。此时引导学生往另外一个方向思考：我们已经知道二元和三元一次方程组的解形式都有一种很强的规律，那么将方程组的未知数变量增加到n个，方程的个数也增加到n，此时该线性方程组如何求解呢？这就是本节所要解决的主要内容。

二、行列式证明方法

分析定理中包含了三个结论：1.方程组有解；2.方程组解唯一；3.方程组的解可通过定理中的形式给出。

对于数学专业的学生，要求加强培养其推理能力，为此给出三种行列式的证明方法。

这样的证明并没有起到简化作用，但是延承了学生的思维习惯，所以学生较容易接受。

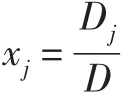
证法2对于1≤j≤n，因为

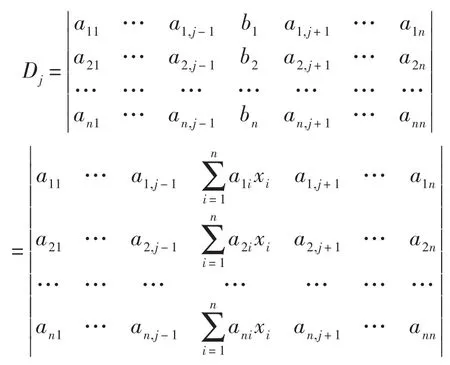
上述行列式的第k列乘(-xk)（k=1,…,j-1,j+1,…,n）加到第j列，得到

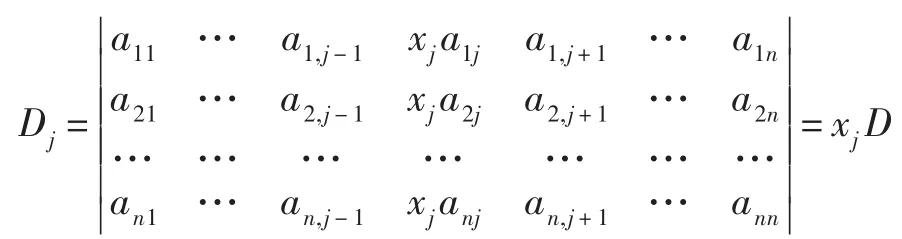
可以发现，证法2比证法1要优越很多。证明题的思路经常是要从结论中寻找线索，这符合学生的思维方式，数学专业的学生也比较喜欢这样的理论推理。而且证明过程很简短，关键是还用到了行列式的性质，很好地体现了学以致用、学有所用的教学要求。

教材［2］提供了克拉默法则的另外一种行列式的证明，为体现完整性，在此一并给出。

证法3考察有两行相同的n+1阶行列式

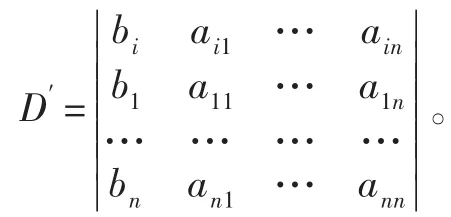
显然D′=0。D′的第一行中aij的代数余子式为

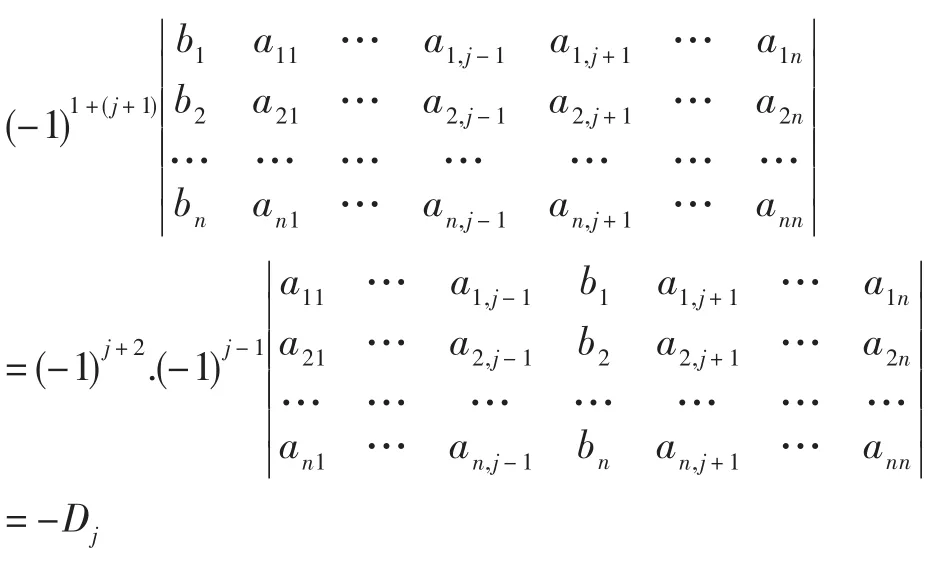
D′按照第一行展开，于是得到0=D′=biD-ai1D1-…-ainDn，即

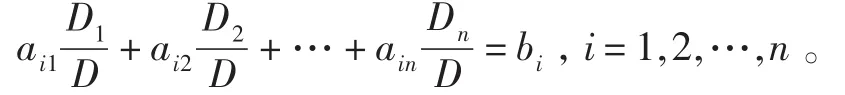
注意证法3只给出了定理中解的存在性证明，但没给出唯一性的证明，所以证明是不完整的。学生比较很容易发现：证法2在三种证明中是最好的。

三、矩阵证明方法

对于非数学专业但又对数学要求较高的学生，笔者尝试用矩阵证明的方法讲授给学生，介绍如下。

证法4首先按照教材［3］在第二章的证明方法讲授。线性方程组（1）可以用矩阵形式表示为

其中A=(aij)n×n,X=(x1,x2,…,xn)T,β=(b1,b2,…,bn)T。

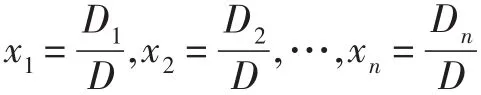
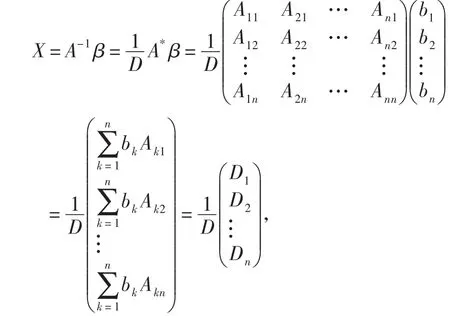
这是很多线性代数教材中的证法，笔者不因循守旧，为拓宽学生的视野及思路，介绍如下的证明方法。

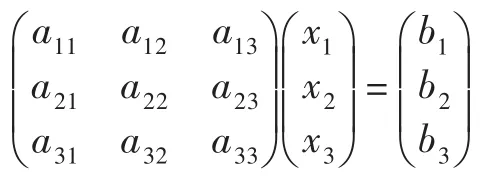
一是构建事业平台。智库要有事情做，有研究的问题、项目、课题等，要有相关的科学有效的理论、方法、信息、手段等的支持，也要有专业、有水平团队支撑；

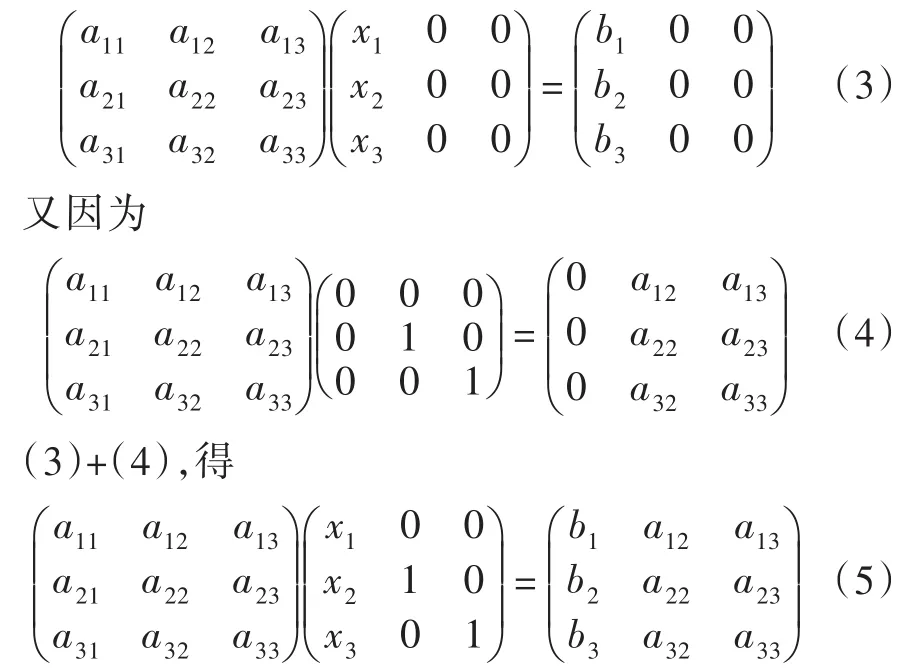
对于非数学专业的学生，这样的证明已经足够，工科学生一般是要学会应用，理论推导应该少讲，但也不能完全不讲，证法5非常适合这类专业的学生。另外，证法5也是很多国外教材使用的方法，笔者介绍给学生也是为了使学生了解国外教材的经典方法，从而拓宽其视野。对于经济管理类的学生因为学时较少，理论基本可以不讲，只需要证法4就能完全满足学生的需要，其他的方法可以讲义的形式发给学生阅读，或者布置为作业，让学生查阅资料。

四、几何证明方法

目前很多大专院校已经将线性代数与解析几何合并为一门课程，但是部分教材只是代数与几何内容机械的穿插，并没有很好结合。为使我校统计专业的学生能真正体会到代数与几何的有机结合，笔者介绍用几何方法证明克拉默法则。

首先让学生理解行列式的几何意义（以下的介绍可见文献［5］）。

当n=1时，一阶行列式就是一个实数a，它在数轴上表示以原点为起点，实数a为标点的终点的有向线段的有向长度，显然a＞0时，该有向长度为正；a＜0时，该有向长度为负；a=0时，该有向长度为零。

当n=3时，行列式是“平行六面体的有向体积”，可参看教材［4］，这里不再赘述。

证法6[5]为方便叙述，仅就n=2时给出证明。此时方程组（1）变为

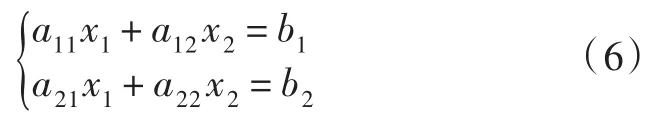
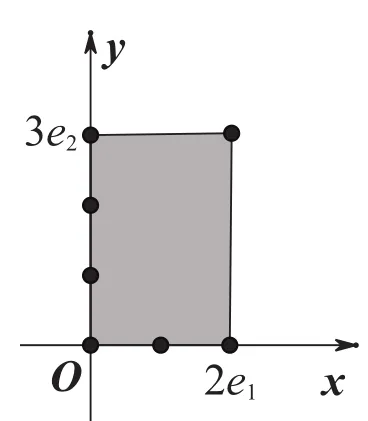
图1

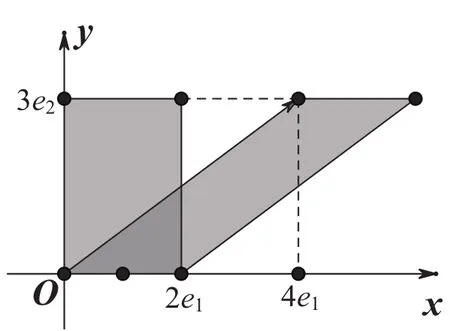
图2

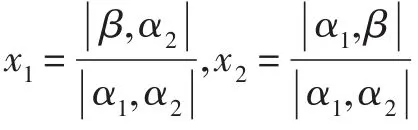
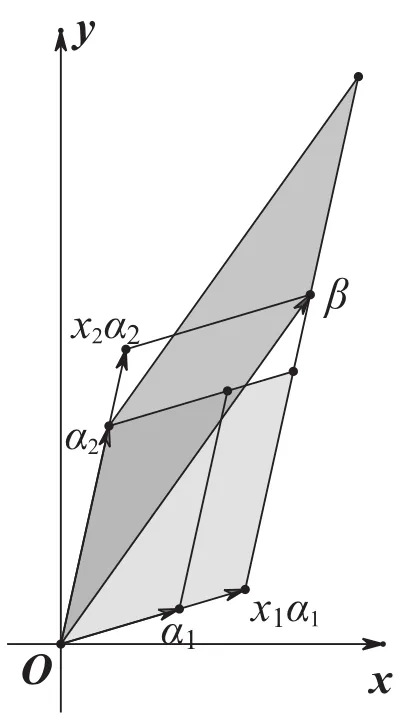
图3

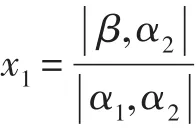
可以看出，证法6完全依靠几何的直观理解就可证明，并且此直观理解可推广到一般n维空间的形式。作为练习，可请学生板演x2的求解，作为思考题，可布置学生用几何图形证明n=3的情形。一个完全是代数的问题在n=2或n=3时可以用纯几何的方法证明，这很好体现了线性代数与解析几何的有机结合，达到了教学目的。

五、结语

克拉默法则还有许多的证明方法，例如用矩阵的初等变换证明［6］等，这里不再叙述。另外还应指出的是，克拉默法则只是解决了一类特殊的线性方程组的求解问题，对于更一般的线性方程组求解并没有解决，这为后续内容打下了很好的伏笔。

这些不同的尝试，对于本节知识的掌握乃至提高学生对这门课的学习兴趣产生了良好的效果。总之，因材施教需要教师钻研教材，善于了解熟悉学生的学习能力，更需要课后阅读大量的文献资料，这样才能真正提高教学水平，让学生学到更多更好的知识。

［1］北京大学数学系代数小组.高等代数［M］.3版.北京：高等教育出版社，2003：83-86.

［2］同济大学数学系.线性代数［M］.3版.北京：高等教育出版社，2004：22-26.

［3］同济大学数学系.线性代数［M］.5版.北京：高等教育出版社，2007：53-54.

［4］吕林根，许子道.解析几何［M］.4版.北京：高等教育出版社，2006：53-58.

［5］谢琳，张静.从几何直观理解行列式与Cramer法则［J］.高等数学研究，2009（1）：12.

［6］孙伯奎.克莱姆法则的一个新证明［J］.山东大学学报（理学版），2003（2）：38.

Teaching Students in Accordance with Their Aptitude Embodying Cramer Rule in Teaching

TANG Feng
(School of Mathematics and Statistics,Changshu Institute of Technology,Changshu 215500,China)

According to different majors and different levels of the students,this paper gives several ways to prove Cramer rule,which can fully mobilize students'interest in learning linear algebra.The paper mainly introduces three methods to prove the determinant method,matrix method and geometric method.

Cramer Rule;Matrix;teaching students in accordance with their aptitude

O151.2；G424.21

A

1008-2794（2016）06-0102-04

2015-10-14

唐锋（1973—），男，江苏泰兴人，副教授，硕士，主要研究方向为有限群。