某型飞机模型飞行试验地面滑跑控制研究

刘进, 叶德章, 方桂才, 贾涛

(中国空气动力研究与发展中心 计算空气动力学研究所, 四川 绵阳 621000)



某型飞机模型飞行试验地面滑跑控制研究

刘进, 叶德章, 方桂才, 贾涛

(中国空气动力研究与发展中心 计算空气动力学研究所, 四川 绵阳 621000)

地面滑跑纠偏的目标是控制飞机沿跑道中心滑行,避免因发动机安装偏差、侧风扰动、跑道不平、飞机结构不对称等非理想特性,出现飞机滑出跑道的情况。首先建立飞机地面滑行动力学方程,并分析三轮、两轮滑跑阶段的受力情况,在此基础上设计了副翼、方向舵与前轮联动的控制策略。在Simulink平台上搭建飞机的地面滑跑全量非线性模型,仿真验证了纠偏控制律结构和逻辑的正确性。试验结果表明,滑跑纠偏控制系统空地状态切换平稳,在低速和高速阶段均具有良好的控制效果。

模型飞行试验; 地面滑跑; 动力学模型; 控制纠偏

0 引言

模型飞行试验作为气动力研究的三大手段之一,在军事和民用方面都发挥着重要作用,具有广阔的发展前景,其中轮式滑跑是常用的起飞、着陆方式[1]。

空中飞行阶段的飞机动力学模型已建立了完善的理论体系,很多文献进行了较为细致的描述。对于地面滑跑阶段,机体运动受到地面约束、地面效应和起落架影响,涉及大范围非线性、非定常强耦合问题,与空中飞行相比具有不同的动力学和运动学特性,因而控制较为复杂和困难[2-10]。但是飞机的起飞和着陆,尤其是着陆阶段通常是事故频发环节,据统计,大部分的飞机失事均发生在着陆过程中[4-6]。因此,起飞和着陆是飞行的复杂阶段,同样也是模型飞行试验的关键技术之一,地面滑跑控制律的设计显得尤为重要。

本文的被控对象为前三点式起落架布局,操纵前轮进行转向,单发动机,气动操纵面有:升降舵、副翼、阻力型方向舵。建立了试验模型滑跑阶段横航向的动力学和运动学模型,在此基础上进行了控制律设计,并最终开展了飞行试验验证。

1 飞机滑行动力学方程

飞机的地面滑行阶段受力复杂,为一个多输入多输出系统[7]。起飞阶段涉及到的控制量包含:转向前轮、气动操纵面、发动机油门等;着陆阶段涉及到的控制量为:转向前轮、主轮刹车、气动操纵面等。通过合理的分配规律,产生合适的力与力矩,保证试验模型贴紧地面平稳滑跑,避免横侧向偏离,且使地面与空中模态之间互相衔接和平滑过渡。

为计算方便,统一选用机体坐标系Sb-Oxyz为参考坐标系,并建立试验模型的运动方程。

试验模型质心的线运动方程为:

(1)

式中:v=[u,v,w]T为飞机在机体轴上的运动速度分量;F=[Fx,Fy,Fz]T为飞机所受的合外力分量;θ,φ分别为俯仰角和滚转角。

试验模型为面对称飞行器,机体关于Oxz平面对称,绕各坐标轴转动的角运动方程为:

(2)

式中:p,q,r为三轴角速度分量;M=[Mx,My,Mz]T为试验模型所受外力的合力矩;Ix,Iy,Iz,Izx分别为惯性矩与惯性积。

2 滑跑受力分析

随着飞机滑行速度的提高,地面滑跑分为三轮接地滑行与后轮接地两轮滑行两个阶段,下面将分别讨论。

2.1 三轮滑跑阶段

三轮滑跑阶段试验模型所受外力较为复杂,忽略次要因素,主要有:机体重力、空气动力、发动机推力、地面作用力(跑道对机轮的摩擦力与支反力),此外飞机还受到上述力所产生的力矩的影响。

(1)重力

由于试验跑道有一定的坡度,试验模型存在停机角,重力在机体坐标系中的分量为:

(3)

重力总是通过飞机重心的,不会产生重力力矩。因此重力对试验模型质心的力矩为零。

(2)空气动力

试验模型的离地速度高达45 m/s,在滑跑过程中气动现象明显,将空气动力转换到机体坐标系中的分量为:

(4)

式中:D,C,L分别为气动阻力、侧力、升力;α,β分别为迎角、侧滑角。为了准确地描述该阶段飞机气动特性,在计算气动系数时,除了计算基本项,还要计入地面效应和起落架对气动特性的影响。

试验模型发动机关于机体对称安装(推力作用点在机体坐标系的坐标(lx,0,lz)),且安装角为零,忽略转子的影响,推力及其力矩在机体坐标系中可近似表达为:

(5)

(4)地面作用力

试验模型在跑道上滑行时主要受到地面支反力和摩擦阻力的作用,当有横向纠偏时还必须考虑侧向力。

①地面支反力和摩擦力

本文忽略机轮弹性的影响,地面支反力P可由起落架支柱的压缩量和压缩速度来计算:

P=∑Pi=∑(ksilpi+kdivpi)

(6)

式中:lpi,vpi分别为起落架三个支柱各自的压缩量与压缩速度;ks,kd分别为起落架支柱的弹性系数和阻尼系数,其值由起落架静态坠落试验得到。

摩擦阻力Q由地面支反力P决定,存在如下关系:

Q=μP=∑μPi

(7)

式中：μ为摩擦系数，与跑道路况直接相关,本文根据试验结果取值0.031。

(4)随着混凝土强度等级的提高，可以提高短柱整体的承载力。在挠度0.25 mm内，承载力的提高幅度和斜率基本重合。混凝土强度等级较高时，在到达极限承载力之后会出现明显的下降曲线，下降幅度大。混凝土强度等级较低时，下降段比较平缓，延性好。混凝土强度等级过高，柱的延性变差，易发生脆性破坏，因此，核心混凝土不宜选用高强混凝土。

②侧向力

本文研究的起落架主轮无转向功能,其在机体坐标系中的偏角恒定为零。将试验模型地速vg在机体坐标系中各轴的分量记做vgx,vgy,vgz,左主轮的侧偏角βml和右主轮的侧偏角βmr如图1所示,其表达式为:

(8)

前轮可绕起落架前支柱偏转,前轮的侧偏角为βn=θL-θn,可由运动学关系进一步求解:

(9)

式中:rw为机轮半径;am为主轮到为试验模型重心投影的纵向距离;bw为主轮距;θL为主轮的偏转角;θn为前轮速度方向与机体x轴的夹角;an为前轮到试验模型重心投影的距离。

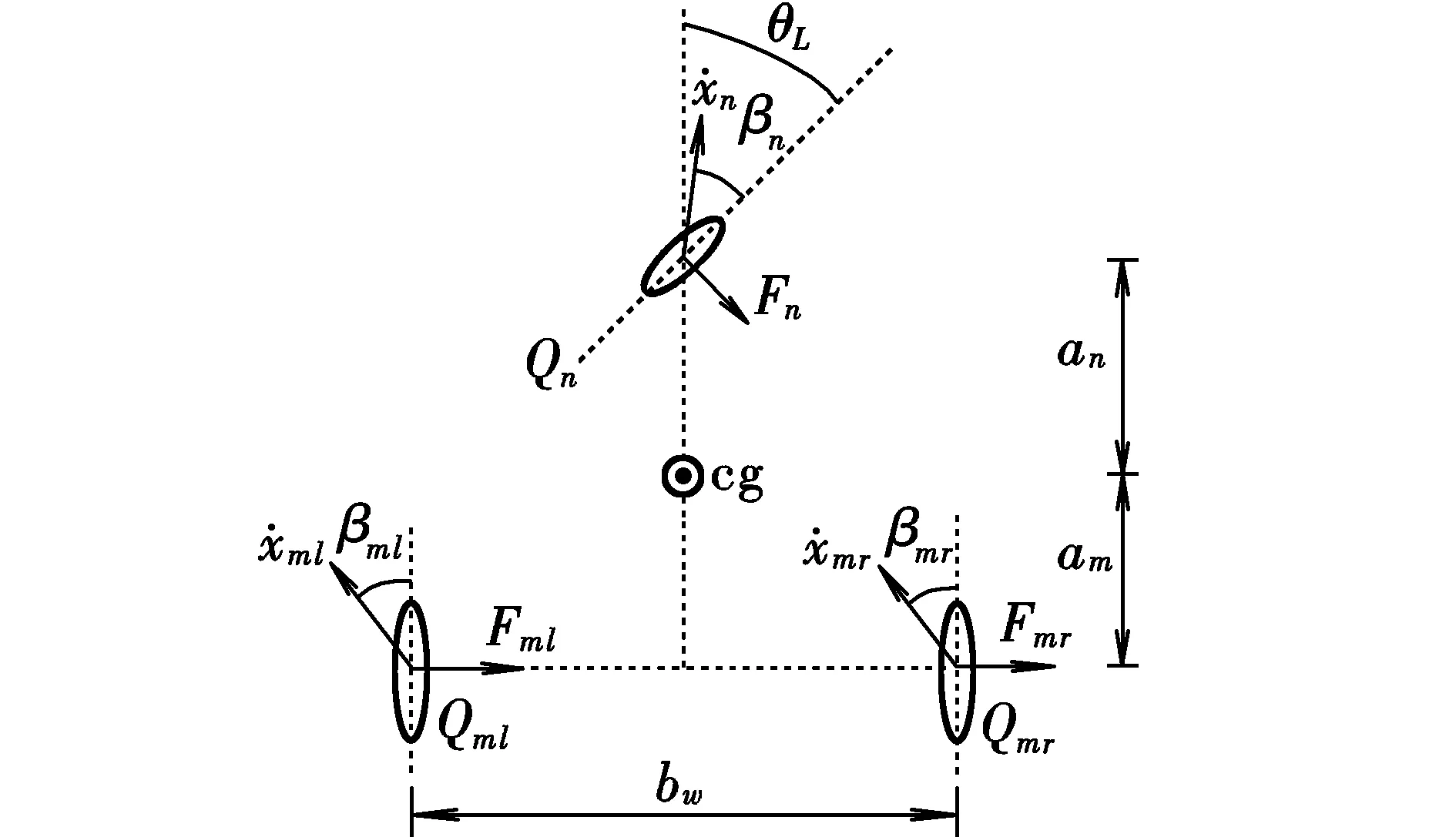
图1 三轮滑跑受力示意图Fig.1 Schematic diagram of stress during three-wheel taxiing

当β较小时(β<5°),侧向力F与侧偏角β存在着线性关系[7],则侧向力可近似表示为:

Fn=Kββn,Fml=Kββml,Fmr=Kββmr

(10)

式中:Kβ为侧向力系数,也称侧偏刚度。

2.2 两轮滑跑阶段

两轮着地滑跑是衔接空中飞行与三轮滑跑的中间过渡状态,持续时间短(通常小于2 s)。此时试验模型仅后轮着地,前轮悬空无纠偏能力,只能靠方向舵控制,地面对试验模型的作用力只作用在两后主轮上,在滚转通道上形成约束。

由于速度高,气动力与力矩的影响增大,发动机推力、重力所引起的力和力矩则与三轮滑跑阶段类似[6],如图2所示,具体分析这里不再详细描述。两轮滑跑阶段的模型求解中俯仰角θ不再等于停机角,q≠0,可令φ=0,p=0。

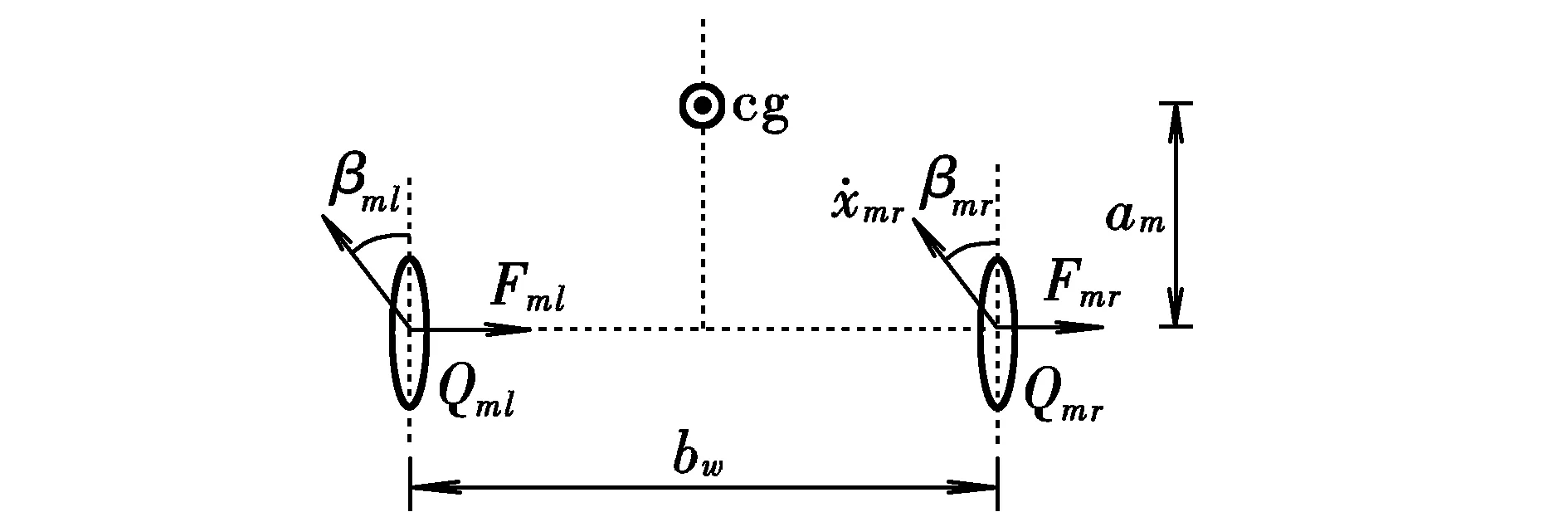
图2 两轮滑跑受力示意图Fig.2 Schematic diagram of stress during two-wheel taxiing

3 纠偏控制律及控制策略设计

飞机在空中巡航飞行时,侧向控制主要利用副翼效率高的特点,通过控制副翼产生滚转来纠正偏航,方向舵自动消除侧滑。地面滑跑的侧向纠偏控制主要依靠前轮导向控制和方向舵控制联动保持滑跑方向,副翼仅在高速状态下来维持翼平。本文采用的地面滑跑纠偏控制律结构示意图如图3所示。

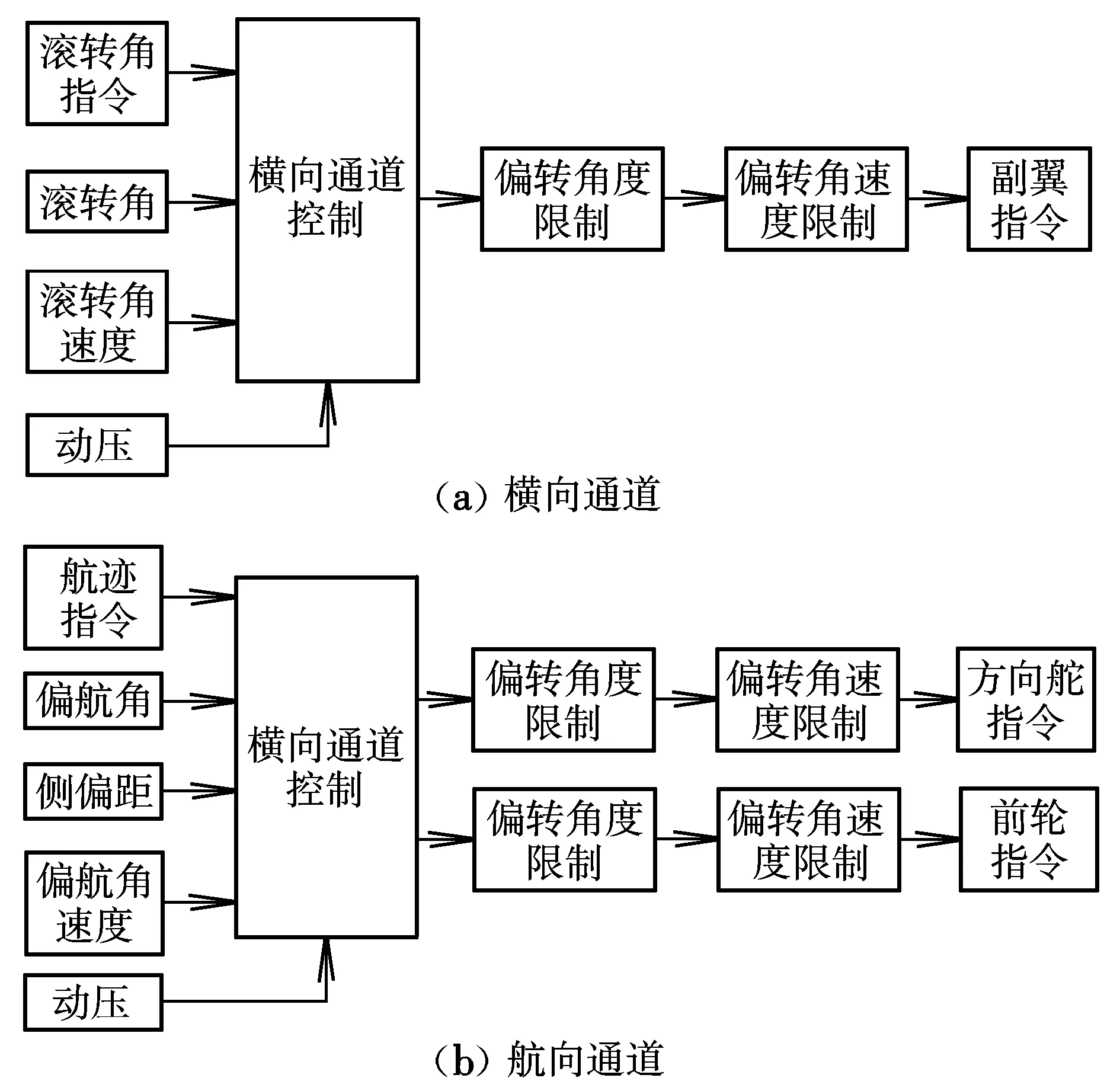
图3 地面纠偏控制律结构示意图Fig.3 Schematic diagram for ground deviation-correction control law

为保证滑跑时从低速到高速均有良好的纠偏效果,控制律参数随动压进行调参,当空速大于30 m/s时,前轮控制指令置零,仅靠方向舵纠偏。此外,考虑飞机硬件条件限制,对方向舵控制指令和前轮导向控制指令的偏转角度与角速度转向速度进行了限制,方向舵的偏转范围为±30°,偏转角速度小于150 (°)/s,前轮的偏转范围为±10°,偏转角速度小于10 (°)/s。在整个控制系统中,将人的优先级设置为最高,当飞行操纵手发现异常情况时,可随时将自主指令断开,进行应急处置。

4 仿真分析

4.1 系统建模

为验证控制律结构的正确性,在Simulink平台上建立了仿真环境,描述飞机滑跑过程,如图4所示。

仿真时预留有遥控器接口,飞机的实时姿态在三维视景中显示,可将飞行操纵手的视觉感受与操作输出连接到仿真回路,实现“人在回路”仿真。

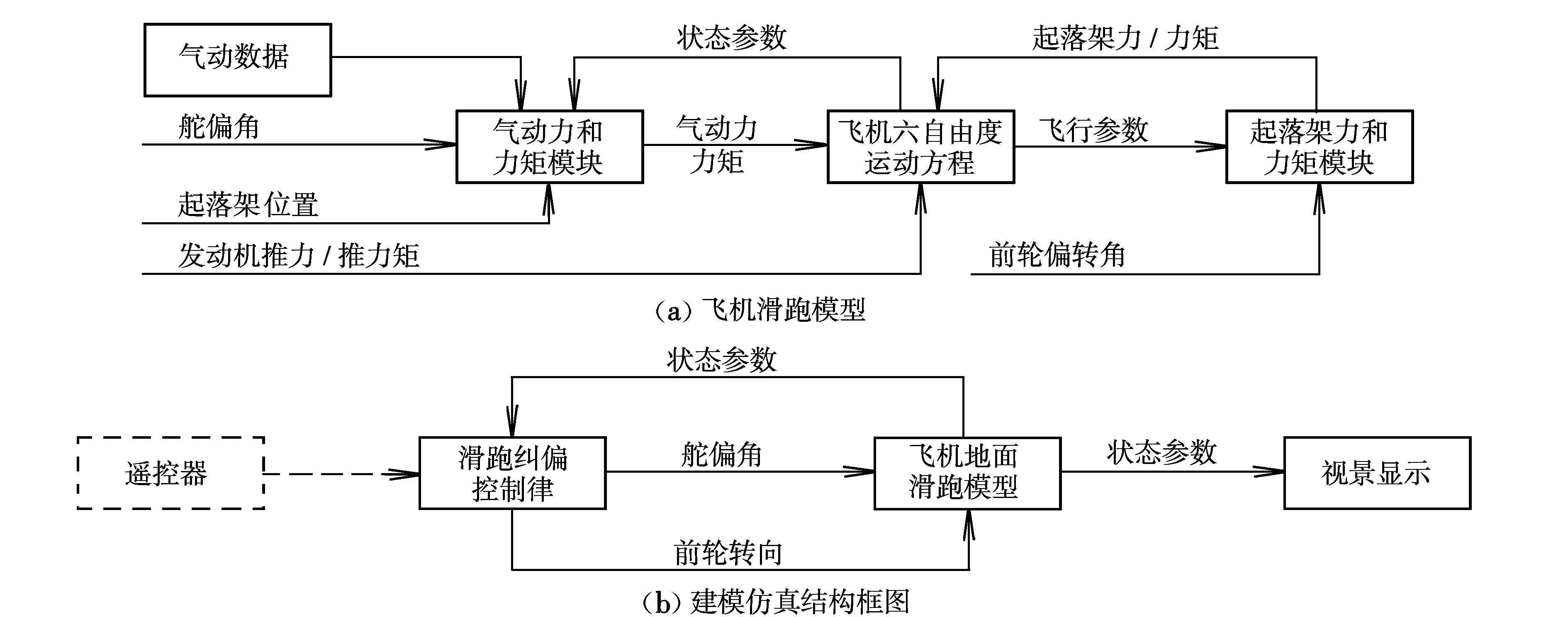
图4 系统仿真示意图Fig.4 Schematic diagram of system simulation

4.2 仿真验证

试验模型的结构参数为:bw=0.98 m;an=0.86 m;am=0.11 m;rw=0.07 m;停机角θs=2.60°;前后轮摩擦力对重心的传动力臂长度Zf=0.43 m;设初始偏差dY0=10 m。滑跑纠偏控制仿真结果如图5所示,其中θL为前轮偏角,drud为方向舵控制量,dY为侧偏距,dψ为航向偏差。

仿真结果表明,滑跑纠偏控制律能操纵前轮和方向舵偏转,消除侧偏,保持正确的滑跑航向,在受到阶跃干扰时,整个控制过程平稳,无超调、振荡现象。

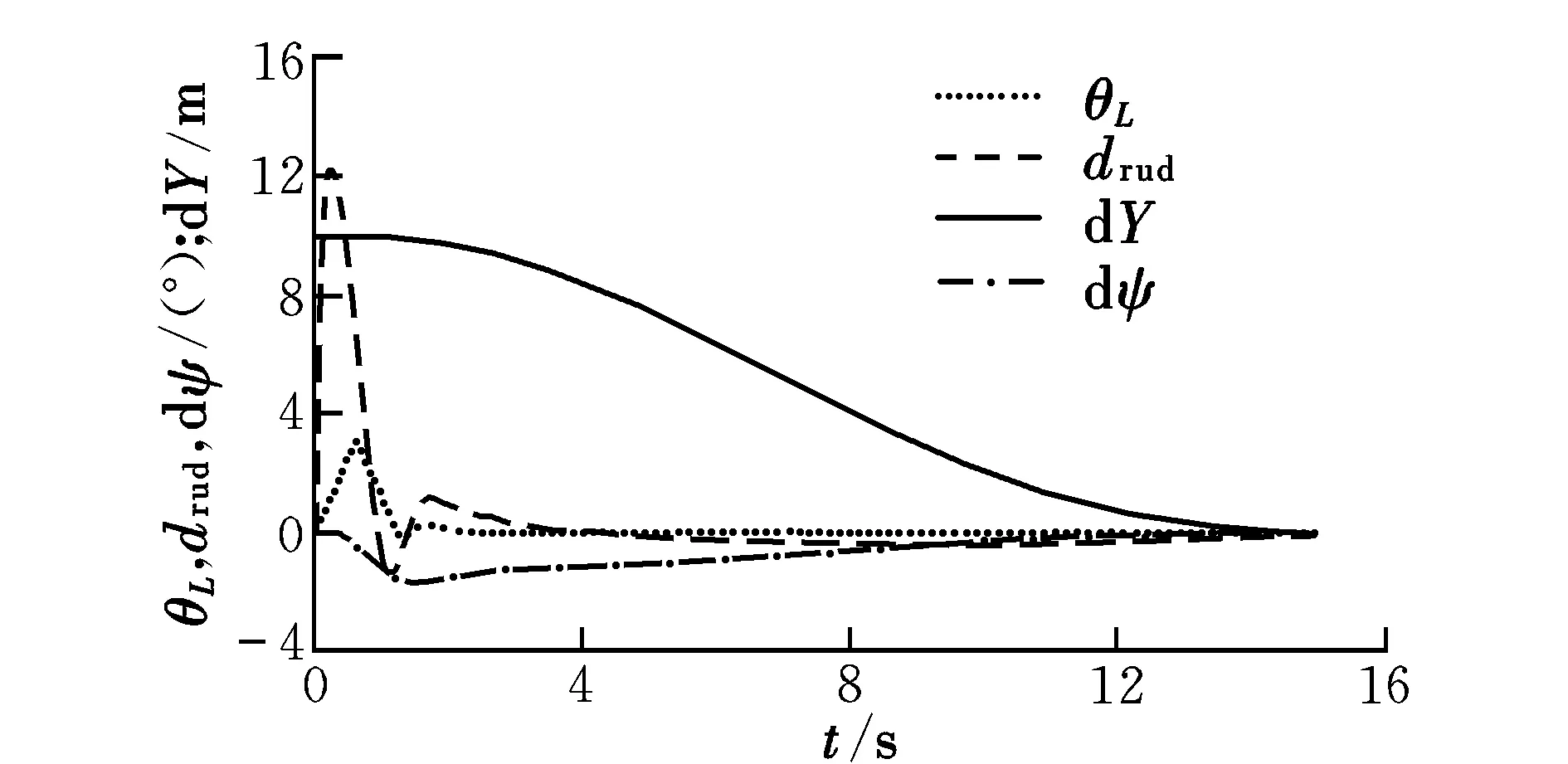
图5 滑跑纠偏控制仿真结果Fig.5 Simulation results of ground taxiing control

5 飞行试验验证

基于设计的滑跑纠偏控制系统,完成了某型战机缩比模型的带动力自主起飞/降落试验科目,起飞和着陆阶段滑跑纠偏效果如图6所示。

飞行试验时跑道上有6 m/s以上的侧风,飞机于40 m/s时离地,地面滑行阶段的最大侧偏距为3 m;飞机接地滑行后,最大侧偏距为2 m。滑跑纠偏控制系统空地状态切换平稳,在低速和高速阶段均具有良好的控制效果。

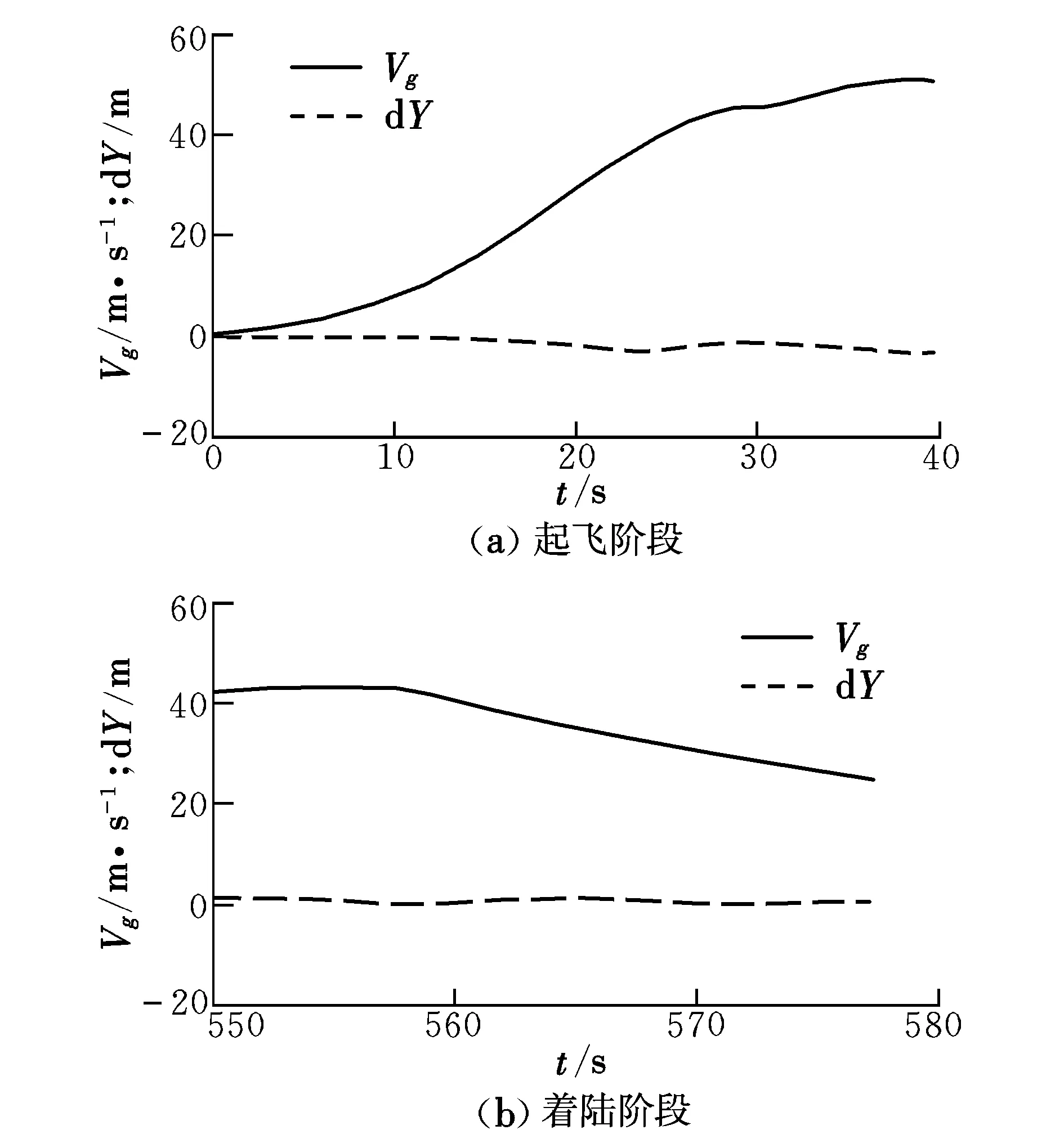
图6 飞行试验滑跑纠偏控制结果Fig.6 Flight test results for deviation-correction in ground taxiing

6 结束语

本文对某型飞机模型飞行试验地面滑跑纠偏进行了系统研究,分析了试验模型在三轮滑跑和两轮滑跑阶段受力情况,并在此基础上设计了副翼、方向舵与前轮联动的控制策略。仿真与试验结果表明,该控制系统能兼顾低速和高速滑跑纠偏效果,鲁棒性好,能克服跑道不平、飞机结构不对称、外界风干扰、发动机推力不对称等因素,保证试验模型在地面滑跑时沿跑道中心线滑跑。

[1] 张守言,惠宇昕,蔡金狮,等.模型飞行试验[M].北京:国防工业出版社,2002.

[2] 李峰,曹云峰,曹美文.某型无人机着陆过程中地面滑行段的建模与仿真[J].指挥控制与仿真，2006, 28(2):91-94.

[3] Lungu M.The influence of the wind shears and sensor errors upon aircrafts landing process[J].Wseas Transactions on Advances in Engineering Education,2010,7(12):381-392.

[4] 邱东海,马伍元,段镇,等.无人机地面操纵转弯特性分析与计算研究[J].飞行力学,2015,33(4):310-314.

[5] 贺成龙,陈欣,李春涛.无人机地面滑行自主起飞的建模与控制[J].航空学报,2008,29(S1):215-217.

[6] 李峰.某型号无人机起飞、着陆仿真系统研究[D].南京:南京航空航天大学,2006.

[7] 王孝英,诸德培.飞机操纵前轮转弯运动的数学模型及数值计算[J].应用力学学报,1997,14(4):46-50.

[8] 郝现伟,杨业,贾志强,等.无人机着陆滑跑数学模型与纠偏控制[J].电机与控制学报,2014, 18(5):85-91.

[9] 董健康,王洁宁,王安国,等.飞机推出和跑道掉头滑行行为计算方法[J].航空学报,2012,33(12):2183-2191.

[10] 钱小妹.飞机操纵前轮转弯特性仿真研究[D].南京:南京航空航天大学,2008.

(编辑：方春玲)

Research on ground taxiing of an aircraft model fight test

LIU Jin, YE De-zhang, FANG Gui-cai, JIA Tao

(Computational Aerodynamics Institute, China Aerodynamics Research and Development Center, Mianyang 621000, China)

Many factors can result in the deviation of aircraft during the ground taxiing, such as the engine mounting deviation, crosswind disturbance, roughness of runway, structural asymmetry,etc. The purpose of offset-correction control is to keep the aircraft taxiing along the runway center. Firstly, the ground dynamic equation is given, and then stress analysis are studied both in three-wheel taxiing phase and two-wheel taxiing phase. Secondly, a combined-control method using aileron, front-wheel and rudder is designed based on the previous theoretical analysis. Finally, the ground taxiing nonlinear model is established in the environment of Simulink, and the simulation is conducted to validate the control strategy. The flight test results have indicated that switching process of ground-air modes is smooth, and the deviation-correction control system has good performance at both low speed and high speed taxiing course.

model fight test; ground taxiing; dynamic model; deviation-correction control

2016-04-07;

2016-09-05;

时间:2016-09-22 14:55

国家973计划资助项目(613221)

刘进(1984-)，男，四川仁寿人，博士，研究方向为飞行控制系统设计。

V249.1

A

1002-0853(2016)06-0086-04