深度自编码观测器飞机操纵面快速故障诊断

温博文, 董文瀚, 解武杰, 马骏

(空军工程大学 航空航天工程学院, 陕西 西安 710038)



深度自编码观测器飞机操纵面快速故障诊断

温博文, 董文瀚, 解武杰, 马骏

(空军工程大学 航空航天工程学院, 陕西 西安 710038)

为了避免扩展多模型自适应估计故障诊断方法中的雅克比矩阵计算,解决飞机精确模型难以获得的问题,降低在线故障诊断的计算量,提出了一种基于深度自编码观测器的飞机操纵面快速故障诊断方法。基于离线训练、在线估计的思想,采用量测的飞行数据训练得到不同故障下的飞机模型,代替扩展多模型自适应估计方法的卡尔曼滤波器进行状态估计;基于基础自编码器的隐层节点数选取经验公式,推导了两种深度自编码器的隐层节点数选取的递推公式。仿真结果表明,该方法无需精确的飞机模型,故障诊断速度快、精度高。

飞机操纵面故障; 状态估计; 深度学习; 故障诊断

0 引言

操纵面是飞行控制系统中最重要的组成部分之一。飞机在飞行过程中会受到外界环境的影响,尤其是战斗机在战斗过程中将不可避免地产生各种操纵面故障,严重威胁飞行安全。因此,飞机操纵面故障诊断至关重要[1]。在能够获得系统精确数学模型的情况下,多模型自适应估计方法是针对飞机操纵面故障的一种有效、快速的故障诊断方法[2];但是,该方法需要预先建立精确的数学模型,飞机发生故障时模型即发生变化。为了解决飞机模型具有高度非线性且难以获得的问题,基于数据知识的神经网络故障诊断方法成为研究的热点[3]。Hinton等[4]提出了逐层训练参数的思想,解决了多隐层神经网络参数初始化问题。对于高度复杂的非线性函数,深度模型比浅层模型具有更强的表达力,展现了强大的从少数样本集中学习数据集本质特征的能力[5-6]。利用深度模型来描述数据间的复杂关系,能够克服浅层学习算法的局限性,提高复杂函数表征能力[7]。同时,网络的拓扑结构直接影响学习能力和信息处理能力,因此研究人员高度重视隐层节点的选择。隐层节点数与输入输出单元数量有着密切联系[8]。隐层节点数对网络性能有巨大影响,节点数越多,学习时间越长;但是节点数太少会导致网络的容错性能较差[9]。目前,大多数研究者基于经验或大量试验结果选择节点数,还没有一种自编码优化的方法来选择最优的网络结构。

本文针对飞机操纵面的典型故障,提出了一种基于深度自编码优化(Deep Auto-Encoder,DAE)的多模型深度学习快速故障诊断方法,并仿真验证了该算法的有效性。

1 基于深度学习多模型的故障诊断方法

飞机非线性离散动力学方程为[10]:

(1)

其中:

x=[p,q,r,α,β]T

u=[δal,δar,δel,δer,δr,FT]T

基于深度自编码优化的多模型快速故障诊断方法如图1所示。这需要训练i+1个DAE观测器,用于观测无故障和i种故障模式。

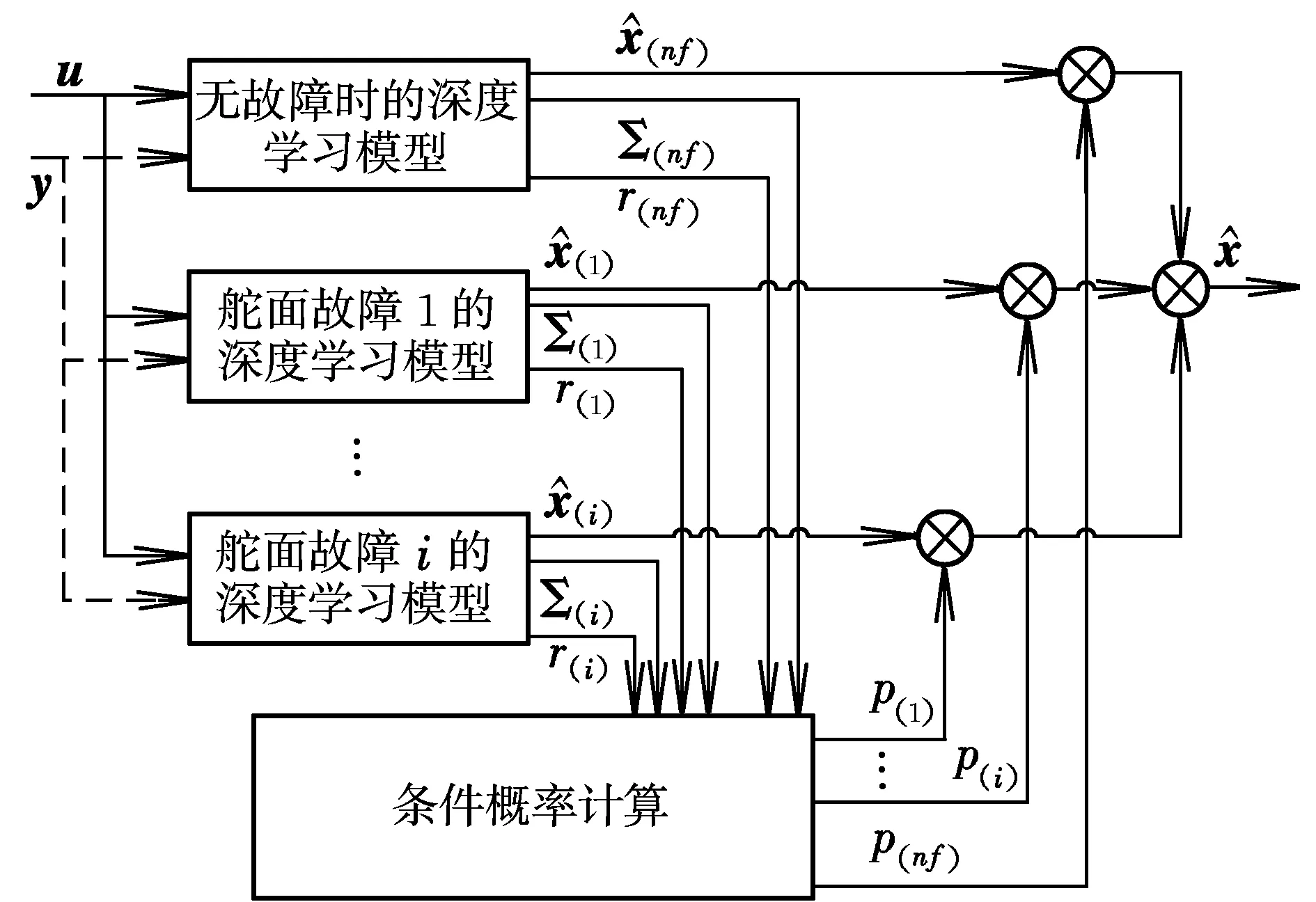
图1 基于深度自编码优化的多模型故障诊断方法Fig.1 DAE based multiple-model diagnosis algorithm

2 深度自编码观测器

深度神经网络模型使用BP算法训练网络模型时,常常会陷入局部最小值。无监督贪婪地逐层参数初始化是深度学习的核心思想。通过无监督初始化的参数代替BP中随机初始化值,有助于权值处于参数空间中较好的位置,避免陷入局部最小值。

为了解决深度网络模型训练的问题,利用自编码进行权值参数初始化,然后利用反向传播算法进行微调。训练步骤如下:

步骤1:归一化训练数据,并利用自编码初始化网络参数。

自编码器是一种尽可能复现输入信号的神经网络[5]。传统编码器表示为:

(2)

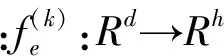
sigmoid(x)=1/(1+exp(-x))

(3)

(4)

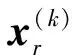
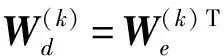
(1)初始化深度网络参数W(1)。第1个自编码网络的输入为飞机的控制输入向量u,则用训练后的W(1)代替深度结构网络随机初始化的参数W1;

(2)初始化网络参数W(k)。训练第k个自编码时,网络的输入为第k-1个自编码网络隐层的输出。用训练后的参数W(1),W(2),…,W(k-1)代替初始化参数Wk,并计算隐层输出;

(3)重复(2)至优化完第n-1个网络参数;

(4)最后一层输入作为监督层的输入。

步骤2:采用批量梯度下降法,对整个网络参数进行有监督的微调。

DAE观测器必须经过参数调优,一般选择BP算法进行调整。调整的核心是把输入层、输出层、隐层看作一个整体,通过有监督的学习调整网络。经过多次训练后,误差和权值达到最优。其过程为:

(1)对权值、误差、阈值初始化;

(2)基于BP算法,用训练集训练网络并计算每一层的输出;

(3)计算每层的重构误差并调整权值和偏差;

(4)重复(2)～(3),直到整个网络的输出满足性能要求。

定义如下深度神经网络的代价函数:

J(θ)=JMSE(θ)+Jweight(θ)

(5)

其中:

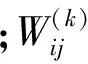
Jweight(θ)限制权值在一个很小的范围内以避免过拟合。因此,循环一次参数W,b的更新公式为:

(6)

式中:η为学习速率。

根据反向传播算法,代价函数可由下式计算:

(7)

定义输出层第i个节点的误差项为:

‖y-h(x)‖2

(8)

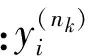
定义第k层第i个神经元节点的输出误差项为:

(9)

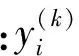
根据反向传播算法,第k层代价函数对参数W,b的偏导数为:

(10)

将式(10)代入式(7),经过一定次数的循环更新,即可得到优异的网络参数W,b。

3 深度自编码观测器隐层节点数选择

深度自编码观测器的模型结构,如隐层数以及隐层节点数,对于重构性能至关重要。本文根据3层神经网络隐层节点数选择的经验公式,推导了两种隐层节点数选择的递推公式。

在N层DAE观测器的预处理过程中,每一隐层是一个基础自编码器,如图2(a)所示。一个基础的自编码器由3层神经网络构成,是一种简单的包含一个隐层的神经网络,能够像编码器一样重构输入。图2(b)为两层自编码器。

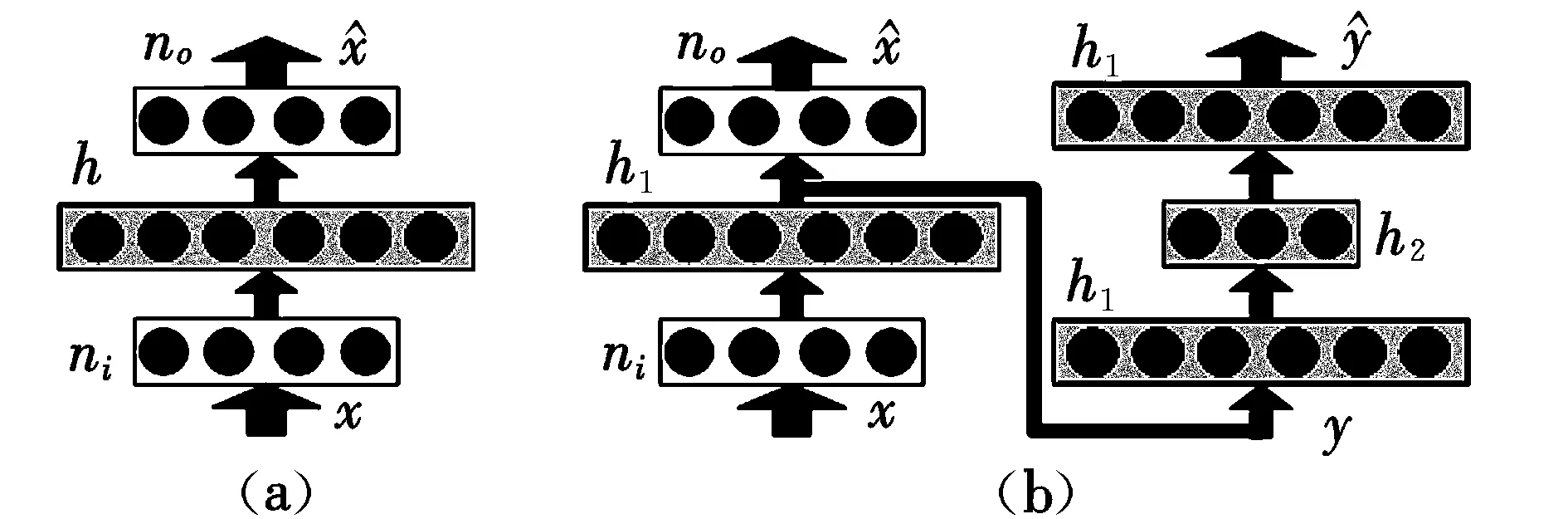
图2 自编码器结构Fig.2 Structure of auto-encoder

图中:ni,no分别为输入层节点、输出层节点;hk为第k层节点。如ni+h1+h2+no代表一个输入层为ni、输出层为no、隐层节点为h1和h2的深度网络。

对于任一个自编码器,隐层节点h可以通过3层神经网络的经验公式来选择,即:

(11)

h=

(12)

第k隐层自编码器的输入为上一隐层的输出,即第k层的输入ni为前一隐层节点数hk-1,因此可以通过以下两种迭代公式计算第k层节点数:

(13)

(14)

第一隐层的输入为系统输入ni,即h0=ni。

4 仿真验证

4.1 仿真条件

仿真中,对文献[10]中的六旋翼非线性模型采用PID控制,并且加入传感器的量测噪声,噪声模型均值为0.001的白噪声。利用Matlab进行数据采集,包括需要的正常数据和故障数据。训练数据的采样时间为90 s,采样周期为0.01 s,共9 001组样本。无故障数据采集时,选取正常状态下的飞机控制输入和实际输出,输入的方波信号分别为:(1)t=0～20 s,俯仰角跟随频率0.1 Hz,振幅15°;(2)t=30～50 s,滚转角跟随频率0.08 Hz,振幅10°;(3)t=60～80 s,偏航角跟随频率0.06 Hz,振幅12°。

4.2 DAE观测器结构选择及训练结果

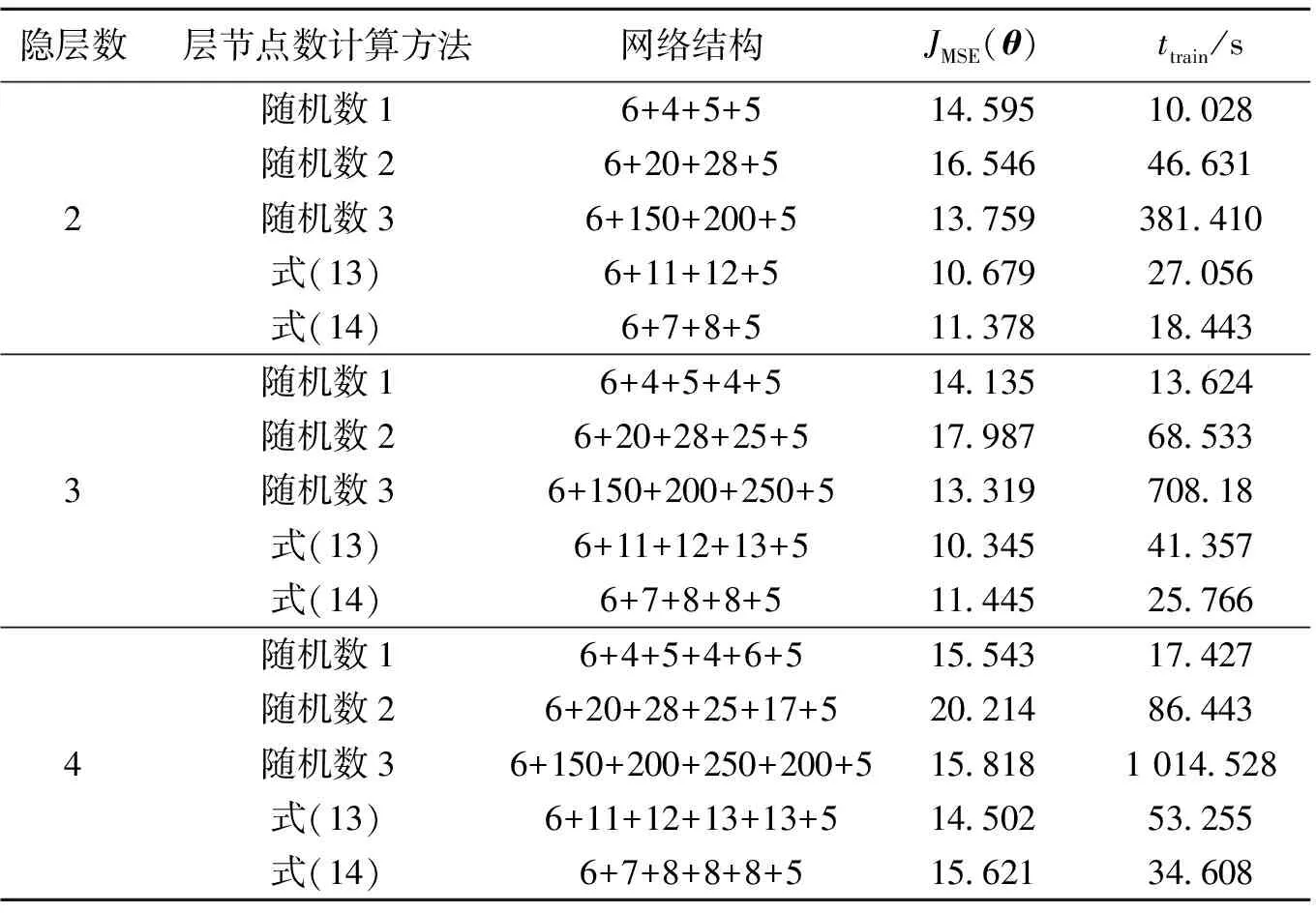
表1为不同网络结构的试验结果,通过改变隐层节点数和隐层数来评估DAE观测器的性能。

表1 不同结构的DAE观测器仿真结果

Table 1 Simulation results of different DAE structures

隐层数层节点数计算方法网络结构JMSE(θ)ttrain/s2随机数16+4+5+51459510028随机数26+20+28+51654646631随机数36+150+200+513759381410式(13)6+11+12+51067927056式(14)6+7+8+511378184433随机数16+4+5+4+51413513624随机数26+20+28+25+51798768533随机数36+150+200+250+51331970818式(13)6+11+12+13+51034541357式(14)6+7+8+8+511445257664随机数16+4+5+4+6+51554317427随机数26+20+28+25+17+52021486443随机数36+150+200+250+200+5158181014528式(13)6+11+12+13+13+51450253255式(14)6+7+8+8+8+51562134608

可以看出,网络结构采用6+11+12+13+5能够得到最佳性能。其中，6为输入层节点数;11,12,13分别为隐层h1,h2,h3的节点数;5为输出层节点数。随机节点数的性能是不稳定的:节点数越少,训练结果均方误差越大;节点数越多,训练时间越长。本文方法节点数选择精度高、训练时间短。

图3给出了无故障情况下调优过程代价函数收敛图。可以看出,在训练循环2 000次左右时,基本收敛到恒定值。此时可以认为网络参数为最优参数。本文方法选择的网络结构收敛速度最快。

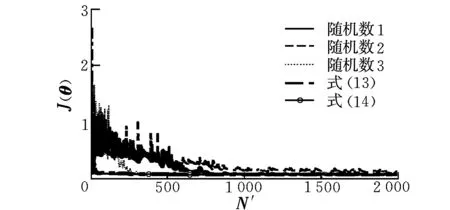
图3 代价函数收敛曲线Fig.3 Convergence curves of cost function

图4给出了无故障情况下,利用操纵系统各操纵面无故障时的数据对网络进行测试,侧滑角的DAE观测器训练结果。可以看出网络输出值与真实值拟合良好,说明所建立的网络可靠。

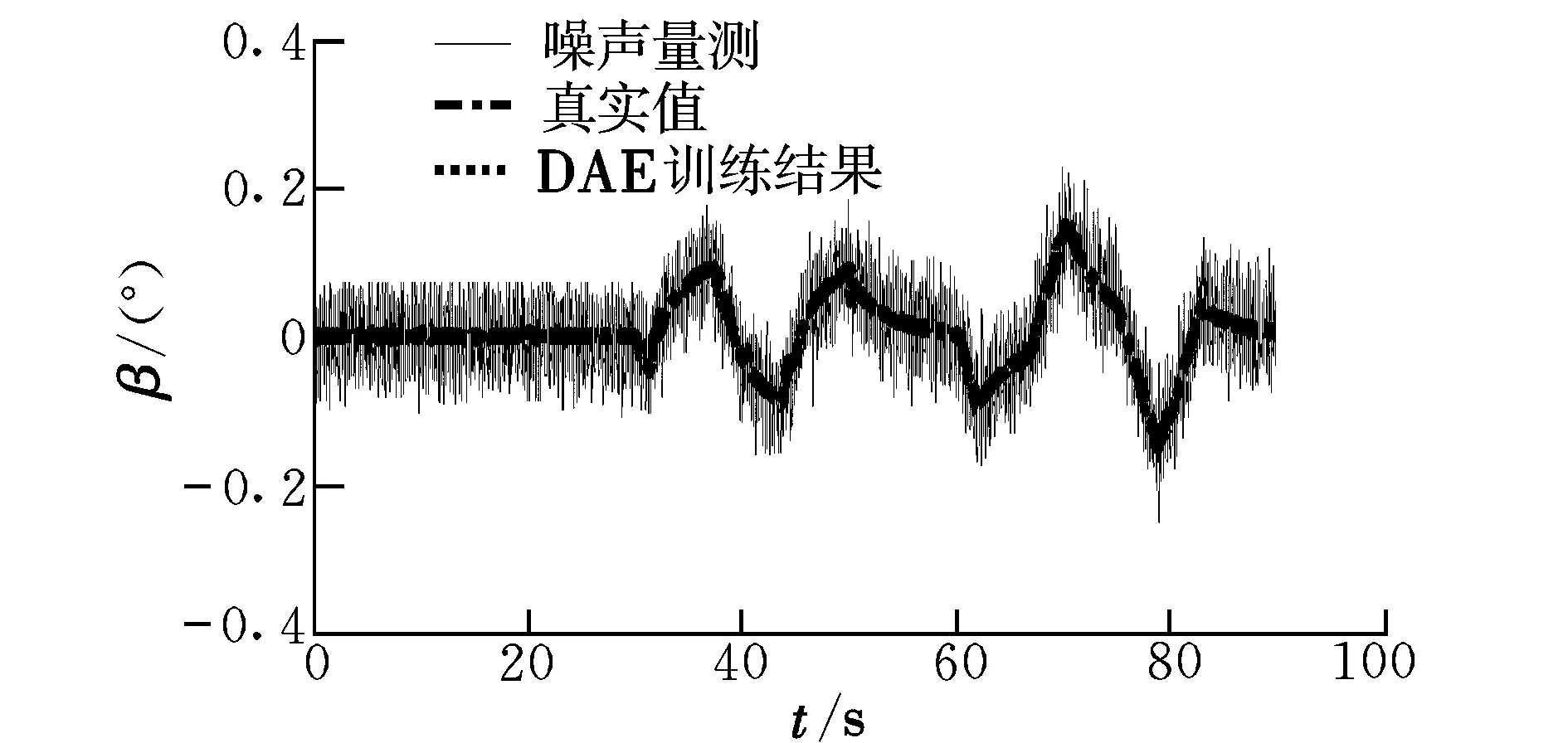
图4 无故障时侧滑角DAE观测器训练结果Fig.4 Training results of DAE observer for sideslip angle without fault

4.3 典型故障诊断仿真验证

训练后,DAE观测器的参数θ固定不变,并作为深度学习故障诊断系统的输入。故障诊断仿真共采样300 s:t=10～40 s时，左副翼卡死在20°的位置;t=70～100 s时，右副翼卡死在-15°的位置;t=130～160 s时，方向舵卡死在-2°的位置;t=190～220 s时，左升降舵卡死在-20°的位置;t=250～280 s时，右升降舵卡死在-15°的位置。

针对一系列故障,利用测试数据对多模型系统进行故障诊断。定义在一段检测时间内,如果故障概率达到90%,则认为操纵面发生故障;如果故障概率不足5%,则认为操纵面正常。图5给出了根据不同的故障检测方法得到的故障概率图。

图5 故障概率Fig.5 Failure probability

由图5可以看出,故障均能被准确诊断,而且比普通的EMMAE方法[10]缩短了故障检测时间。EMMAE方法计算得到的状态估计的均方根误差为40.799 2,测试时间为11.504 5 s;DAE方法均方根误差为13.534 2,测试时间为4.203 4 s。基于DAE观测器的故障诊断方法均方根误差更低,提高了飞行状态的估计精度,降低了故障诊断时间。

图6比较了有噪声和无噪声时的测量结果,给出了基于不同故障诊断方法的概率加权得到的飞机状态估计结果。可以看出,EMMAE 方法[10]得到的状态能够基本拟合真实值;DAE观测器的效果更好,能够较好地拟合真实值。

图6 概率加权状态估计Fig.6 Probability-weighted state estimation

5 结束语

本文提出了一种基于深度自编码观测器的多模型快速故障诊断方法,该方法避免了卡尔曼滤波器雅克比矩阵的计算,无需飞机精确的数学模型,即可诊断飞机操作面的故障,提高了故障诊断的速度和状态估计的精度。后续将进一步研究同时出现多个故障的诊断问题。

[1] Odendaal H M,Jones T.Actuator fault detection and isolation: an optimised parity space approach[J].Control Engineering Practice,2014,26(11):222-232.

[2] Ma J,Ni S,Xie W,et al.An improved strong tracking multiple-model adaptive estimation:a fast diagnosis algorithm for aircraft actuator fault [J].Transactions of the Institute of Measurement and Control,2015,38(7):846-854.

[3] Singh S,Murthy T V R.Neural network-based sensor fault accommodation in flight control system[J].Journal of Intelligent Systems,2013,22(3):317-333.

[4] Hinton G E,Osindero S,Teh Y W.A fast learning algorithm for deep belief nets[J].Neural Computation,2006,18(7):1527-1554.

[5] Liu X,Zhang W,Huang Y,et al.Neural network-based sensor online fault diagnosis and reconfiguration for flight control systems[C]//The Sixth World Congress on Intelligent Control and Automation.Dalian:IEEE,2006:5577-5580.

[6] Yuan H,Lu C,Xiong Z,et al.Fault detection for an aileron actuator under variable conditions based on bi-step neural network[J].Applied Mechanics and Materials,2015,764-765:740-746.

[7] Yuan H,Lu C,Ma J,et al.Neural network-based fault detection method for aileron actuator[J].Applied Mathematical Modelling,2015,39(19):5803-5815.

[8] Napolitano M R,Silvestr G I,Windon D A,et al.Sensor validation using hardware-based on-line learning neural networks[J].IEEE Transactions on Aerospace and Electronic Systems,1998,34(2):456-468.

[9] Zhang G,Wang B.Fault diagnosis of flying control system servo actuator based on Elman neural network[C]//2011 10th International Conference on Electronic Measurement and Instruments (ICEMI).Chengdu:IEEE,2011:46-49.

[10] Ducard G,Geering H P.Effcient nonliner actuator fault detection and isolation system for unmanned aerial vehicles[J].Journal of Guidance,Control,and Dynamics,2008,31(1):225-237.

(编辑：李怡)

Fast fault diagnostic method for aircraft actuators with deep auto-encoder observer

WEN Bo-wen, DONG Wen-han, XIE Wu-jie, MA Jun

(Aeronautics and Astronautics Engineering College, AFEU, Xi’an 710038, China)

To avoid the calculation of Jacobi matrix in traditional multiple model adaptive estimation method, solve the problem of difficult to obtain accurate plane model and reduce the amount of calculation for online fault diagnosis, a deep auto-encoder observer multiple-model fault diagnosis algorithm for aircraft actuator fault was proposed. Based on the thought of off-line training and online estimation, the method replaced Kalman filters in traditional multiple model adaptive estimation with different fault aircraft models obtained by training measured flight data. Based on the empirical formula of the basic auto-encoder hidden layer node number selection, two recursive formulas for deep auto-encoder hidden layer node number selection were derived. The simulation results show that the method does not require accurate aircraft models and has fast speed and high accuracy for fault diagnosis.

aircraft actuator fault; state estimation; deep learning; fault diagnosis

2016-04-29;

2016-07-25;

时间:2016-09-28 09:52

温博文(1992-)，男，四川眉山人，硕士研究生，主要研究方向为数据处理。

V249.1

A

1002-0853(2016)06-0034-05