六旋翼无人机的飞行力学建模研究

辛冀, 董圣华, 刘毅, 陈仁良

(1.中航工业直升机设计研究所 总体气动室, 江西 景德镇 333001;2.南京航空航天大学 航空宇航学院, 江苏 南京 210016)



六旋翼无人机的飞行力学建模研究

辛冀1, 董圣华1, 刘毅1, 陈仁良2

(1.中航工业直升机设计研究所 总体气动室, 江西 景德镇 333001;2.南京航空航天大学 航空宇航学院, 江苏 南京 210016)

为开展六旋翼无人机的全机飞行力学建模研究,针对六旋翼无人机的前飞和非定常飞行要求,引入了动量叶素理论和动态入流理论对旋翼气动力进行分析。根据无人机的变转速控制方式,增加了旋翼转速变化对机身运动的影响项,推导了使六旋翼总需用功率最小的拉力分配优化方法,建立了六旋翼无人机的飞行力学模型。气动力计算结果表明,新建立的旋翼气动力计算方法精度高于现有的比例系数法。

六旋翼; 无人机; 飞行力学模型; 飞行模态

0 引言

六旋翼无人机将6个旋翼布置在一个六边形的顶点位置上,采用6个旋翼的拉力作操纵力。6个旋翼的旋转方向不同,通过改变旋翼转速来改变无人机的姿态和位置。六旋翼无人机具有两个冗余的操纵量,当遇到强外力干扰或部分旋翼受损时仍具有良好的稳定性和安全性,更适合在危险和恶劣的环境下工作。

目前国内的六旋翼无人机产品还不多,理论研究也刚刚起步,主要是对相应的飞控系统开展研究[1-3]。在六旋翼无人机飞行力学建模中还很少考虑自由来流和非定常飞行对旋翼气动力的影响[4-6],建模精度低,适用范围窄。随着对六旋翼无人机飞行性能和机动能力要求的提高,在无人机控制律设计中对飞行力学模型的依赖必将日益增强,因而急需开展精度高、适用范围广的六旋翼无人机飞行力学建模研究。

本文采用叶素理论计算旋翼气动力,并加入旋翼的动态入流效应,提高了旋翼气动模型对瞬态运动和前飞状态的分析精度。在此基础上,考虑多种惯性力和重力对无人机的影响,建立了六旋翼无人机的飞行力学模型,并进行了前飞状态下的配平计算和模态分析。

1 空气动力学模型

本节采用Pitt-Peters动态入流理论[7]和叶素理论建立旋翼的非定常空气动力学模型。仅考虑旋翼的均匀诱导入流部分,如果拉力系数CT相比于某一稳态值出现了一个突变ΔCT,则诱导速度v0的改变量Δv0满足式(1)中的微分方程[8]。

(1)

其中:

[L]=

α=arctan[(λ+v)/μ]

式中:λ,μ和v分别为稳态条件下自由来流形成的旋翼入流比、前进比和旋翼诱导速度。

根据式(1)获得了旋翼诱导入流的变化情况,忽略无人机低速飞行状态下的某些小量后,可直接使用叶素理论[9]获得旋翼拉力和反扭矩表达式如式(2)和式(3)所示。

θ1(r/R-0.7)(Ωr)2+

[-vi-V∞sin(-αD)]Ωr}dr

=nb(1/2)ρac{φ7Ω2R3/3+θ1Ω2R3/4-

0.7θ1Ω2R3/3+[-vi-V∞sin(-αD)]ΩR2/2}

(2)

(1/Ω)[φ7Ω2r2+θ1(r/R-0.7)(Ωr)2+

(-vi-V∞sin(-αD))Ωr]+

(1/2)ρΩ2Cdcr3}dr

= (1/2)nbρac[vi+V∞sin(-αD)]×

(1/Ω)[φ7Ω2R3/3+Ω2θ1R3/4-

0.7θ1Ω2R3/3+(-vi-V∞sin(-αD))Ω/2]+

(1/2)nbρΩ2CdcR4/4

(3)

式中:nb为旋翼桨叶片数;V∞为自由来流的速度值;αD为桨盘迎角。

已发表的多旋翼无人机旋翼气动性能试验还很少,下面根据文献[10]对不同转速下悬停旋翼的气动力测量结果,验证式(2)和式(3)的准确性。翼型NACA0012的旋翼参数如表1所示,旋翼拉力和需用功率的计算结果与试验值对比如图1和图2所示。图中还给出了仅保留Ω2项的其他文献常用简化公式的计算结果。

表1 旋翼桨叶几何参数

Table 1 Geometry parameters of rotor blade

参 数数值旋翼半径/m052桨叶片数2桨叶弦长/m0033扭转角/(°)-18

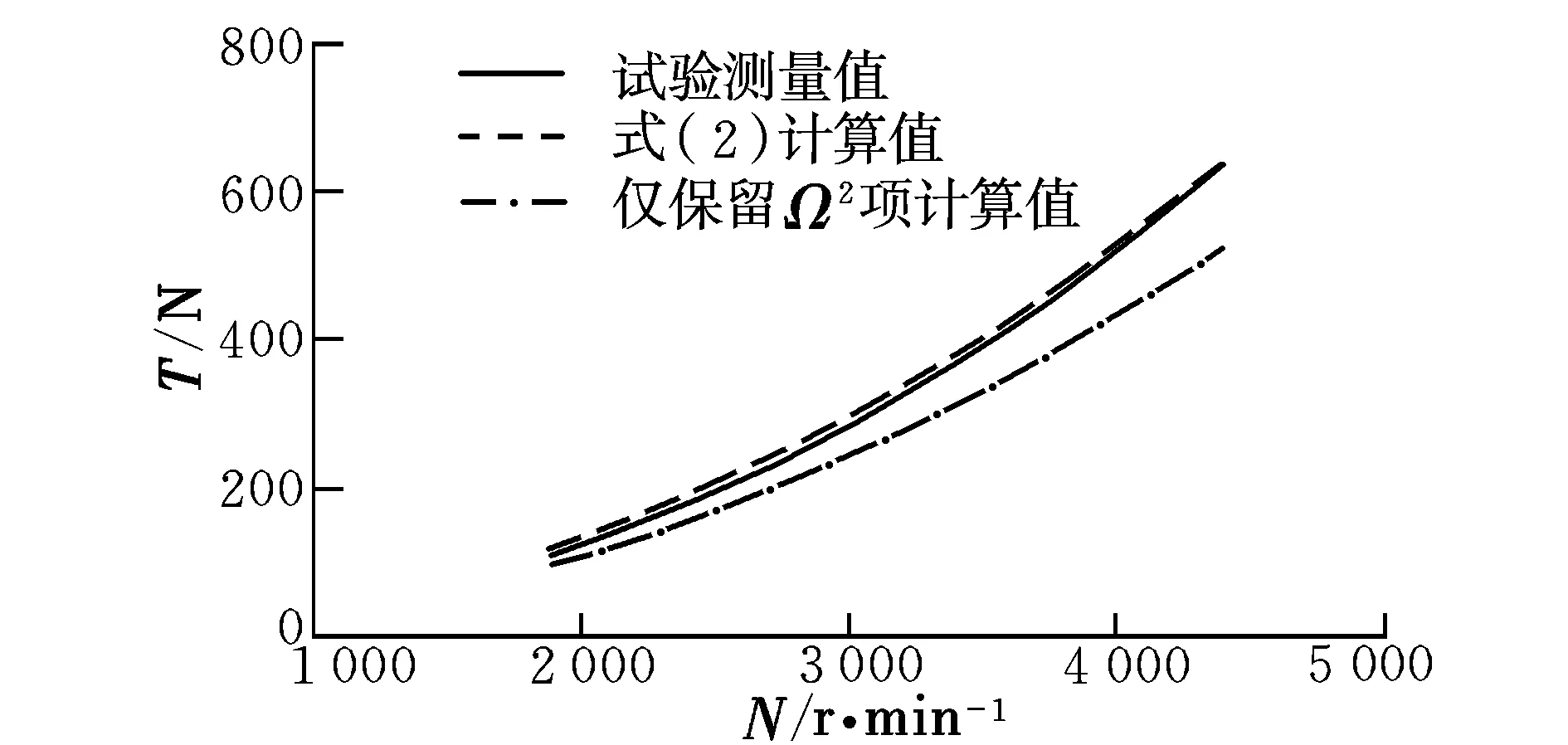
图1 旋翼拉力随转速变化的计算结果与试验值对比Fig.1 Comparison of the analyzed and experimental value of rotor thrust

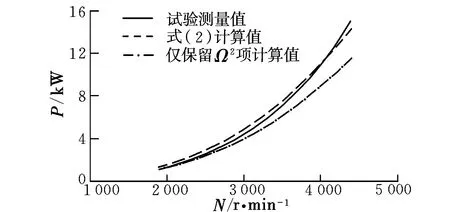
图2 旋翼需用功率随转速变化的计算结果与试验值对比Fig.2 Comparison of the analyzed and experimental value of rotor power

由图可知,使用完整叶素理论表达式计算得到的旋翼拉力和需用功率与试验值符合良好,验证了旋翼气动模型的准确性。仅保留Ω2项的公式在大转速情况下误差则偏大。

除了对悬停状态计算结果不够准确之外,比例系数法还不能考虑旋翼在悬停和前飞状态下气动特性的差别,更无法分析非定常运动对旋翼气动力的影响。而在多旋翼飞行器的配平和运动模态分析中必须考虑到这两方面的问题,需要采用本节所给出的动态入流和叶素理论相结合的方法开展旋翼的气动特性分析。

2 飞行力学分析

2.1 飞行力学建模

基于上一节中的旋翼空气动力学模型,以下对某六旋翼无人机进行飞行力学建模,无人机的主要几何参数如表2所示。

表2 六旋翼无人机的主要几何参数

Table 1 Main geometry parameters of the six-rotor unmanned aerial vehicle

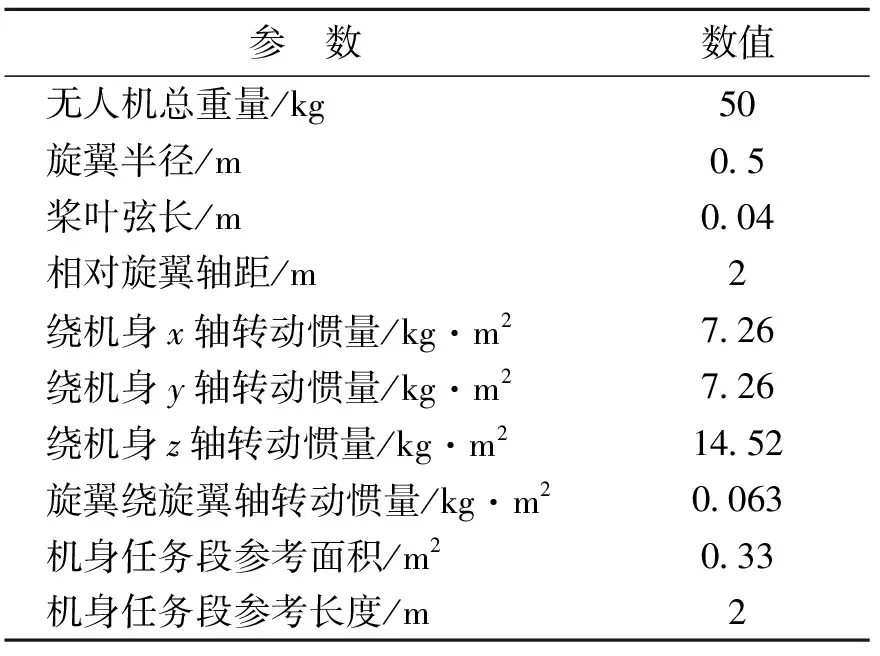
参 数数值无人机总重量/kg50旋翼半径/m05桨叶弦长/m004相对旋翼轴距/m2绕机身x轴转动惯量/kg·m2726绕机身y轴转动惯量/kg·m2726绕机身z轴转动惯量/kg·m21452旋翼绕旋翼轴转动惯量/kg·m20063机身任务段参考面积/m2033机身任务段参考长度/m2

无人机的偏航角ψ、俯仰角θ和滚转角φ与文献[11]中的规定相同。无人机机体坐标系的定义如图3所示。

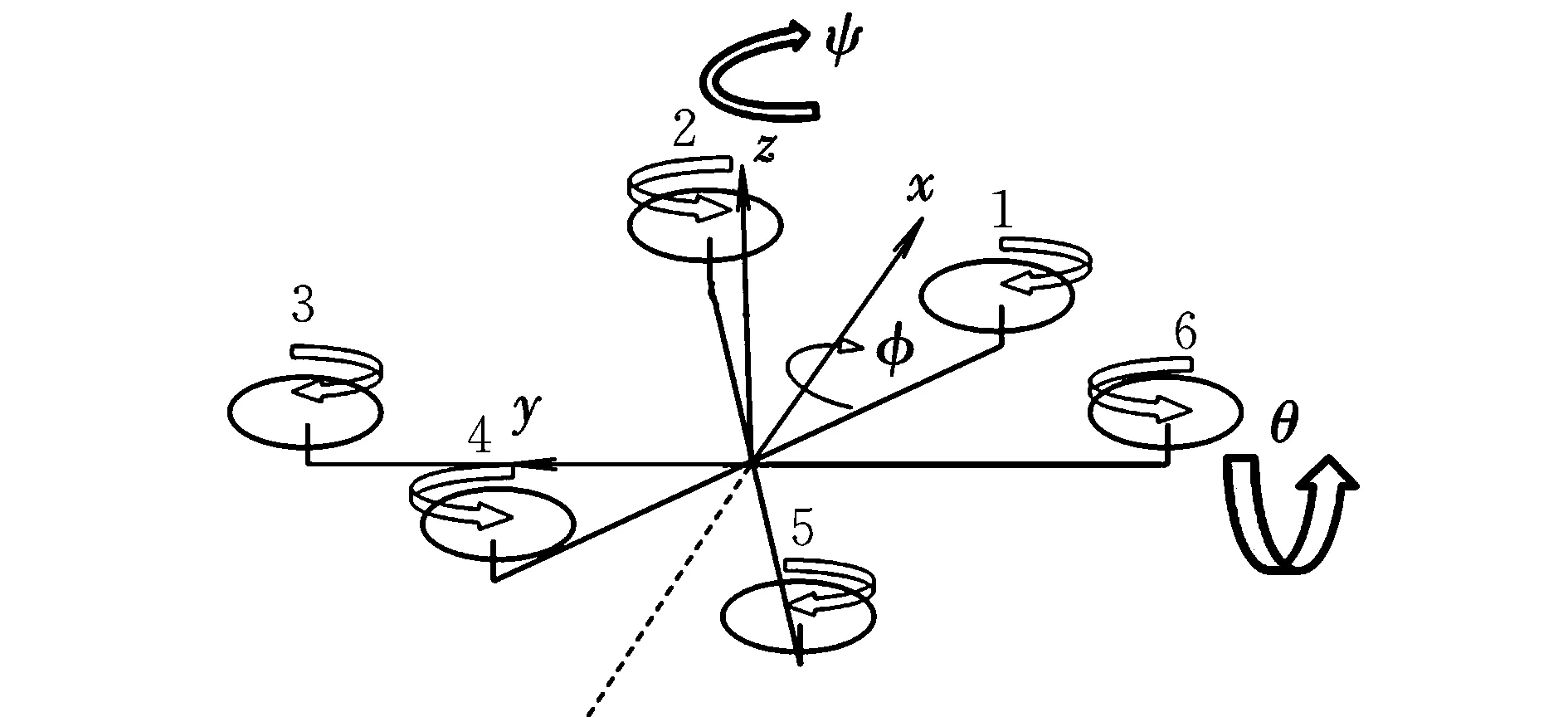
图3 机体坐标系及姿态角示意图Fig.3 The fuselage coordinate and attitude angle

无人机的飞行力学方程组由飞行器沿体轴系3个方向的线运动和角运动方程组成。飞行器质心的线运动动力学方程为:

(4)

式中:I3×3为单位矩阵;Ω3×1=[p,q,r]T为机体坐标系中绕3个轴的转动角速度;V3×1=[u,v,w]T为机体坐标系中3个轴方向上的线速度;F3×1为无人机受到的合力,由重力W、机身升力Tf、阻力Df、侧力Lf和旋翼拉力T相加组成。

飞行器绕质心转动的动力学方程组为:

(5)

式中:J3×3为全机相对于质心的转动惯量矩阵,在无人机相对于x,y,z轴均对称的情况下,J3×3=diag(Jx,Jy,Jz);M3×1为外力对机身质心3个方向的合力矩,包括机身气动力矩、旋翼拉力对质心形成的力矩、旋翼气动反扭矩、旋翼转速改变产生的惯性反扭矩,以及旋翼随机身转动而产生的陀螺力矩。

将上面给出的动力学方程组和3个姿态角的运动学方程组结合,再加入无人机的机身角速度和姿态角速度之间的关系,就得到了关于无人机9个运动状态量X=[u,v,w,p,q,r,φ,θ,ψ]的飞行动力学微分方程组，如式(6)所示。其中,Ti,Qi和ωi分别为第i个旋翼的拉力、反扭矩和转速;Cd,Cc,Cl,Cfφ,Cfθ和Cfψ分别为3个机体轴上的气动力系数和气动力矩系数。

(6)

2.2 六旋翼无人机的平衡

将飞行动力学方程组中的转动角速度、角加速度、线加速度置为0,得到此时的全机六力素平衡方程组如式(7)所示。

(7)

在给定的前飞速度下,将六旋翼的合拉力T、俯仰力矩Mrθ、滚转力矩Mrφ、反扭矩Q,以及机身的俯仰角θ和滚转角φ作为未知量,以Newton-Raphson方法迭代求解平衡方程组。

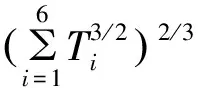
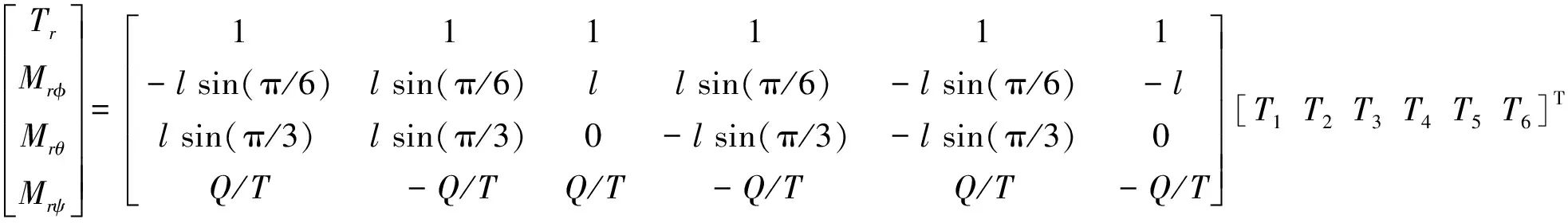
(8)

将上面的系数矩阵表示为Arotor,则上面方程组的最小范数解为:

(9)

然后即可根据各旋翼的拉力,反求6个旋翼的目标转速。

当六旋翼无人机以10 m/s的速度匀速前飞时,配平得到无人机的6个旋翼转速依次为:ω1=253.84 rad/s,ω2=243.80 rad/s,ω3=253.30 rad/s,ω4=243.26 rad/s,ω5=253.32 rad/s,ω6=243.82 rad/s。无人机的俯仰角θ=-1.42°,滚转角φ=0.22°。

2.3 六旋翼无人机的飞行模态分析

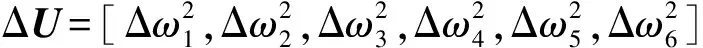
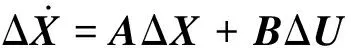
(10)

其中:

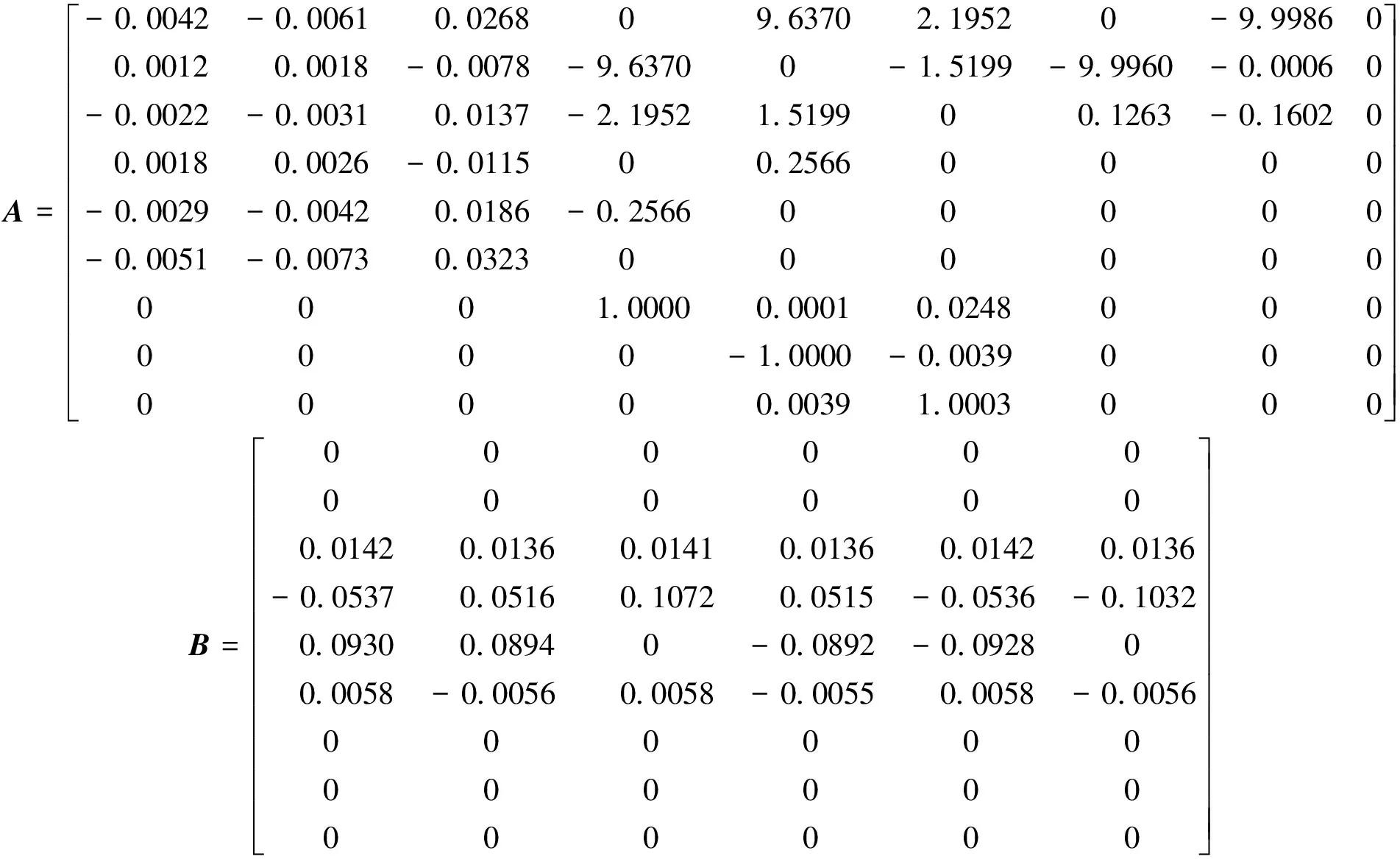
从小扰动线化方程组中得到的状态矩阵特征根和对应的特征向量整理后如下:

(0.1263±0.3932i)～[0.8764,0.1476,0.0122,0.0073,-0.0063,-0.0067,0.0100,-0.0191,0.0203]T;

-0.3583～[-0.2008,-0.9639,0.1308,0.0175,-0.0073,-0.0344,-0.0465,-0.0208,0.0961]T;

0.1311～[0.8267,-0.5612,0.0200,0.0007,0.0011,0.0043,0.0060,-0.0088,0.0327]T;

-0.0143～[0.8572,-0.5095,0.0196,0.0000,0.0000,-0.0010,-0.0006,0.0010,0.0721]T;

-0.0～[0.8614,-0.5076,0.0202,0.0000,0.0000,0.0000,0.0000,0.0000,0.0000]T;

0.0～[-0.8614,0.5076,-0.0202,0.0000,0.0000,0.0000,0.0000,0.0000,0.0000]T;

0.0～[0.3426,-0.6892,-0.1030,0.0000,0.0000,0.0000,0.0000,0.0000,-0.6301]T;

0.0～[-0.0016,0.0033,0.0005,0.0000,0.0000,0.0000,0.0000,0.0000,1.0000]T

可见,有4个模态的特征根为0,这些模态通常是3个方向的速度和偏航角的组合,说明在这样的速度扰动组合情况下,无人机可以达成随遇平衡。六旋翼无人机的随遇平衡模态数量如此之多,应该与其高度的几何对称性有关。

第4个模态对应于一个较大的正特征根,是非周期发散模态。取该模态特征向量中的纵向通道状态量进行分析可以看出,当速度u为正值时,俯仰角速度q为正值、俯仰角θ为负值,参考图4,这种运动会促进前飞速度V∞和u的增长。而当u增加时,由式(2)可知,各旋翼的拉力又会增大,其中原先转速高、拉力大的旋翼拉力增幅最大,使无人机的角速度进一步增加,俯仰姿态进一步低头,最终导致纵向通道的发散。同理分析可知,模态中的横向通道滚转运动也是发散的。究其发散原因,是因为旋翼桨叶无挥舞运动、空速稳定性差而引起的。

第1个模态为一对实部为正值的共轭复根,处于振荡发散状态。在该模态中,当速度u为正值时,q为负值、θ为负值,θ使u增加,但q使θ和u逐渐减小,θ的作用较为明显,使模态振荡发散。在此过程中q的振幅较小是因为多旋翼本身就可产生俯仰阻尼的作用,而模态中u产生的自由来流对不同转速旋翼造成的影响,又会使该俯仰阻尼进一步增大。

发散运动模态的存在说明在六旋翼无人机的飞行中,需要增稳控制系统对其进行不断的控制调整。

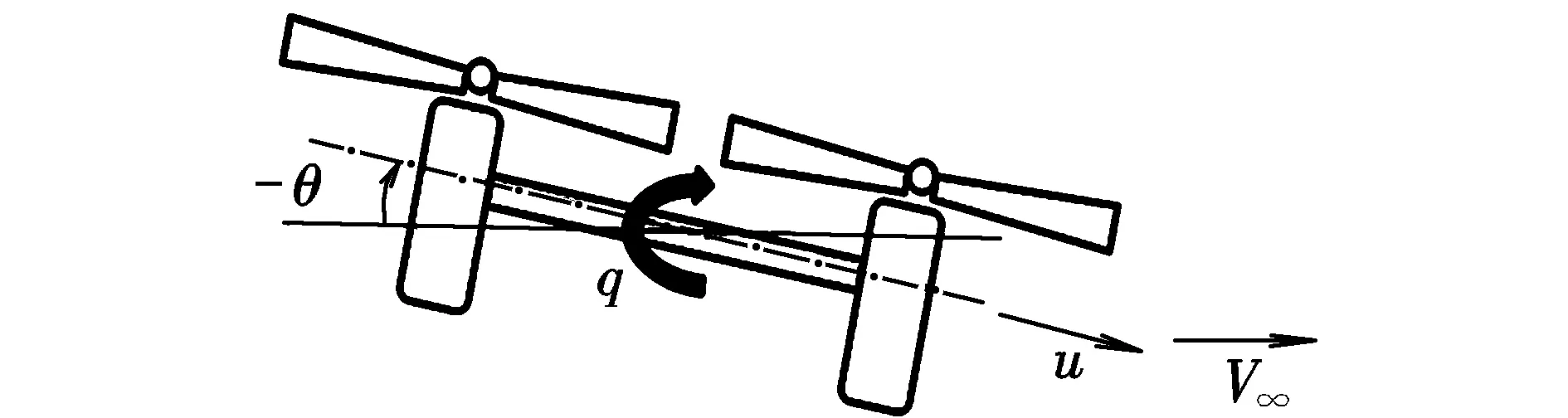
图4 无人机前飞时纵向运动示意图Fig.4 Schematic diagram of the longitudinal motion of a forward flying unmanned aerial vehicle

3 结论

本文建立的六旋翼无人机的飞行力学模型既能指导六旋翼无人机的总体气动设计,也可为其飞控系统的设计与仿真提供更强的支持。经过分析得到以下结论:(1)动态入流理论与叶素理论结合后形成的旋翼气动分析模型,具有计算前飞和瞬态运动状态下旋翼气动力的功能。在悬停状态下的计算精度也优于传统的比例系数法；(2)根据飞行力学建模分析结果,由于六旋翼无人机具有轴对称的几何特点,使其拥有多个随遇平衡运动模态,同时也具有不稳定的运动模态,需要增稳系统辅助其飞行。

[1] Yin L L,Shi J S,Huang Y M.Modeling and control for a six-rotor aerial vehicle[C]//Proceedings of the International Conference on Electrical and Control Engineering.America:IEEE,2010:1289-1292.

[2] 王伟,邱启明.六旋翼飞行器建模及位置跟踪控制[J].电子器件,2014,37(3):507-513.

[3] 杨成顺,杨忠,许德智,等.新型六旋翼飞行器的轨迹跟踪控制[J].系统工程与电子技术,2012,34(10):2098-2105.

[4] 花寅.六旋翼无人机直升机控制技术研究[D].南京:南京理工大学, 2013.

[5] 高翔.六旋翼无人机的设计[D].哈尔滨:哈尔滨工业大学,2014.

[6] 单海燕.四旋翼无人直升机飞行控制技术研究[D].南京:南京航空航天大学,2008.

[7] Pitt D M,Peters D A.Theoretical prediction of dynamic inflow derivation[J].Vertica,1981,5(1):21-34.

[8] 孙文胜.基于动态入流的无人直升机操纵特性研究[J]. 航空计算技术,2003,33(2):45-47.

[9] Leishman J G,Bhagwat M J,Bagai A.Free-vortex filament methods for the analysis of helicopter rotor wakes[J].Journal of Aircraft,2002,39(5):759-775.

[10] Bouabdallah S,Siegwart R.Backstepping and sliding-mode techniques applied to an indoor micro quadrotor[C]//Proceedings of the 2005 IEEE International Conference.England:IEEE,2005:2247-2252.

[11] 陈仁良. 直升机飞行动力学[M]. 北京: 科学出版社, 2003.

(编辑：方春玲)

Flight dynamics modeling research for a six-rotor unmanned aerial vehicle

XIN Ji1, DONG Sheng-hua1, LIU Yi1, CHEN Ren-liang2

(1.General Design Department, AVIC Helicopter Research and Development Institute, Jingdezhen 333001, China; 2.College of Aerospace Engineering, NUAA, Nanjing 210016, China)

A research on the flight dynamics modeling of a six-rotor unmanned aerial vehicle(R6UAV) was carried out in this paper. The momentum-blade element theory and dynamic inflow theory were incorporated into the rotor aerodynamic analyzing model with respect to the demand for transient flight. The influence of rotor angle acceleration on fuselage was added into the flight dynamic model of R6UAV, and an optimum thrust distribution method was conducted which could give a minimum power. The predicted results indicate that the new founded analysis method for rotor aerodynamic force is more accurate than former proportional prediction method.

six-rotor; unmanned aerial vehicle(UAV); flight dynamics model; flight mode

2016-03-11;

2016-08-10;

时间:2016-09-22 14:55

辛冀(1988-)，男，黑龙江鸡西人，工程师，博士，研究方向为直升机飞行力学。

V212.4

A

1002-0853(2016)06-0010-05