基于MESE的导弹仿真数据一致性验证

赵彬, 周中良, 王金福

(空军工程大学 航空航天工程学院, 陕西 西安 710038)



基于MESE的导弹仿真数据一致性验证

赵彬, 周中良, 王金福

(空军工程大学 航空航天工程学院, 陕西 西安 710038)

以某型空空导弹为对象,对该导弹模型的仿真可信度评估方法进行了研究,提出了基于最大熵谱估计法的导弹仿真数据一致性验证方法。模拟外场试验场景进行了全体系实战对抗仿真试验,并将试验数据作为仿真数据一致性验证的参考数据;对导弹仿真试验的随机动态数据平稳化预处理后,进行了基于最大熵谱估计法的导弹仿真随机动态数据一致性验证。结果表明,该导弹模型具有良好的动态一致性,所提方法可行、有效。

导弹仿真; 平稳化; 最大熵谱估计法; 一致性验证

0 引言

对于高度信息化的现代局部战争,空空导弹作为空战中最常用的武器之一,在制空权争夺过程中发挥着巨大的作用[1-2]。导弹仿真可信度评估是开展空空导弹建模与仿真工作必须解决的问题之一,是判断导弹仿真是否具有应用价值和保证其质量的重要手段;而一致性验证在其可信性评估中起到相当重要的作用。随着建模与仿真技术在导弹研制过程中的广泛应用,导弹仿真的可信度要求也日益增高,这使导弹仿真的可信度研究成为导弹仿真工作中的一个热点问题。Hermann[3]提出可以从不同的角度对仿真模型进行一致性验证;张津源[4]基于小子样理论的仿真模型一致性验证,主要用于处理静态数据的一致性验证;唐雪梅等[5]提出了基于TIC的非随机动态数据一致性检验;赵希尧[6]提出一种基于动静态性能的一致性分析的仿真模型验证方法,得出了很好的一致性结论。

本文以某新型中远距空空导弹仿真模型为研究对象,在该导弹模型仿真数据的基础上,结合外场试验数据提出了基于最大熵谱估计(Maximum Entropy Spectrum Estimation,MESE)的导弹仿真随机动态数据一致性验证方法,并取得了显著的效果。

1 试验数据的采集

1.1 数据需求分析

1.1.1 一致性验证的数据需求

导弹模型包括导弹制导模型、目标相对运动模型和脱靶量计算模型3部分[7]。目标相对运动模型输出导弹与目标的相对俯仰角和相对偏航角;导弹制导模型依据目标相对运动模型的输出量形成控制指令(俯仰指令和偏航指令)控制导弹的运动;导弹脱靶量计算模型主要用于导弹的脱靶量计算。因此,本文进行导弹仿真数据一致性验证时所涉及的仿真数据包括:导弹的脱靶量、俯仰角、偏航角、俯仰指令、偏航指令以及导弹与目标的相对俯仰角和相对偏航角。在进行外场试验时,需要对以上数据进行采集和记录,作为导弹仿真数据一致性验证的参考数据。

1.1.2 仿真试验的数据需求

对导弹进行仿真试验,其实质是用仿真模型代替真实系统进行动态试验;因此,必须以真实参数作为仿真试验的输入参数,主要包括:

(1)导弹参数:导弹的结构参数、推力、初始质量、最大及最小飞行速度、控制飞行时间、发动机工作时间、比例导引系数及作用距离等;

(2)目标参数:飞机与导弹的初始相对位置、速度、加速度、俯仰角、偏航角及外场试验中的运动规律等。

1.2 外场试验数据的采集

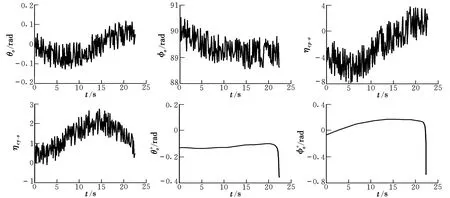
图1 外场试验数据Fig.1 Field test datas

1.3 导弹仿真参数设定

1.3.1 导弹参数

某型导弹的典型参数为:导弹翼面积0.3 m2;推力2 000 N，阻力系数0.12,最小和最大飞行速度为190 m/s和1 020 m/s;初始质量196 kg;发动机工作时间8 s;导弹供电时间65 s,引信作用距离400 m,最大过载26,比例导引系数3.5,导弹控制飞行时间50 s,引信接触保险时间0.8 s。

在地理坐标系[7]下,导弹发射位置为(1 000,0,4 000) m,初始运动速度为260 m/s,俯仰角为0°,偏航角为90°。

1.3.2 目标运动规则

目标作匀速运动,速度为280 m/s;航迹俯仰角变化率为1.3 (°)/s;航迹偏航角变化率为1.6 (°)/s。导弹发射时刻,目标的位置为(0,15 000,2 000)m,航迹俯仰角和航迹偏航角均为0°。

1.3.3 空气密度

空气密度可通过关于高度H的拟合函数求出:

ρ=2.280×10-10H2-1.028×10-5H+0.124

(1)

1.4 导弹仿真结果

在导弹仿真模型[7]的基础上,模拟外场真实的试验场景,构建全体系实战对抗仿真试验,并对仿真试验中的导弹仿真数据进行采集。第1次导弹仿真试验动态数据如图2所示。

进行10次导弹仿真试验,所产生的脱靶量R#分别为:

4.996 2 m,9.616 7 m,8.838 2 m,8.843 7 m,7.616 6 m,7.067 7 m,10.452 4 m,7.979 4 m,5.605 4 m,8.392 9 m。

图2 第1次导弹仿真试验动态数据Fig.2 Dynamic datas of the first missile simulation test

2 导弹仿真随机动态数据平稳化预处理

仿真试验产生的数据是不能直接用来开展一致性验证工作的,必须经过数据预处理,使数据的特征能够满足不同的验证方法。静态数据要剔除其中的奇异值,而动态数据要依据所选取的一致性验证方法进行时序一致性处理和平稳化处理。

对于随机动态数据x1,x2…,xn,在求取最大熵功率谱时,要求随机信号是平稳的,因此需要对随机的动态数据进行平稳化处理。对随机数据进行平稳化处理的一般方法为:先对其进行零均值化处理,再进行差分处理[8]。

零均值化处理就是将均值不为零的非平稳随机动态数据中的每个数据都减去该组数据的均值,构成一组新的随机动态数据,即:

(2)

(3)

经平稳化处理之后导弹仿真非随机动态数据包括导弹姿态角(俯仰角和偏航角)、俯仰指令、偏航指令。其数据的采样频率为10,平稳化处理之后的数据长度为223。

3 基于MESE的导弹仿真数据一致性验证

3.1 MESE在一致性验证中的应用

运用MESE[9]对动态数据进行验证,包括最大熵功率谱计算和一致性验证两个过程。

3.1.1 MESE

采用MESE进行功率谱的计算式为:

(4)

式中:σ2为模型中的白噪声功率;a(k) (1≤k≤p)为自回归序列的系数;p为模型阶次。

σ2和a(k)满足Yule-Walker方程:

(5)

式中:r(0),r(1),…,r(p)为自相关函数序列。

求取σ2和ak是最大熵功率谱计算的关键,其求解方法有很多,如Yule-Walker法、Marple法和Burg法等[10]。在此,应用Burg法来计算。

对于离散数列X={x(1),x(2),…,x(n)},取ρf和ρb分别表示前、后向预测误差功率。这时有:

(6)

式中:ef(i)和eb(i)分别为前、后向预测误差。当模型阶次为p时,有以下递推关系:

(7)

其中:

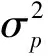
(8)

利用MESE进行功率谱计算时,估计阶次p的选取也是一项重要工作。目前,最优阶次的确定方法主要有:信息论准则、自回归传递函数准则以及最终预测误差准则[11]。当信噪比较大时,上述3种方法所确定的最优阶次没有太大的差异;但是,当信噪比较小时,依据最终预测误差准则确定的最优阶次相对于另外两种准则给出的结果要准确得多。因此,本文选取最终预测误差准则来确定最优阶次。最终预测误差准则为:

(9)

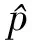
3.1.2 基于MESE的动态数据一致性验证

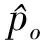
(10)

对于频率点ωj,若满足式(11),则认为So(ωj)和Si(ωj)一致,即仿真数据与参考数据是一致的。

(11)

3.2 导弹仿真数据一致性验证

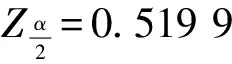
对第一次仿真试验产生的导弹俯仰角数据,先求其参考数据θo和仿真数据θ1的最大熵功率谱,结果如图3所示。

图3 导弹俯仰角的最大熵功率谱Fig.3 Maximum entropy spectrum of the missile pitch angle

在对导弹俯仰角θo和θ1求取最大熵功率谱时,AR模型最优阶次分别为8和9,则有:

对于第一次仿真试验输出的导弹俯仰角θ1,在最大熵功率谱中选取112个点进行检验,满足一致性要求的个数Mθ为96。

进行10次仿真试验,对于输出的导弹俯仰角,先采用阶次为9的AR模型计算出其最大熵功率谱;然后,均选取112个点进行一致性验证,满足一致性要求的频率点个数Mθ依次为:96,90,92,91,92,95,94,95,90,94。

经对仿真试验数据的分析可得达到一致性要求的点数与外场试验要求相差不大,置信度在90%以上,在可接受范围情况内。

同理,对导弹偏航角、俯仰指令、偏航指令在最大熵功率谱中各选取112个点进行检验,10次仿真试验均选取112个频率点进行一致性验证,其结果分别为:

(1)导弹偏航角φ1满足一致性要求的个数Mφ为91。每次仿真试验输出的导弹偏航角φi的验证结果Mφ依次为:91,95,96,93,92,86,95，94,94,93。

(2)导弹俯仰指令ncp-o(t)共有Mncp=103个频率点满足一致性要求。每次仿真试验验证结果Mncp依次为:103,96,97,98,92,94,93,96,96,90。

(3)导弹偏航指令共有Mncy=103个频率点满足一致性要求。每次仿真试验验证结果Mncy依次为:99,95,96,93,92,94,87,91,92,92。

通过以上基于MESE对导弹俯仰角、偏航角、俯仰指令和偏航指令的一致性验证,得到满足一致性要求的点数符合实际,偏差在10%左右,表明该方法合理、可行,导弹模型具有良好的动态一致性。

4 结束语

数据一致性验证分析对模型的可信性研究起到重要作用。本文提出基于MESE的仿真数据的一致性检验方法,通过对数据进行平稳化处理可有效解决随机输入信号的平稳化问题,完成对仿真结果的动态一致性定量检验,均得到较高的置信度,输出结果与实际情况相差不大,具有良好的可信性。下一步可通过建立更符合空战实际的作战模型,开展更详细的模型验证工作。

[1] 樊会涛.空空导弹方案设计原理[M].北京:航空工业出版社,2013:55.

[2] 焦鹏.制导仿真系统VV&A理论、方法和软件工具研究[D].长沙:国防科学技术大学,2004.

[3] Hermann C F.Validation problems in games and simulation with special reference to model of international politics[J].Behavioral Science,1967(3):216-231.

[4] 张津源.基于数据一致性分析的仿真模型验证方法及工具研究[D].哈尔滨:哈尔滨工业大学,2011.

[5] 唐雪梅,李荣,胡正东,等.武器装备综合试验与评估[M].北京:国防工业出版社,2013:46-48.

[6] 赵希尧.基于静动态性能一致性分析的仿真模型验证方法研究[D].哈尔滨:哈尔滨工业大学,2012.

[7] 李飞.战斗机末端规避决策与控制技术研究[D].西安:空军工程大学,2015.

[8] Oppenheim A V,Willsky A S,Hamid S.Signals and systems [M].New York:Prentice Hall,1996:181.

[9] 王建华,符文星,董敏周,等.最大熵谱估计在空空导弹仿真模型验证中的应用[J].弹箭与制导学报,2005,25(4):848-850.

[10] 吴方.时频域分析方法在仿真模型验证中的应用研究[D].哈尔滨:哈尔滨工业大学,2013.

[11] 戚宗锋,李林,刘文钊.电子信息系统仿真可信性评估方法[M].北京:国防工业出版社,2013:72-73.

(编辑：李怡)

Consistency validation of missile simulation data based on maximum entropy spectrum estimation

ZHAO Bin, ZHOU Zhong-liang, WANG Jin-fu

(Aeronautics and Astronautics Engineering College, AFEU, Xi’an 710038, China)

Simulation credibility evaluation method for air-to-air missile mode was studied, and the consistency validation method of missile simulation data based on maximum entropy spectrum estimation was proposed. The simulation test of the whole system was carried out on the simulated field test， and the data was used as the reference for the consistency of the simulation data. After smooth processing of the random dynamic data from missile simulation test, the consistency validation of the missile simulation random dynamic data was conducted on the basis of the maximum entropy spectrum estimation. Results show that the model has good dynamic consistency, and the validity and feasibility of the method are verified.

missile simulation; stabilization; maximum entropy spectrum estimation; consistency validation

2016-05-16;

2016-07-25;

时间:2016-09-13 11:07

赵彬(1992-)，男，山东济南人，硕士研究生，研究方向为武器总体技术与作战运用、作战效能评估。

TJ762.2

A

1002-0853(2016)06-0058-05