直升机机身气动外形的低阻优化设计

李杰, 徐明, 李建波

(1.中国直升机设计研究所 总体气动室, 江西 景德镇 333001;2.南京航空航天大学 直升机旋翼动力学国家重点实验室, 江苏 南京 210016)



直升机机身气动外形的低阻优化设计

李杰1, 徐明2, 李建波2

(1.中国直升机设计研究所 总体气动室, 江西 景德镇 333001;2.南京航空航天大学 直升机旋翼动力学国家重点实验室, 江苏 南京 210016)

直升机机身阻力是飞行阻力的主要来源之一,通过对机身外形的优化设计,能够实现直升机的高效低阻飞行。首先,把机身划分为头部、中段和尾梁三段,对其外形轮廓线进行CST参数化表示;其次,采用拉丁超立方法选取试验设计样本点,计算各样本点的阻力系数,构造Kriging代理模型,估计模型预测的精度;最后,选用序列二次规划算法对其进行优化,并对优化后的机身模型进行了风洞试验。通过计算分析可知:所建立的Kriging代理模型能够精确预测阻力系数值,优化后得到了机身的设计参数;机身阻力系数减小了15.3%,理论值与试验值吻合良好。

直升机机身; 气动外形; CST方法; 优化设计

0 引言

降低直升机机身阻力已成为直升机设计的一项重要工作。在早期的直升机机身外形设计中,由于理论分析手段尚未成熟,主要通过风洞试验来研究直升机机身的气动特性,根据经验来设计低阻的直升机机身外形。目前,国内外通常采用CFD预估和直升机机身模型的风洞试验来研究机身减阻问题。但是,CFD预估得到的机身外形不一定最优,风洞试验也存在周期长、代价高的缺点。

外形参数化方法的选取对气动外形设计影响较大,所采用的参数化方法既要确保最优解在设计空间中,又要用较少的参数来定义高精度的几何形状,从而降低优化设计过程中的计算量。目前,外形参数化方法有B样条曲线法、Hicks-Henne法、PARSEC法和CST(Class Shape Transformation)参数化方法[1-5]等。其中,CST参数化方法的运算效率高、数值稳定、精确度高。通过CST方法对外形进行参数化分解时,能够使用较少的参数来定义较大的设计空间,灵活方便地设计和修改外形。

本文采用CST参数化方法对某型直升机机身外形进行了参数化建模,构造了机身阻力系数的Kriging代理模型,并结合总体设计方案中机身布置的要求,采用序列二次规划算法对机身的气动外形进行低阻优化设计。为了验证理论计算的准确性,在南京航空航天大学的非定常、低噪声、低湍流风洞中进行了直升机机身模型的吹风试验。

1 直升机机身外形的CST参数化表示

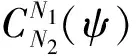
若模型尾部外形封闭,则:

(1)

式中:ψ=x/c,ζ=y/c(其中x,y分别为模型在x轴、y轴中的坐标,c为模型长度);N1和N2代表了几何外形的类别。

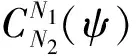
(2)

若模型尾部外形不封闭,则:

(3)

式中:Δζ为模型尾部厚度参数。

采用n阶Bernstein多项式的加权和当作S(ψ)的定义式:

(4)

(5)

式中:bi(i=0,1,…,n)为权重因子,构成几何形状的n+1阶参数向量b。b=[b0,b1,…,bn],能够通过以下矩阵方程求出:

[b0,b1,…,bn]=[ζ(ψ0),ζ(ψ1),…,ζ(ψn)]A

(6)

其中:

(7)

使用3阶与10阶之间的Bernstein多项式能保证参数化过程数学形态良好。

直升机机身的外形主要取决于其纵向轮廓线和特征横截面的形状。设计机身的气动外形时,需要对其进行CST参数化建模。由于A160机身表面平滑过渡,整体比较修长,流线型较好,所以本文参考A160机身给出初始的模型机身。根据直升机机身的功用和结构特点,将机身分为三部分,分别为头部、中段和尾梁,如图1所示。将机身特征横截面分为上、下两部分,如图2所示。图1中的L为模型机身的长度,图2中的w为特征横截面的宽度。

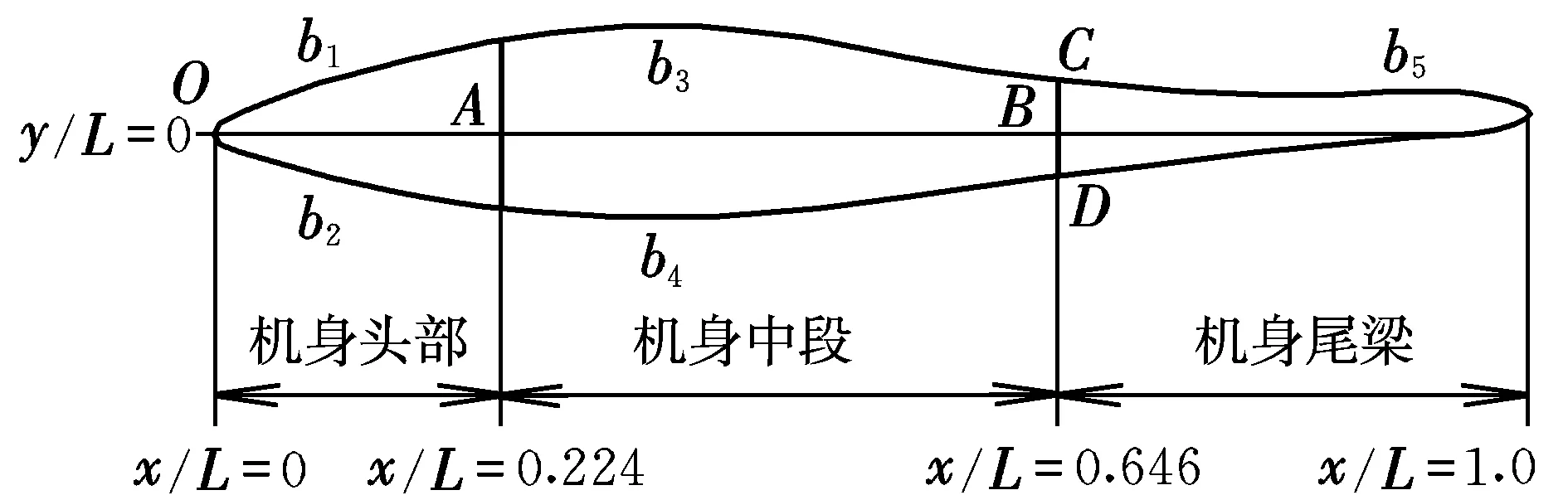
图1 模型机身纵向轮廓线Fig.1 Longitudinal profile of model fuselage

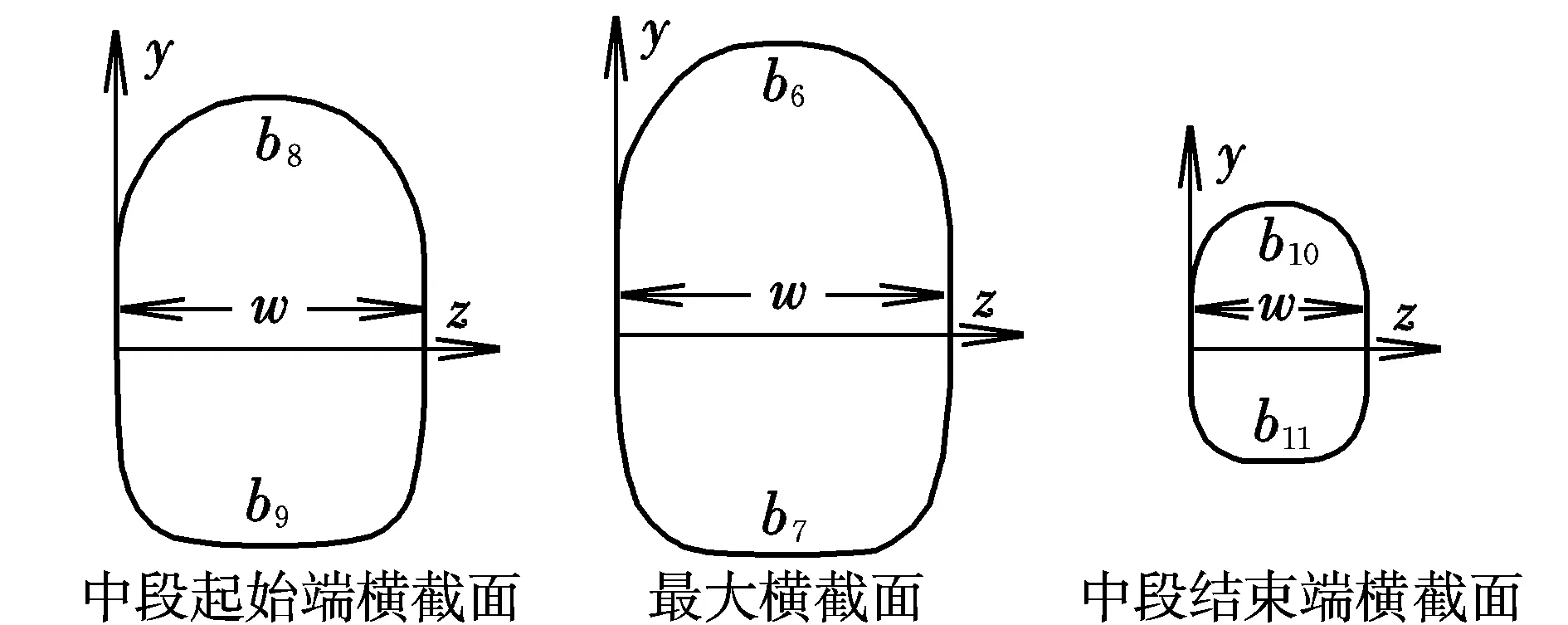
图2 模型机身特征横截面Fig.2 Characteristic cross section of model fuselage

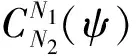
2 低阻优化设计

2.1 试验设计方法及样本点的选取

试验设计方法影响着创建代理模型所需样本点的个数和其空间分布。本文采用基于迭代局部搜索算法的带有极大极小准则的中心拉丁超立方法[6-7]获得样本点。由于直升机头部的外形对其前飞阻力系数有着重要的影响,所以对其头部外形进行优化设计。机身头部顶、底端线的参数分别为(b1-0,b1-1,b1-2),(b2-0,b2-1,b2-2),代表了机身头部外形的曲面弧度和上下对称性的特征,其变化范围如表1所示,分别在6个参数的范围内选取了70个样本点。

表1 设计参数的范围

Table 1 Scope of design parameters

参数值b1-0b1-1b1-2b2-0b2-1b2-2最小值0-015-0270010028最大值0160-026016025029

2.2 代理模型的构造

代理模型能够过滤掉原分析模型可能出现的计算数值噪声,解决工程优化中计算量过大的问题,缩减优化设计的周期。Kriging模型[8-9]是一类估计方差最小的无偏估计模型,其系统的自变量和响应值之间的关系如下:

f(x)=g(x)+z(x)

(8)

式中:g(x)是一个确定性部分,称为确定性漂移;z(x)是对模拟部分偏差的近似,称为涨落。

Kriging模型拥有部分估计的特征。为了可以创建比较精准的Kriging代理模型,样本点的个数通常选取输入参数个数的10倍以上。Kriging代理模型可以使用许多均匀分布的样本点拟合十分复杂的外形。

本文采用CFD方法对直升机机身气动力系数进行计算,选用N-S方程作为主控方程,S-A单方程模型作为湍流模型。分别计算70个样本点在机身巡航速度为234 km/h状态下的机身阻力系数,从而构造Kriging代理模型,创建数据文件。

在构造Kriging代理模型后,需要对其拟合的精度进行检验。通过分析代理模型预测值与计算值之间的最大绝对误差(MAE)和均方根误差(RMSE),从而评价模型精度。如果最大绝对误差和均方根误差都小于10-4,则认为模型满足精度要求。

2.3 优化算法的选取

本文采用序列二次规划法作为优算法化,该方法能够较好地解决中、小规模的非线性规划问题。为了获取待解问题的最优解,需把待解问题转变为二次规划子问题求解,同时对拉格朗日函数选择二次近似,以提高二次规划子问题的相似程度。本文优化设计的整体流程如图3 所示。

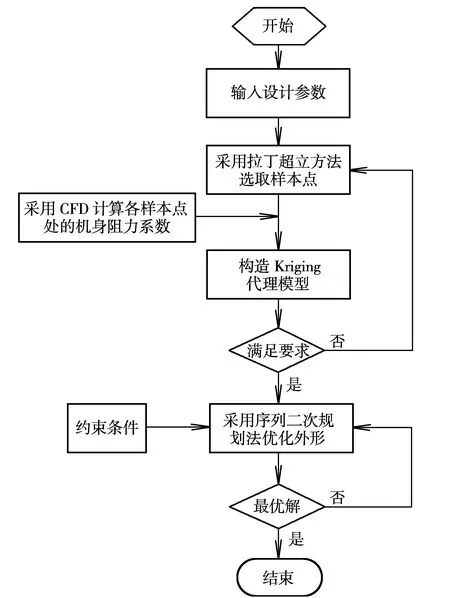
图3 优化设计流程示意图Fig.3 Schematic diagram of optimization design process

3 优化算例及分析

3.1 优化问题的表述

在本文优化算例中,综合考虑直升机机身总体设计方案要求,在机身中段内部主要布置旋翼减速器、发动机、操纵系统和燃油箱,在机身尾梁安装尾桨,进而给出机身中段和尾梁的尺寸约束。具体优化问题的详细表述如下:

(1)给定参数:机身中段顶、底端线的参数b3和b4;机身尾梁纵向轮廓线的参数b5;

(2)目标函数:在巡航状态下,巡航速度为234 km/h时的阻力系数CD最小;

(3)设计参数:机身头部顶、底端线的参数(b1-0,b1-1,b1-2)和(b2-0,b2-1,b2-2);

(4)约束条件:机身特征横截面的向量参数值b6≥b6min,b7≥b7min,b8≥b8min,b9≥b9min,b10≥b10min,b11≥b11min。

3.2 结果分析

按照上述优化设计方法和流程,对算例机身进行优化设计。经过52步迭代后,机身阻力系数的迭代监控曲线逐渐收敛,如图4所示。可以看出,优化后的机身阻力系数为0.061 1,比原始机身模型减小了15.3%。

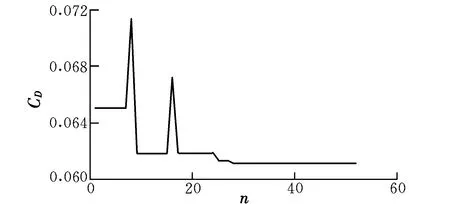
图4 优化过程中机身阻力系数的迭代监控曲线Fig.4 Iteration monitoring curve of fuselage drag coefficient in optimization process

Kriging模型检验的最大绝对误差和均方根误差分别为8.3×10-5和2.4×10-5,均小于10-4,满足精度要求。将优化后的设计参数与优化前的设计参数进行对比,结果如表2所示。

表2 优化参数比较

Table 2 Comparison of optimized parameters

状态b1-0b1-1b1-2b2-0b2-1b2-2优化前00029-015-0267003240119802843优化后005860-0265000850217302832

通过计算分析,得到阻力系数随设计参数变化的趋势,对比讨论各个设计参数对计算结果的影响,如图5所示。可以看出:在设计空间内,随着b1-0的增大,机身阻力系数CD先减小后增大;参数b1-1越大,CD就越小;随着参数b1-2,b2-0,b2-1,b2-2的增大,CD先减小后增大。

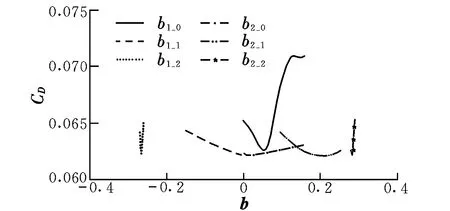
图5 机身阻力系数与优化后设计参数的关系Fig.5 Relationships between fuselage drag coefficient and optimized design parameters

根据以上计算结果以及得到的结论,获得优化后机身的气动外形如图6所示。可以看到,优化后机身头部在纵向截面上趋于对称,采用了较小的圆弧形式过渡。

图7为优化前后的机身在巡航状态下沿顶、底端线的压力系数分布。可以看出:优化前的机身沿顶端线的负压最大值位置在x=3.5 m处,最大负压系数约为-0.198;优化后的机身沿顶端线的最大负压系数减小至-0.1,并且峰值的位置有所前移,导致静压较大的区域进一步缩小;在机身头部以及中段附近区域,压差逐渐减小,使得阻力方向的分量减小,进而阻力系数呈现减小的趋势。

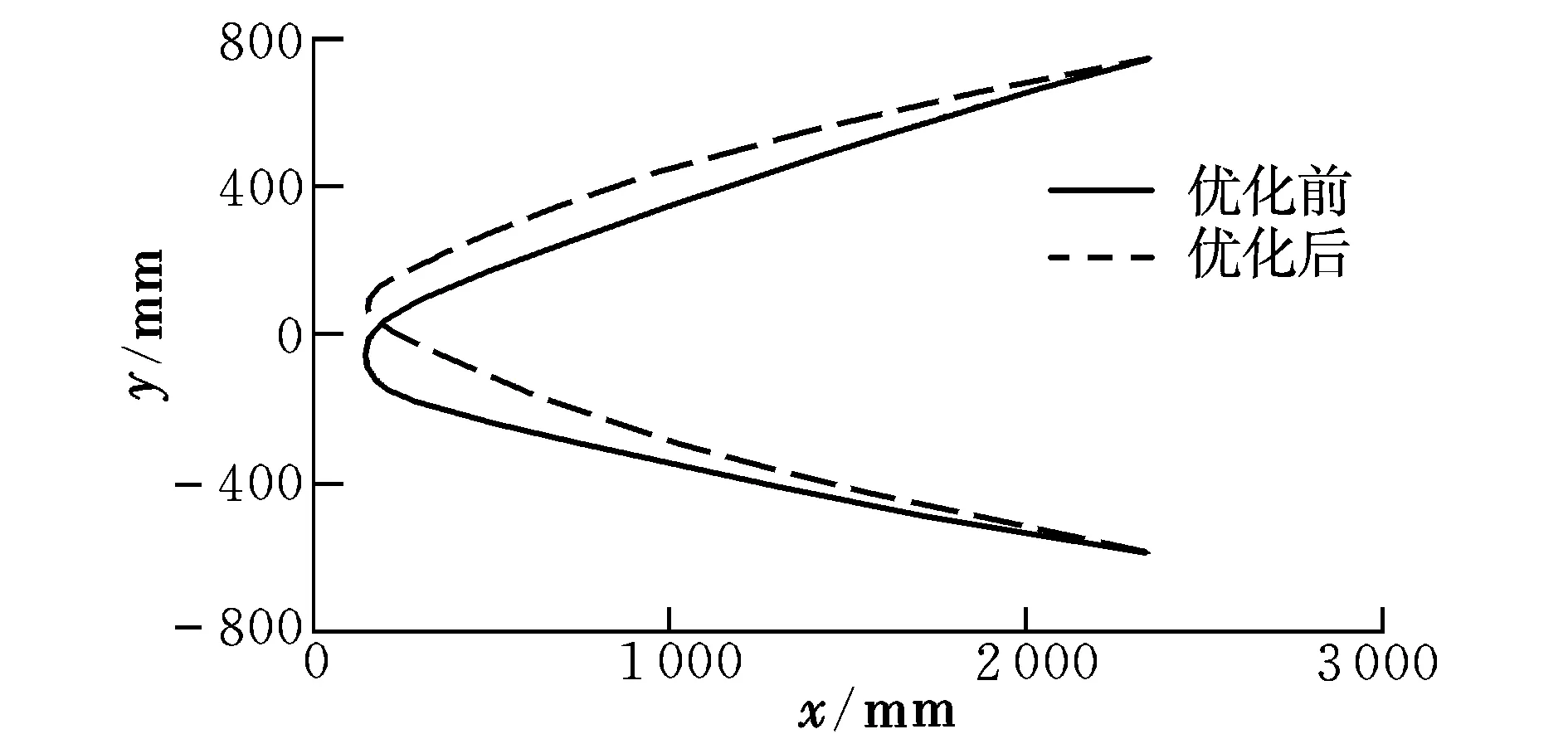
图6 优化前后机身头部纵向轮廓线的对比Fig.6 Comparison of fuselage head longitudinal profiles between initial and optimized shape

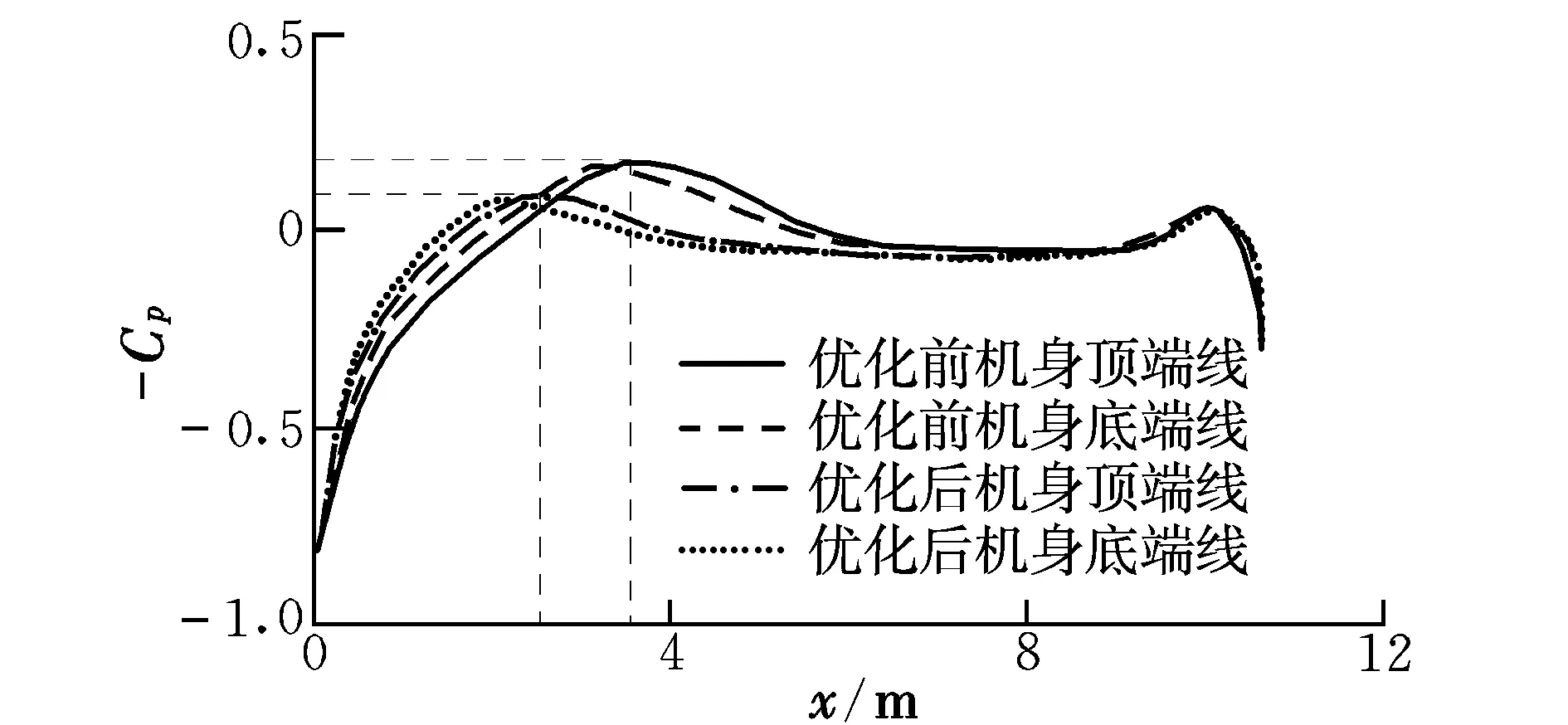
图7 优化前后机身沿顶、底端线压力系数分布的比较Fig.7 Comparison of pressure coefficient distribution for top and bottom lines between initial and optimized fuselages

3.3 计算值与试验值的对比

设计并制作机身模型、杆式天平整流罩模型以及一些连接件。按照风洞试验要求[10]安装试验模型如图8所示。在进行正式的机身模型试验测量前,需要对试验设备及试验模型进行检查和调试,同时进行重复性试验,最大限度地减小试验误差。

图8 试验模型连接示意图Fig.8 Connection diagram of test model

机身模型的升力系数和俯仰力矩系数对配平结果、机身姿态以及阻力系数有影响,所以本文将巡航状态下的机身模型阻力系数CD、升力系数CL和俯仰力矩系数Cm与相应的试验结果进行了比较,结果如图9所示。

可以看出,机身模型阻力系数的计算值与试验值的最大差值为1.7%,升力系数和俯仰力矩系数的计算值与试验值的最大差值分别为2.3%和4.1%,说明理论计算的数值可靠性较高。

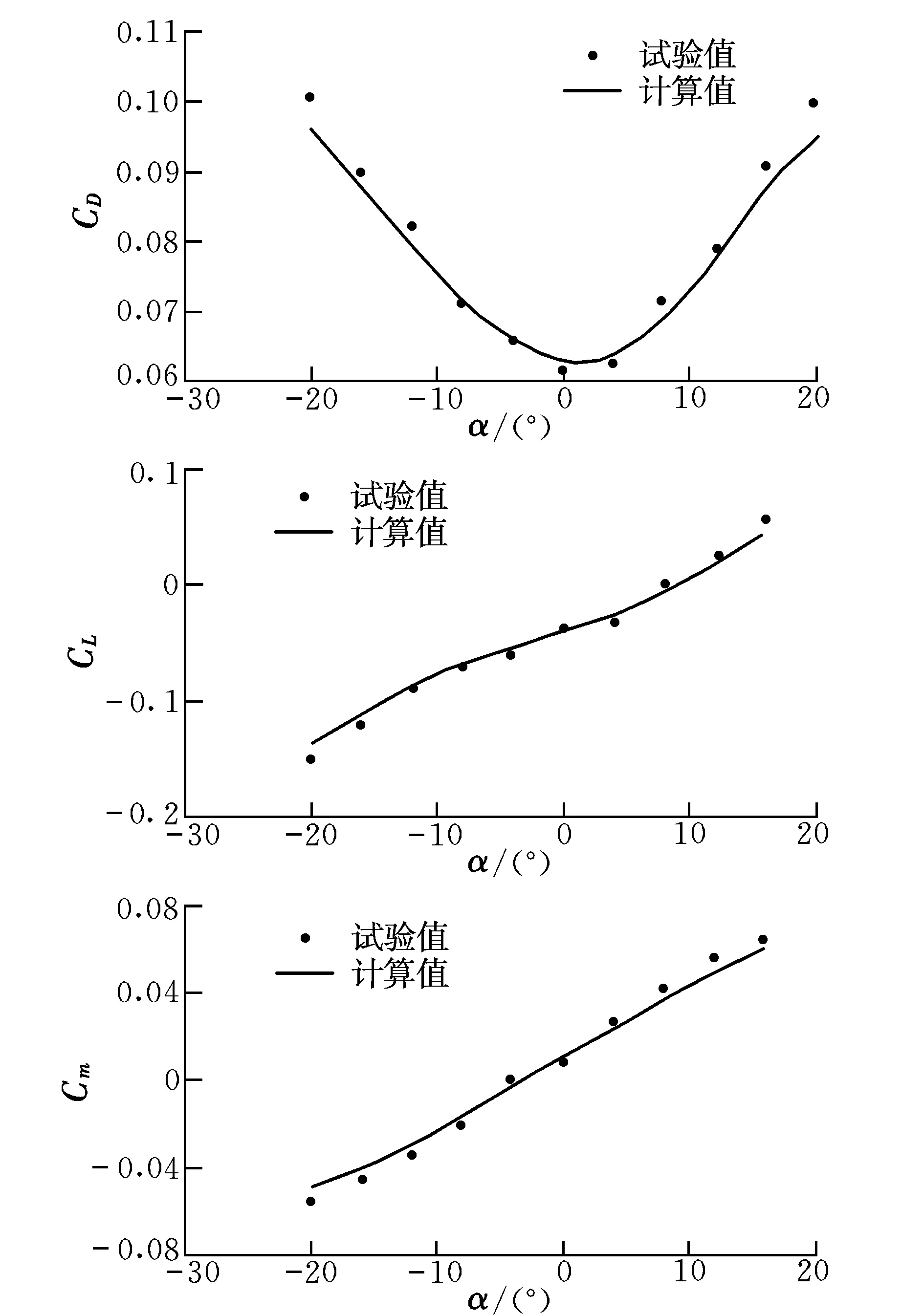
图9 计算值与试验值的对比Fig.9 Comparison of calculated values and tested values

4 结束语

采用CST参数化方法能够很好地表示直升机机身的气动外形,构造出精确的Kriging代理模型来

预测机身的阻力系数。本文采用的优化设计方法能够用于直升机机身气动外形的低阻优化设计,缩短了机身外形设计的周期,节约了成本,在工程实际中具有较大的应用价值。

[1] Sripavadkul V,Padulo M,Guennov M.A comparison of airfoil shape parameterization techniques for early design optimization[R].AIAA-2010-9050,2010.

[2] Ceze M,Hayashi M,Volpe E.A study of the CST parameterization characteristics[R].AIAA-2009-3767,2009.

[3] Brenda M K,Bussoletti J E.Fundamental parametric geometry representations for aircraft component shapes[R].AIAA-2006-6948,2006.

[4] Brenda M K.A universal parametric geometry representation method:CST [R].AIAA-2007-62,2007.

[5] 张磊,陈红全.基于CST参数化的翼型优化遗传算法研究[J].航空计算技术,2011,41(6):53-57.

[6] Roshan V J.Orthogonal-maximin Latin hypercube designs[J].Statistica Sinica,2008,18(1):171-186.

[7] Grosso A.Finding maximin Latin hypercube designs by iterated local search heuristics[J].European Journal of Operational Research,2009,197(2):541-547.

[8] Simpson T W,Mauery T W,Korte J,et al.Comparison of response surface and Kriging models for multidisciplinary design optimization[R].AIAA-98-4755,1998.

[9] 王晓锋,席光.基于Kriging模型的翼型气动性能优化设计[J].航空学报,2005,26(5):545-549.

[10] Vogel F,Breitsamter C,Adams N A.Aerodynamic investigations on a helicopter fuselage[R].AIAA-2011-3820,2011.

(编辑：崔立峰)

Low-drag optimization design of aerodynamic shape for helicopter fuselage

LI Jie1, XU Ming2, LI Jian-bo2

(1.General Configuration and Aerodynamics Department, Chinese Helicopter Research and Development Institute, Jingdezhen 333001, China; 2.National Key Laboratory of Rotorcraft Aeromechanics, NUAA,Nanjing 210016, China)

Helicopter fuselage drag was one of the flight drag source, high efficient and low drag flight of helicopter was realized through the optimization design of the fuselage shape. First, fuselage was divided into three sections: fuselage head, middle and tail beam, outline profile was parameterized by class shape transformation(CST).Secondly, the Latin hypercube method was used to select experimental design sample points, drag coefficients of sample points was calculated, Kriging agent model was built and precision of agent model prediction was estimated. Finally,the sequential quadratic programming algorithm was used for its optimization, and wind tunnel test was conducted for optimized fuselage model. Through calculation and analysis, Kriging agent model can accurately predict drag coefficient value, get the fuselage design parameters after optimization, and the fuselage drag coefficient decreases by 15.3%, theoretical values are consistent with experimental values.

helicopter fuselage; aerodynamic shape; CST method; optimization design

2015-11-04;

2015-12-27;

时间:2015-12-30 10:02

江苏省高校优势学科建设工程资助项目；江苏省普通高校研究生科研创新计划(CXLX13_164)

李杰(1989-)，男，江西九江人，工程师，硕士研究生，研究方向为直升机总体设计和直升机空气动力学。

V211.52

A

1002-0853(2016)06-0077-05