超低空空投航迹倾角自适应跟踪控制
吕茂隆, 孙秀霞, 刘树光, 刘棕成, 洪洋
(空军工程大学 航空航天工程学院, 陕西 西安 710038)
超低空空投航迹倾角自适应跟踪控制
吕茂隆, 孙秀霞, 刘树光, 刘棕成, 洪洋
(空军工程大学 航空航天工程学院, 陕西 西安 710038)
针对超低空空投下滑阶段考虑执行器输入死区、不确定性大气扰动以及模型存在未知非线性等因素干扰轨迹精确跟踪等问题,提出了一种自适应神经网络动态面跟踪控制方法。建立了含执行器输入死区的超低空空投载机纵向非线性模型,采用神经网络逼近模型中未知非线性函数,引入非线性鲁棒补偿项消除了执行器死区建模误差和外界扰动。应用Lyapunov稳定性理论证明了闭环系统所有信号均是有界收敛的。仿真验证表明,所提方法既保证了轨迹跟踪的精确性,又具有强鲁棒性。
超低空空投; 执行器死区; 神经网络; 自适应控制
0 引言
超低空空投是指运输机在距地3~10 m,借助牵引伞等减速装置将物资投放到指定区域的过程,包括准备、下滑、改平、牵引和拉起5个阶段,是提高现代化战争战斗力的必要手段[1-2]。
近年来,为实现运输机空投下滑轨迹的精确跟踪,保证空投精确性和载机安全性,国内外学者做了大量研究[1,3-4]。文献[1]结合输入/输出反馈线性化与滑模变结构控制方法设计了速度与姿态内环跟踪控制器,利用PID实现外环高度保持。文献[3]基于线性化处理后的模型动态分段,提出运用鲁棒控制方法实现载机飞行状态的稳定。文献[4]基于滑模控制方法,设计了一种能有效抑制外界动态扰动的双环滑模混合迭代控制器。遗憾的是,上述文献在设计控制器过程中均没有考虑执行器输入存在死区的情况,忽略了执行器的动态特性和非线性因素,认为舵面偏转角指令和实际偏转角相等[5]。而由于实际驱动操纵舵面偏转的舵机执行机构包含机械链接和液压传动装置,必然导致舵机中存在死区现象,且死区非线性环节不可避免地将减弱系统稳定性,甚至导致系统发散[6]。目前,考虑执行器输入存在死区设计载机控制律的文章还未见报道,但是对非线性系统死区的控制方法已进行了不少研究。文献[7]基于模糊控制的逼近能力,设计双Lyapunov函数证明了建模误差和跟踪误差的收敛性,有效克服了控制输入的颤振现象。文献[8]基于系统状态完全可测以及死区坡度已知的条件,针对不对称执行器死区提出一种自适应控制方案,该方法无需构造自适应逆,有效消除了死区对系统的不良影响。
针对执行器输入存在死区的空投下滑阶段航迹角跟踪控制问题,本文提出自适应神经网络控制。采用参数自适应律对执行器未知建模误差和外界扰动进行在线估计,引入鲁棒补偿项和神经网络实现闭环系统稳定控制,有效消除了执行器非线性对系统的影响,最后通过仿真验证了本文方法的有效性。
1 问题描述
1.1 含执行器输入死区的空投下滑阶段载机模型
空投下滑阶段,载机的横侧向运动状态几乎不发生变化,考虑执行器死区载机的纵向模型可表示为[4]:
(1)
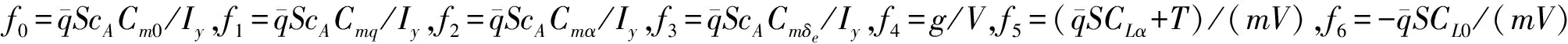
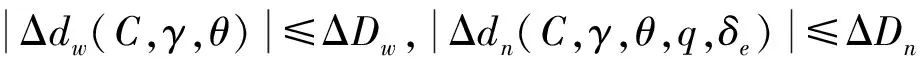
1.2 执行器死区建模
本文针对载机舵机执行器中实际存在的死区非线性环节,建立如下执行器非线性传动模型:
fδ(u)=k(u,t)u+εδ(u)
(2)
式中:k(u,t)>0为未知常数;εδ(u)为未知建模误差。

假设3: 模型(2)中的k(u,t)满足有界条件,即存在未知正数kmin和kmax使得:
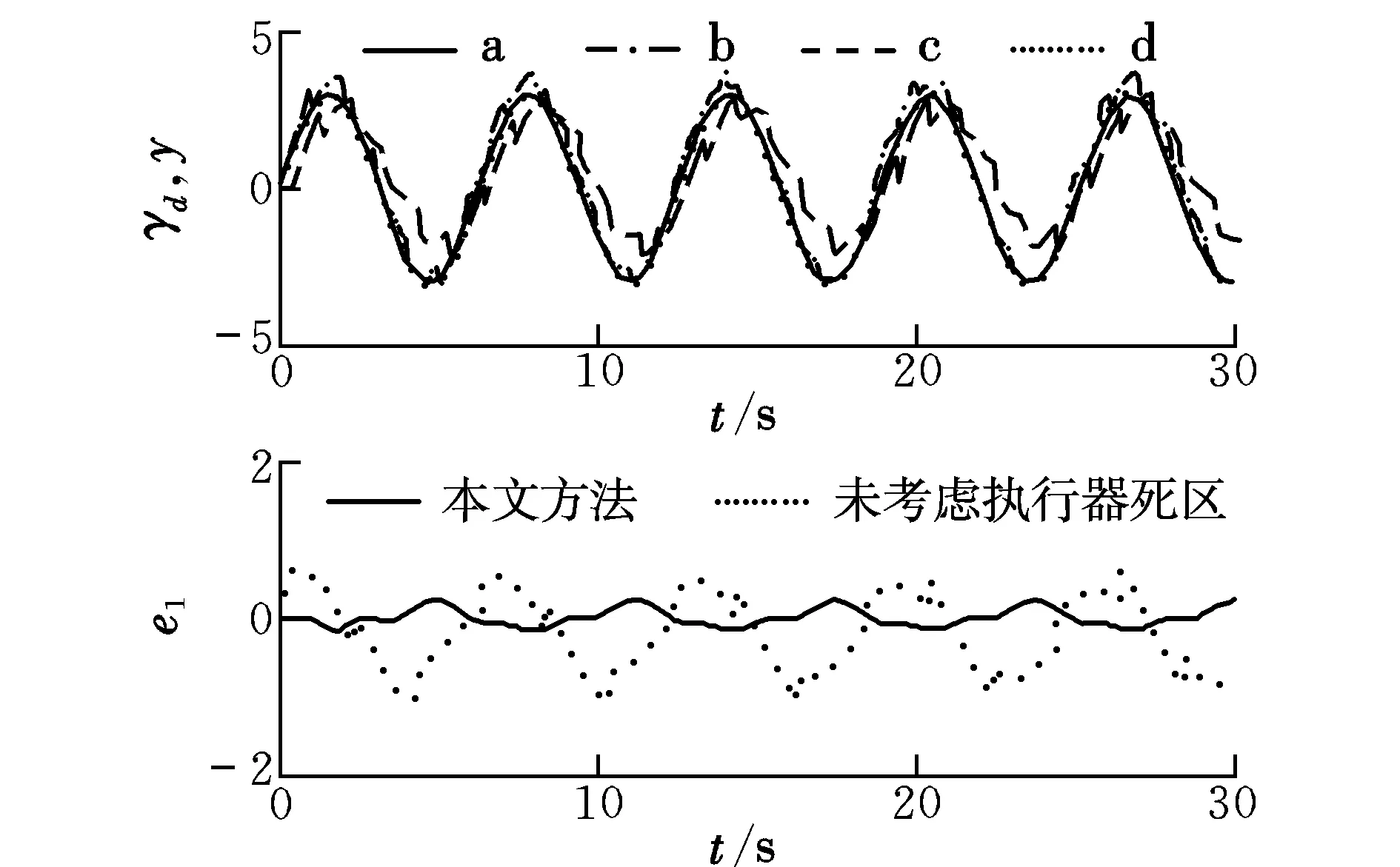
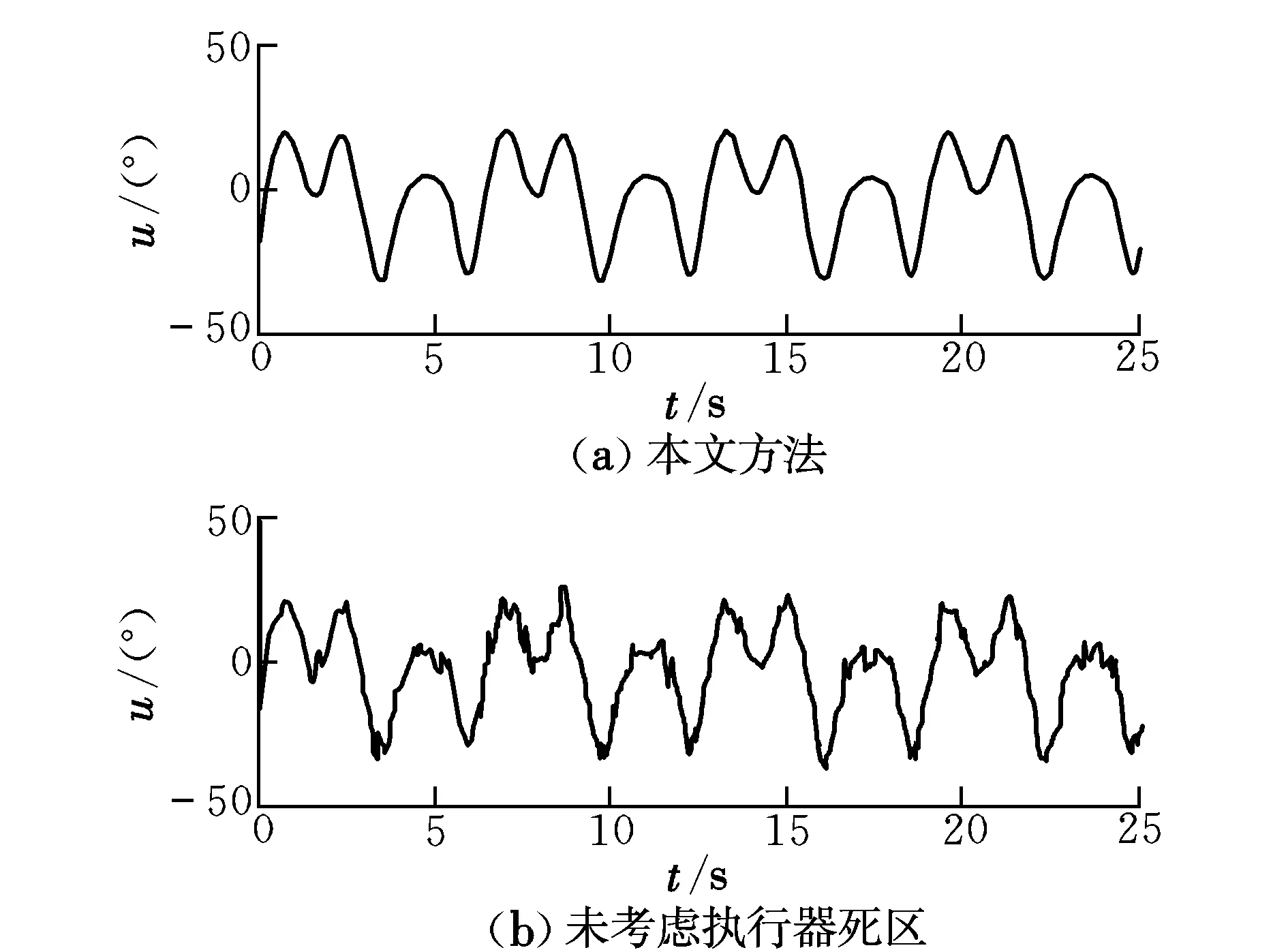
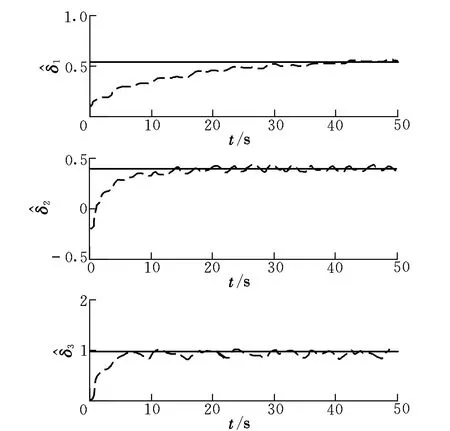
0 (3) 恒成立。 综上,执行器死区数学模型可描述为: (4) 式中:k(u,t)为死区坡度;bl>0和br>0分别为发生死区的起始点和终止点。令模型(2)中未知建模误差εδ(u)为: (5) (6) 控制目标为:载机纵向模型(1),设计控制器使载机下滑航迹倾角γ能够快速精确地跟踪参考指令γd。 为方便表达,定义变量[x1,x2,x3]T=[γ,θ,q]T,Δdw(·),Δdn(·),ΔDw(·)和ΔDn(·)分别用Δdw,Δdn,ΔDw和ΔDn表示,则模型(1)可写成如下形式: (7) 引理1[9]:若N(ζ)是Nussbaum函数,且下式成立: 引理 2[10]:双曲线正切函数tanh(·)连续且可导,并满足对任意q∈R 和ζ>0,有如下不等式成立: (8) 2.1 径向基神经网络 (9) 2.2 控制器设计 仿照反推“递进式”控制器设计方法,自适应神经网络飞行控制律设计步骤如下: 第1步:考虑第1阶子系统,定义第1个误差变量e1=x1-γd,并对e1求导: (10) 设计如下虚拟控制律和参数自适应律: (11) (12) 将α1输入到时间常数为τ2的低通滤波器,得到新的状态变量α2,f: (13) 第2步:定义第2个误差变量: e2=x2-α2,f (14) 设计第2步虚拟控制律和参数自适应律: (15) (16) 同理,将α2输入到时间常数为τ3的低通滤波器,得到新的状态变量α3,f: (17) 第3步:定义第3个误差变量e3=x3-α3,f,结合式(7)和式(9)对e3求导可得: (18) 最后,设计控制律和参数自适应律为: (19) (20) (21) 定理1:针对被控对象(7),对于式(11)、式(15)、式(19)和式(20)的控制律以及参数自适应律式(12)、式(16)和(21)组成的闭环系统,若假设1~4成立,且系统初始状态有界,则存在控制参数σi(i=1,2,…,6),ki,υi和τi(i=2,3)使闭环系统所有状态半全局一致,最终有界且跟踪误差可收敛至原点任意小邻域。 定义第3阶子系统的Lyapunov函数为: (22) (23) 将参数自适应律(21)带入式(23),并结合引理2可得: (24) 利用Young’s不等式化简式(24)可得: (25) 其中: 将式(25)两边同时乘以eβt,并对t积分可以得到: a0/β+V3(0) (26) 根据假设3且结合引理1,不妨设: (27) 由式(26)和式(27)可得: V3≤a0/β+V3(0)+Q (28) 由式(23)和式(28)可知V3(t)有界,且有: (29) 式中:Q>0,M>0为未知常数。 定义边界层误差: y2=α2,f-α1,y3=α3,f-α2 (30) 由式(10)~式(12)、式(14)~式(16)、式(18)~式(21)和式(30)可知,存在非负连续函数B2(·)和B3(·)满足: (31) 由上式可得如下不等式: (32) 同理,定义第1阶子系统Lyapunov函数为: (33) 注意到x2=e2+α1+y2,由Young’s不等式、引理2以及式(11)和式(12),对V1求导可得: (34) 定义第2阶系统Lyapunov函数为: (35) 结合引理2对V2求导有: (36) 考虑如下Lyapunov函数: V=V1+V2 (37) 结合式(32)、式(34)和式(36)对V求导可得: (38) (39) (40) 求解上式可得V≤a4/(2μ)+[V(0)-a4/(2μ)]×e-2ut,显然,闭环系统所有状态变量半全局一致最终有界,且有: (41) 为考察死区对空投控制性能的影响,将本文方法与未考虑执行器死区的自适应动态面控制方法进行对比,仿真结果如图1所示。仿真所用死区数学模型如下: (42) 图1 航迹角跟踪、跟踪误差曲线比较Fig.1 Comparison of flight path angle tracking and tracking error curves 首先,考察无外界干扰项Δdw和Δdn时,死区对系统控制性能的影响,采用未考虑死区的自适应动态面控制器,死区模型如式(42)所示,仿真结果如图1中曲线b所示,曲线a为期望航迹角指令曲线,对比a和b可知,死区的出现导致系统控制性能降低,载机无法精确跟踪期望航迹角指令。曲线d为本文方法对应的航迹倾角跟踪曲线。 再考察执行器存在死区的情况,同时增加外界大气干扰项Δdw和Δdn对载机控制性能的影响,仿真结果如图1中曲线c所示。此时载机的航迹角跟踪控制性能严重下降,极可能造成闭环系统不稳定,严重威胁空投的精确性与安全性。 控制输入和自适应参数对比仿真结果如图2和图3所示。图中,实线为参数真实值,虚线为自适应参数估计值。 图2 控制输入曲线比较Fig.2 Comparison of control input curves 图3 自适应参数估计值变化曲线Fig.3 Curves of adaptive parameter estimation 由图1可知,本文控制方法设计的飞控系统有效克服了载机执行器死区及外界大气干扰对系统的影响,保证了载机能迅速精确跟踪到航迹角参考指令,且跟踪误差迅速趋近于0。未考虑执行器死区的方法相比于本文方法,跟踪误差明显增加。 由图2可知,本文方法有效克服了由死区引起的控制输入颤振现象。由图3可知,自适应未知参数的估计值逐渐逼近实际值,且具有较好的逼近效果。 本文针对执行器死区、模型函数未知和外部大气扰动的载机纵向模型,提出了一种自适应神经网络动态面控制方法。该方法有如下优点:(1)有效克服了死区非线性对系统造成的不良影响;(2)准确估计了模型未知参数,采用神经网络逼近模型未知系统函数,取消了模型函数必须已知的假设;(3)引入了鲁棒自适应补偿项,有效消除了外界大气扰动、神经网络逼近误差和死区建模误差对系统造成的不良影响;(4)对于解决类似结构的一类含执行器死区的不确定严反馈非线性系统的跟踪控制问题具有一定的参考价值。 [1] Zhang H Y,Shi Z K.Variable structure control of catastrophic course in airdrop heavy cargo[J].Chinese Journal of Aeronautics,2009,22(5):521-525. [2] 吕茂隆,孙秀霞,王栋.运输机超低空空投下滑阶段PIO趋势评估与抑制[J].飞行力学,2016,34(1):26-30. [3] Feng Y,Shi Z K,Tang W.Dynamics modeling and control of large transport aircraft in heavy cargo extraction[J].Journal of Control Theory and Application,2011,9(2):231-236. [4] 刘日,孙秀霞,董文瀚.超低空空投拉平阶段混合迭代滑模控制[J].北京航空航天大学学报,2015,41(1):83-89. [5] Harkegard O,Torkel G S.Resolving actuator redundancy-optimal control vs control allocation[J].Automatica,2005,41(1):137-144. [6] 李恒,张友安,孙富春.多操纵面飞机全局集合稳定非线性自适应动态控制分配[J].控制与决策,2013,28(3):379-390. [7] 王芹,张天平,文慧.具有非线性输入的鲁棒自适应模糊滑模控制[J].电机与控制学报,2008,12(1):52-57. [8] Ibrir S,Xie W F,Su C Y.Adaptive tracking of nonlinear systems with non-symmetric dead-zone input[J].Automatica,2007,43(3):522-530. [9] Ge S S,Hong F,Lee T H.Adaptive neural control of nonlinear time-delay system with unknown virtual control coefficients[J].IEEE Transactions on Systems,Man and Cybernetics,2004,34(1):499-516. [10] Wen Y,Ren X.Neural networks-based adaptive control for nonlinear time-varying delays systems with unknown control direction[J].IEEE Transactions on Neural Networks,2011,22(10):1599-1611. (编辑:方春玲) An adaptive tracking controller for ultra-low altitude airdrop flight path angle LYU Mao-long, SUN Xiu-xia, LIU Shu-guang, LIU Zong-cheng, HONG Yang (Aeronautics and Astronautics Engineering College, AFEU, Xi’an 710038, China) For the ultra-low altitude airdrop decline stage, many factors such as actuator dead-zone, the uncertain atmospheric disturbances and model unknown nonlinearity affect the precision of trajectory tracking, an adaptive neural network dynamic surface control scheme is proposed. The ultra-low altitude airdrop longitudinal dynamics with actuator dead-zone is established, the neural network is used to approximate unknown nonlinear functions of the model and a nonlinear robust term is introduced to eliminate the actuator’s nonlinear modeling error and external disturbances. From Lyapunov stability theorem, it is proved that all the signals in the close-loop system are bounded. Simulation results confirm the perfect tracking performance and strong robustness of the proposed method. ultra-low altitude airdrop; actuator dead-zone; neural network; adaptive control 2016-03-22; 2016-08-15; 时间:2016-09-22 14:55 航空科学基金资助(20135896025,20155896025);博士后科学基金资助(2014M562629) 吕茂隆(1991-),男,四川绵阳人,硕士,研究方向为飞机飞行品质; 孙秀霞(1962-),女,山东潍坊人,教授,博士生导师,研究方向为现代鲁棒控制和飞行控制。 V249.1 A 1002-0853(2016)06-0039-06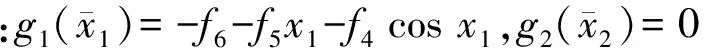
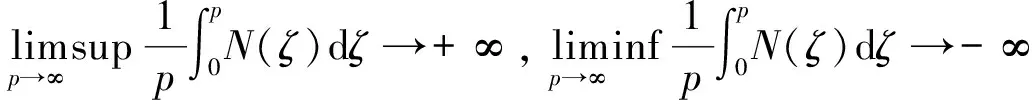
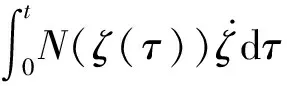
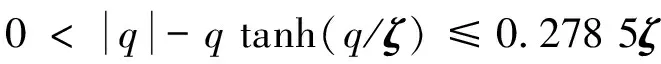
2 自适应神经网络控制律设计
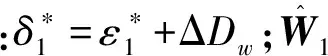
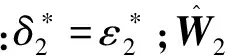
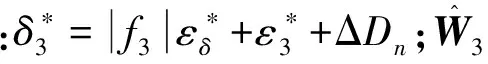
3 稳定性证明及跟踪性能分析
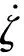
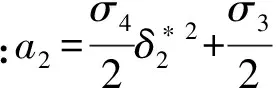
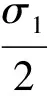
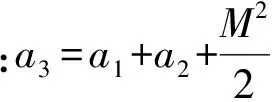
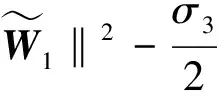

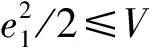
4 仿真验证
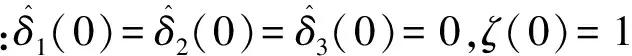
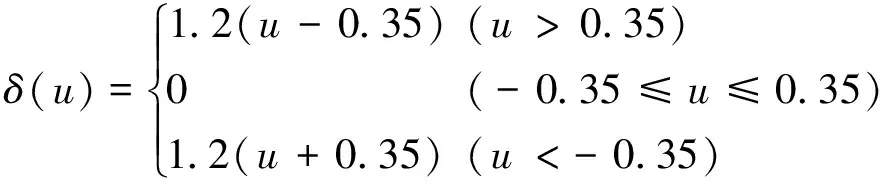
5 结束语

