无筒空射运载火箭重力出舱机箭耦合动力学

韩艳铧，尹文博，张 勇

（1.南京航空航天大学航天学院，南京 211106；2.南京航空航天大学无人机研究院，南京 210016）

空射运载火箭在商用、军事等领域用途广泛［1⁃2］。按照火箭装载方式分为下挂、背驮、内装、拖曳4 种［3⁃4］。相比于陆基发射，空射具有多方面的优点［5⁃8］。

内装式空射将火箭固定在机舱内，载机到达预定空域和飞行状态后解锁火箭，机⁃箭分离后点火发射［9⁃10］。箭头与机头方向一致为前向发射，反之为后向发射。前向发射火箭能量损失小，有助于提高其运载能力。

前向发射有牵引伞拖拽和重力出舱两种方式。后者靠火箭自身重力出舱，容易做到火箭大俯仰角离机，尽快建立点火姿态，并可将载机能量最大限度传递给火箭，提高入轨载荷质量［11］。

内装式发射火箭的出舱过程涉及复杂的两体耦合动力学。文献［3］利用Adams 和Solid⁃works 建立了载机、火箭和稳定伞组成的虚拟样机并进行了仿真，但未给出系统动力学的数学解析模型。文献［8］推导了火箭出舱过程的动力学模型，但是假设载机的运动状态恒定，未考虑火箭对载机的耦合影响。文献［9］直接给出火箭出舱过程的动力学模型，也未考虑火箭对载机的耦合影响。文献［12］将火箭和载机视作一个整体，考虑火箭在机舱内不同位置对系统整体质心的影响，分析了发射分离时“载机”的飞行品质。文献［13⁃16］研究了空射运载火箭的其他相关问题，重点不是机⁃箭耦合动力学。文献［17］设想在机舱内安装一个与火箭等直径的发射筒，火箭出舱运动被限制在该筒纵轴线上，建立了火箭出舱过程的机⁃箭两体耦合动力学模型。但实际上火箭出筒的末阶段，发射筒和箭体的接触面急剧减小，接触面上局部载荷急剧增大，火箭运动难以严格限制在发射筒纵轴线上，因此该文所考虑的情况偏于理想化。

国内外公开发表的文献中，针对内装式重力出舱机⁃箭两体耦合动力学进行建模研究的极少，且不够深入。美俄等航天强国已经试验成功的火箭重力出舱过程，机舱内没有发射筒，火箭直接置于舱底滑轨上，出舱过程会发生复杂的情况，譬如箭头上翘，此时火箭的相对运动自由度发生变化。本文即针对这些复杂情况，研究火箭重力出舱机⁃箭两体耦合动力学。

1 火箭出舱过程运动分析

火箭相对于载机的运动，可分为图1 所示的5个阶段，并可能出现多种异常情况。

图1 火箭出舱经历的正常阶段和可能发生的异常情况Fig.1 Normal stages and possible abnormal situations of the rocket exiting the cabin

阶段1 整箭在舱底滑行；阶段2 箭体紧贴舱底，但已部分出舱；阶段3 箭体出舱部分越过“临界点”后，箭头上翘，火箭通过舱尾的一个支点相对于载机滑行。因阶段3 火箭滑行的同时还有关于自身质心的姿态俯仰运动，故火箭与载机的唯一支点可能消失，箭体“飘起”，进入阶段4。阶段4 能否发生取决于一定的力学条件，后文详述。阶段5 表示火箭完全离舱。

阶段1 可能发生异常情况1⁃1，1⁃2，1⁃3，分别表示火箭在舱内“抬头”、“翘尾”、“整体飘起”。阶段2 可能发生异常情况2⁃1 和2⁃2，分别表示火箭“翘尾”和“整体飘起”。阶段3 可能发生异常情况3⁃1，表示火箭抬头角过大，箭头触碰舱顶。阶段4 可能发生异常情况4⁃1 和4⁃2，分别表示箭头触碰舱顶，以及箭腹触碰舱尾。

需说明的是，从静态观点看，图1 中阶段4和异常情况2⁃2 所描述的箭机相对运动相似，但从动态观点看，两者物理意义不同：阶段4 是阶段3 的自然延续，箭机之间唯一的支点消失，而异常情况2⁃2 表示在阶段2，火箭过早“整体飘起”，火箭很可能“回落”撞击舱底。同样，图1中阶段3 和异常情况4⁃2 所描述的箭机相对运动相似，但两者物理意义不同：阶段3 是阶段2 的自然延续，火箭与载机的“接触线”逐渐缩短退化为“支点”，而异常情况4⁃2 表示在阶段4，火箭相对于载机的“下落”运动致其腹部与舱尾发生“碰撞”。

综上所述：正常情况，箭机之间只会相对滑行，最后脱离接触，可能经历阶段1，2，3，4 或1，2，3 后进入阶段5。“异常情况”表示箭机之间发生“碰撞”，譬如“异常情况3⁃1，4⁃1，4⁃2”，或者有潜在的“碰撞”风险，譬如“异常情况1⁃1，1⁃2，1⁃3 和2⁃2”，本身不代表碰撞，但火箭有可能“回落”而撞击舱底。

2 火箭出舱过程机⁃箭多体动力学建模

图2、3 中，p和r分别为载机和火箭的质心。空射时飞行纵平面内的运动是主要的，本文仅研究该平面内的运动。

图2 载机重要几何参数Fig.2 Key geometry parameters of the aircraft

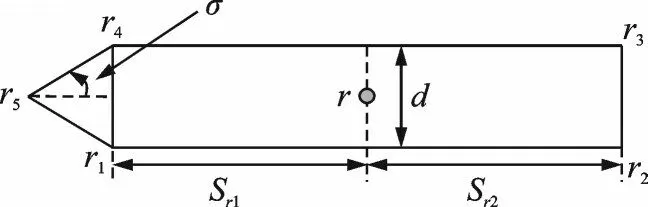
图3 火箭重要几何参数Fig.3 Key geometry parameters of the rocket

本文涉及5 个坐标系：地面惯性系oA xA yA、载机速度系oB xB yB、机体系oC xC yC、箭体系oD xD yD、箭体局部速度系oE xE yE，分别用A，B，C，D，E表示。坐标系A，B，C，D的定义及其变换关系见文献［18］，此处仅定义坐标系E：原点oE在火箭已出舱部分的几何中心，oE xE轴沿着该点速矢方向，oE yE轴垂直于oE xE且在竖直平面内，向上为正。

本文工作包括火箭固定在机舱内的建模和火箭解锁后出舱过程的两体系统建模。

空射前火箭固定在机舱内，此时可将载机⁃火箭视作一个刚体。解锁后进入阶段1～4，火箭和载机间有相对运动，须按两体问题处理。各阶段载机均有两个平动和一个姿态俯仰自由度，阶段1 和2 火箭有一个滑移自由度，阶段3 火箭有一个滑移和一个姿态俯仰自由度，阶段4 火箭有两个平动和一个姿态俯仰自由度。阶段1 和2 的力学模型形式相同，前者火箭受到的气动力为零，后者非零，故可把前者视作后者的特例，统一建模。阶段3 和4需分别建模。

2.1 火箭固定在机舱内时的系统动力学

式（4，5）在各阶段均成立，式（6）在阶段1 和2中均成立。

对于火箭固定在机舱内时的系统动力学，限于篇幅，本文略去推导过程，直接给出结果如下

式中：mp，mr分别为载机和火箭质量；Ip，Ir分别为载机和火箭关于各自质心的俯仰转动惯量；v为载机飞行速度；α为其迎角；P为载机发动机推力；Q，Y分别表示载机气动阻力和升力；M′Rp为载机气动俯仰力矩；g为重力加速度常数。

2.2 阶段1 和2 系统动力学

阶段1 和2，载机质心动力学

式中μ为舱底和火箭之间的滑动摩擦系数。

式中c3表示C系沿zC轴正方向的单位矢量。对于图1 所示飞行方向，按右手规则，zC轴正方向垂直于纸面向里。后文中涉及到某坐标系的z轴及其单位矢量均同理，不再逐一解释。

火箭姿态俯仰动力学

相关各式联立，可得

异常情况2⁃1 的发生条件（即判别公式）与异常情况1⁃2 的发生条件相同；异常情况2⁃2 的发生条件（即判别公式）与异常情况1⁃3 的发生条件相同。

2.3 阶段3 系统动力学

阶段3 如图4 所示。在阶段3，载机质心动力学和姿态动力学方程的一般形式，即式（8，18）仍成立。但因火箭对载机的作用力集中于舱尾支点p1，故式（18）中的Mfp可具体化，联立相关各式可得

图4 阶段3 机⁃箭关系详图Fig.4 Details of aircraft⁃rocket in stage 3

用变量s和λ描述火箭质心相对于载机质心的位矢如下

相关各式联立，可得

下面计算火箭受到的空气动力Rr。仍取火箭出舱部分几何中心r6点为气动力等效作用点，结合阶段3 的具体条件可得

2.4 阶段4 系统动力学

在阶段4，火箭与载机脱离接触，两者间无力的直接作用。载机的飞行动力学即常规的飞行器飞行力学。火箭相对于载机的动力学方程限于篇幅忽略推导过程，直接给出结果。系统动力学方程如下

出舱部分的局部攻角计算公式（57）仍成立。出舱部分受到的气动阻力、气动升力、局部动压的计算公式（32，33）仍成立，只是式（32）中k′的计算公式需作相应修改。

阶段4 过渡到阶段5 的标志是：箭头r5点穿越载机p1，p2两点连线，进入其右侧即舱外（参考图1）。设想以r5为始点，分别以p1，p2为终点，构造两个矢量，记为rp1r5和rp2r5，两者叉乘

3 数值仿真

空射过程仿真结果如图5～13 所示。图5～10仿真曲线上标注了倒三角、钻石形、小圆圈、五角星，其意义如下：倒三角之前的曲线表示载机带箭巡航；倒三角与钻石形之间的曲线表示阶段1；钻石形与小圆圈之间的曲线表示阶段2；小圆圈与五角星之间的曲线表示阶段3；五角星之后的曲线表示阶段4。

图5 载机飞行高度Fig.5 Flight height of the aircraft

表1 仿真入口参数Table 1 Input parameters for simulation

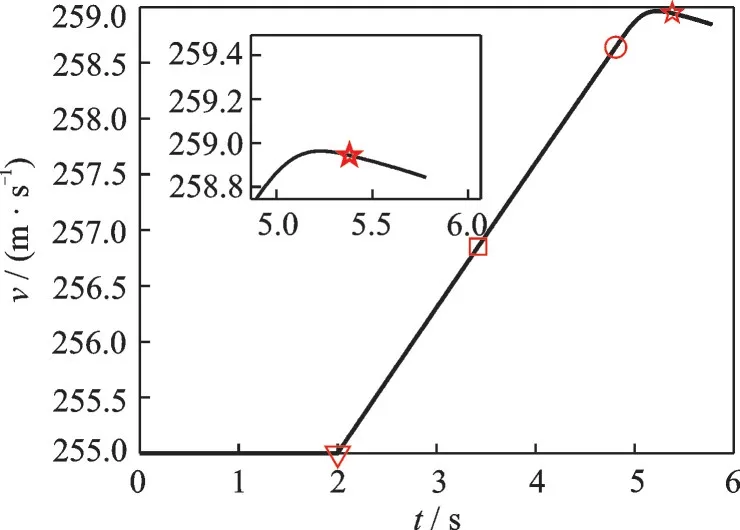
图6 载机飞行速度Fig.6 Flight velocity of the aircraft

图5、6显示，火箭出舱过程中，载机的飞行高度增量约为8 m，飞行速度增量约为3.84 m/s，是因为火箭将自身的一部分动量和机械能转移给载机的缘故。

图7中的η和ηr分别表示载机和火箭的姿态俯仰角。载机姿态俯仰角略有增加，这是因为火箭在舱内向后滑行，对载机施加抬头力矩；火箭的姿态俯仰角有大幅度增加，达到39.3°，原因是阶段3 中的“跷跷板”效应，火箭相对于载机有大幅度的抬头角λ。

图7 载机和火箭姿态俯仰角Fig.7 Pitch angles of the aircraft and the rocket

图8显示，阶段1和2中载机攻角单调增加。但进入阶段3后，因火箭对载机正压力的幅度开始减小，其对载机的抬头力矩也减小，载机在自身气动稳定力矩的作用下，迎角开始回落，直至终值（约21.95°）。

图8 载机迎角Fig.8 The attack angle of aircraft

图9 与图7 对应，实线和虚线分别是载机和火箭的俯仰角速率。火箭在离机时的俯仰角速率达到20.5 (°)/s。高达39.3°的离机俯仰角和20.5 (°)/s的俯仰角速率有利于火箭离机后尽快进入点火姿态。

图9 载机和火箭姿态俯仰角速率Fig.9 Pitch angle rate of the aircraft and the rocket

图10 显示，火箭在舱内的滑行呈加速趋势，离机时沿载机纵轴的速率达到20.2 m/s，有利于载机与火箭迅速拉开距离，减小载机尾流对火箭的干扰，也减小火箭点火对载机的安全威胁。并且由前述仿真结果数据估算，火箭离机后约2～3 s 即可达到近乎垂直的点火姿态，且与载机的水平距离达到约40～60 m 的安全值。

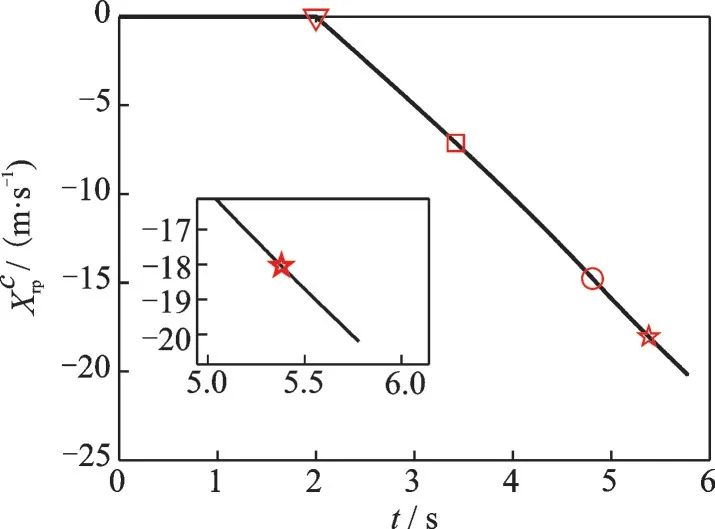
图10 火箭沿载机纵轴的滑行速度Fig.10 Sliding velocity of the rocket along the longitudi⁃nal axis of the aircraft body

图11～13是阶段3，4中的部分关键变量。图11显示变量s在5.38 s 时递减到5.58 m，此时火箭与载机脱离接触进入阶段4。对比图12，此刻火箭对载机的正压力分量fC2的幅值递减到零，火箭整体“飘起”。图13 是阶段4 中标志火箭离舱变量w′r5的曲线，可见从5.38 s 开始，该变量从-45 m2单调递增，直至5.78 s时，该变量过零点，此时火箭完全离舱。

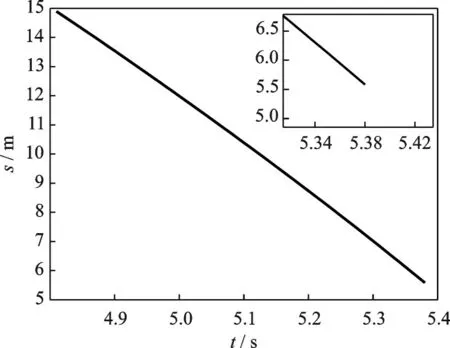
图11 阶段3 中变量sFig.11 Variable s in stage 3

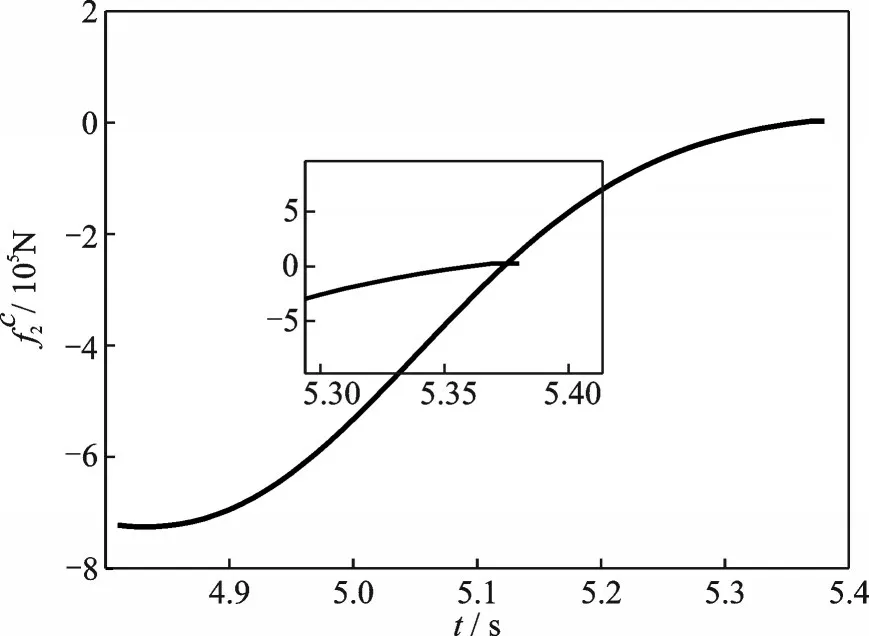
图12 阶段3 中火箭对载机的正压力Fig.12 Normal pressure on the aircraft by the rocket in stage 3

图13 阶段4 中火箭离机的标志变量Fig.13 Marking variable of the rocket separating from the aircraft in stage 4

仿真结果表明，火箭在舱内的运动经历了阶段1，2，3，4，最终进入阶段5，机箭分离。

4 结论

本文研究了以运输机为平台的内装式空射运载火箭重力出舱过程载机⁃火箭两体动力学。将正常出舱过程顺次分为4 个阶段，建立了各阶段的动力学模型，给出了各阶段过渡的力学条件。给出了多种异常情况，并分析了发生异常情况的力学或几何条件。对出舱过程的两体系统进行了数值仿真。

限于篇幅，仿真只展示了一组典型设计参数和发射初始条件下，机⁃箭系统顺次经历阶段1，2，3，4，直至进入阶段5，仿真正常结束。

工程上，可根据载机和火箭的多种设计参数（譬如质量、几何和气动等参数）和发射参数（譬如火箭在载机中的初始安放位置、载机的巡航高度和速度等），运用本文提供的数学模型进行仿真，根据仿真结果排除不合理设计参数和发射参数，保留合理参数，建立相应的数据库，为我国发展空射运载火箭技术提供参考。

本文只研究了纵向平面内的动力学，且没有考虑控制输入（譬如载机油门和升降舵）对空射过程的影响。后期需进一步考虑载机和火箭横侧向运动，建立更完整的力学模型，并深入研究载机飞行控制律，以改善空射过程飞行品质，优化火箭离机状态。另外，异常情况下火箭与载机的触碰动力学也值得深入研究。