一道数学竞赛题的证明、应用与推广
杨 威
(合肥工业大学数学学院,合肥230009)
一道数学竞赛题的证明、应用与推广
杨 威
(合肥工业大学数学学院,合肥230009)
介绍了一道高等数学竞赛题的五种证明方法并举例说明其应用,另外介绍了其推广.
竞赛题; 一题多解; Rolle定理; 应用; 推广
1 竞赛题
东南大学2010年高等数学竞赛的第五题[1]是
设函数f(x)在[a,b]上连续,在(a,b)内二阶可导,证明:对每个c∈(a,b),存在ξ∈(a,b),使得
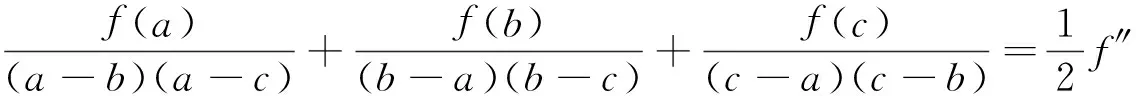
(1)
本文首先介绍这道试题的五种不同证法,然后举例说明此试题的某些应用,最后再介绍这道试题的推广.
注 本题多次被选为研究生入学考试、各种竞赛题,如2005年四川大学研究生入学试题,中央财经大学2010年高等数学竞赛试题:设函数f″(x)在[a,b]上存在,a 证法1[1]构造辅助函数法.构造辅助函数 则F(x)在[a,b]上连续,在(a,b)内二阶可导,且有F(a)=F(b)=F(c)=0.由Rolle定理知,存在ξ1∈(a,c),ξ2∈(c,b),使得F′(ξ1)=F′(ξ2)=0,再由Rolle定理知,存在ξ∈(ξ1,ξ2)⊂(a,b),使F″(ξ)=0.即 (1) 证法2 构造辅助函数法. 构造辅助函数 则G(x)在[a,b]上连续,在(a,b)内二阶可导,且G(a)=G(b)=G(c)=0,仿证法1,两次运用Rolle定理知,存在ξ∈(a,b),使得G″(ξ)=0.而 将行列式按第四列展开,可得 将上面两个三阶行列式展开并整理即得(1)式. 证法3 利用Cauchy中值定理及Lagrange中值定理,令 F(x)=f(a)(c-x)+f(c)(x-a)+f(x)(a-c), G(x)=(a-x)(x-c)(c-a), 则F(c)=G(c)=0,对F(x),G(x)在[c,b]上运用Cauchy中值定理知,存在ξ1∈(c,b),使得 (2) 再令 H(x)=f(x)-f(a)+f′(ξ1)(a-x), K(x)=[(a-ξ1)-(ξ1-x)](x-a), 则H(a)=K(a)=0, 对H(x),K(x)在[a,c]上运用Cauchy中值定理知,存在ξ2∈(a,c),使得 (3) 再由Lagrange中值定理知,存在ξ∈(ξ2,ξ1)⊂(a,b),使 (4) 由(2),(3),(4),所以 即 整理后即得(1)式. 证法4 利用Taylor公式,将f(a),f(b)分别在x=c处展开,得 (5) (6) 其中ξ1介于a与c之间,ξ2介于b与c之间,由(5),(6)知 (7) (8) (7)+(8)并整理得 由于 故由关于导函数介值性质的Darboux(达布)定理知,存在ξ∈(ξ1,ξ2)⊂(a,b),使 因此,要证的(1)式成立. 证法5 待定k值法.若记 则有 f(a)(b-c)+f(b)(c-a)+f(c)(a-b)+K(a-b)(b-c)(c-a)=0, 令 φ(x)=f(x)(b-c)+f(b)(c-x)+f(c)(x-b)+K(x-b)(b-c)(c-x), 则φ(a)=φ(b)=φ(c)=0,两次运用Rolle定理知,存在ξ∈(a,b),使得φ″(ξ)=0而 φ″(x)=f″(x)(b-c)-2K(b-c). 结论(1)可以用来解不少相关高等数学问题,下面仅举三个例子予以说明. 例1[2](大连理工大学2005年研究生入学考试题;天津市2005年大学生数学竞赛试题) 设函数f(x)在[a,b]上连续,在(a,b)内二阶可导,证明:存在ξ∈(a,b),使得 (9) 证 只需要在(1)中取c=(a+b)/2并整理即可得到(9). 证 由题设易知f(x)的最小值在(0,1)内取到,故可在(1)中取a=0,b=1,并设f(c)=-1,于是由(1)可知 由于 例3[4](华中师范大学2003年研究生入学考试题) 设f(x)在 [a,b]上二阶可导,过点A(a,f(a))与B(b,f(b))的直线与曲线y=f(x)相交于C(c,f(c)),其中a 证 由(1)可知 (10) 因为A,B,C三点共线,所以 即 (11) 由(10),(11)及a 前面所讨论的试题的一般形式为 设函数f(x)在 [a,b]上连续,在(a,b)内n阶可导,若xi∈[a,b],i=0,1,2,…,n,则存在ξ∈(a,b),使得 (12) 事实上,等式(12)表明了函数f(x)在节点 x0,x1,x2,…xn处的n阶差商与f(x)的n阶导数之间的关系,其证明可见数值分析教材,如[5],[6]等. [1] 东南大学高等数学教研室.高等数学试题分析[M]. 2版.南京:东南大学出版社, 2014. [2] 叶国菊,赵大方.数学分析学习与考研指导[M]. 北京:清华大学出版社, 2009. [3] 许康,陈强,陈挚,陈娟编译.前苏联大学生数学奥林匹克(上篇)[M]. 哈尔滨:哈尔滨工业大学出版社, 2012. [4] 钱吉林.数学分析题解精粹[M]. 武汉:崇文书局, 2003. [5] 关治,陆金甫. 数值分析基础[M]. 北京:高等教育出版社, 1998. [6] 王能超. 数值分析简明教程[M]. 2版. 北京:高等教育出版社, 2003. [7] 苏化明,禹春福. 一类中值问题的行列式解法[J]. 大学数学, 2013,29(2):143-146. The Proof, Application and Promotion of a Maths Contest YANGWei (School of Mathematics, HeFei University of Technology, Hefei 230009, China) This paper introduces an advanced mathematics contest problem of the five methods and examples to illustrate its application, in addition to the introduction of its promotion. competition problem; multiple solutions; Rolle theorem; application; promotion 2016-07-12; [修改日期] 2016-09-01 杨威(1979-)男,硕士,讲师,主要从事高等数学教学与研究、数据加密、股票概率学研究. Email:shuxueyangwei@126.com O172 C 1672-1454(2016)05-0112-04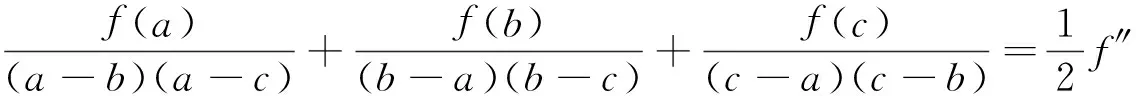
2 试题的五种证明
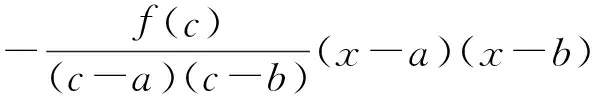
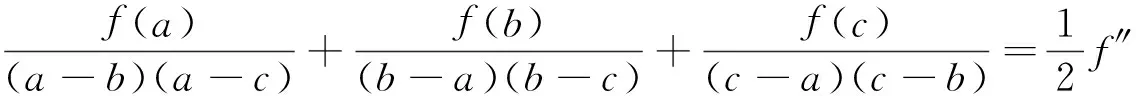
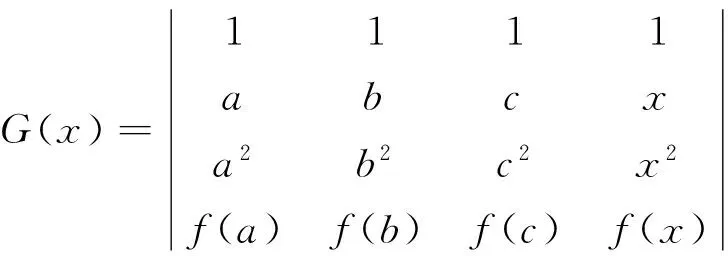
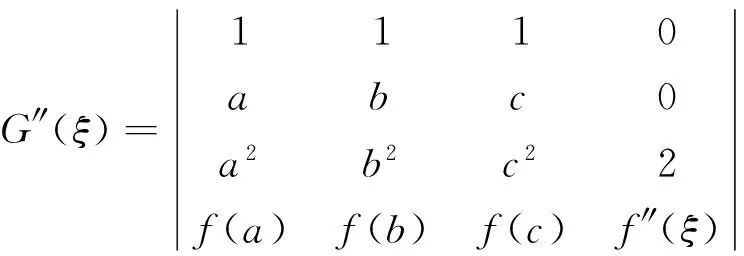
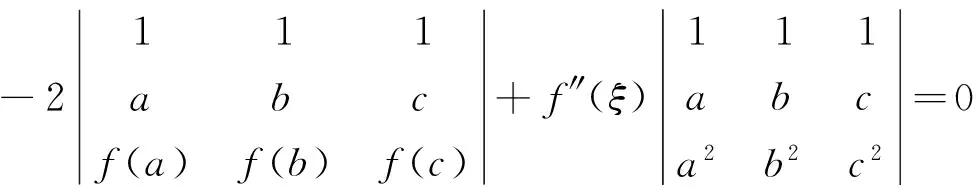


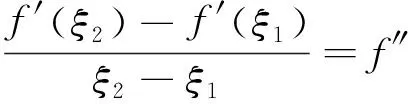
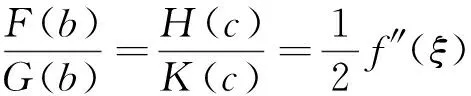
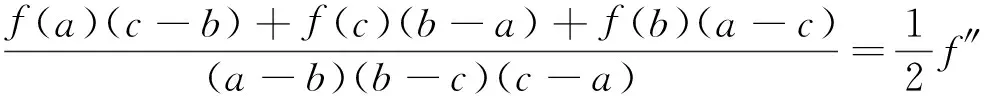
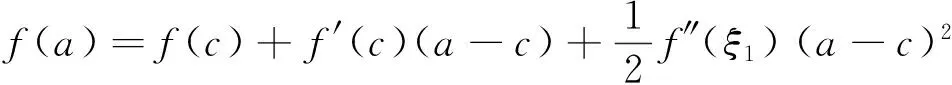
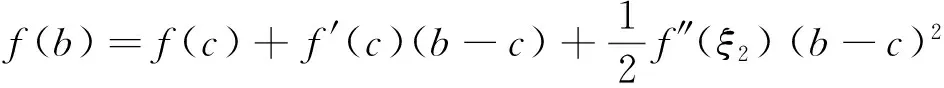
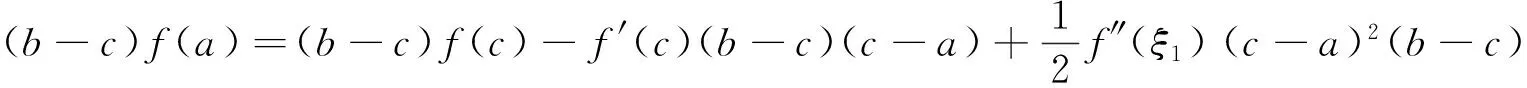

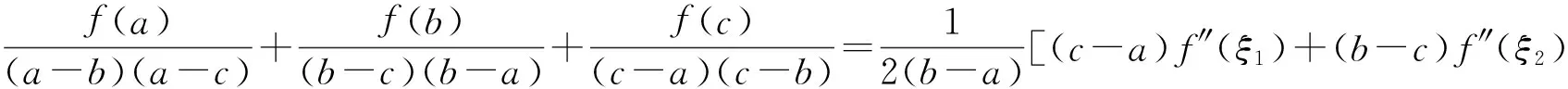
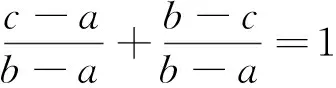
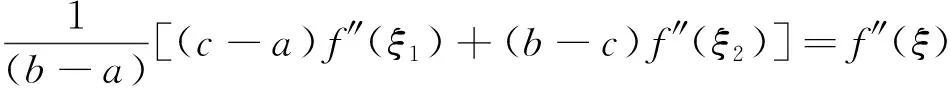


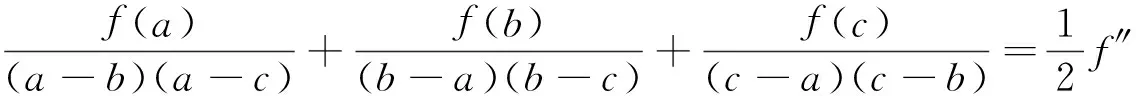
3 应用举例
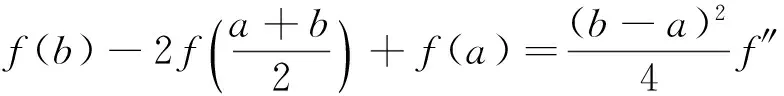
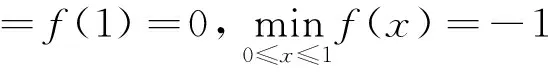
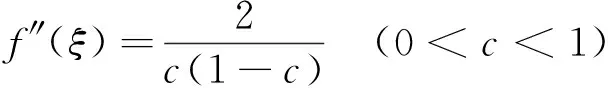
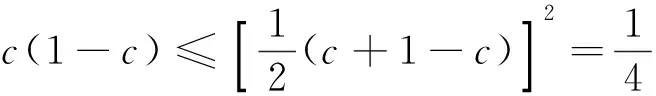

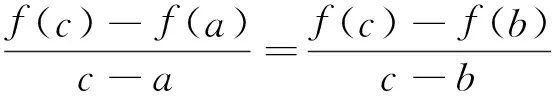

4 推 广