第二重要极限的一种简易变形

牛传择, 桑 波, 颜 红

(1.聊城大学数学科学学院, 山东聊城252059； 2. 聊城市东昌中学,山东聊城252000)



第二重要极限的一种简易变形

牛传择1, 桑 波1, 颜 红2

(1.聊城大学数学科学学院, 山东聊城252059； 2. 聊城市东昌中学,山东聊城252000)

利用无穷小量,给出了第二重要极限的一类变形.讨论了该变形在求不定极限中的应用技巧,利用带佩亚诺型余项的泰勒展开式,该变形可以较快的解决一些求不定极限的问题.结合历年考研试题阐明该变形在求1∞型不定式极限中的优势.

第二重要极限； 无穷小量； 泰勒公式

1 引 言

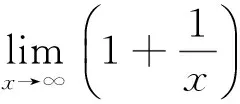
2 主要结果

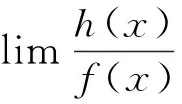
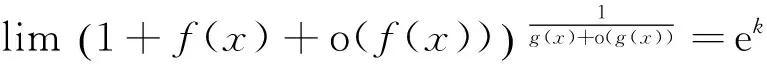
(1)

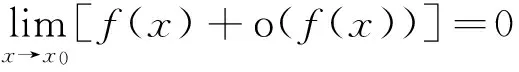
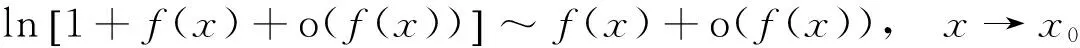
故

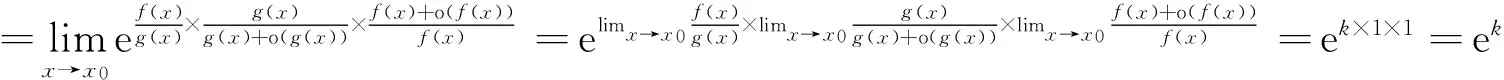
利用与定理1的证明中相同的方法，也可证明下面的定理2.

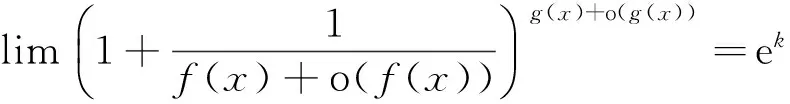
(2)

特别地，作为定理1，2的特殊情形，有

推论1 设limf(x)=0,则

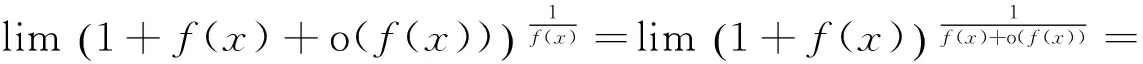
(3)

推论2 设limf(x)=∞,则

(4)

(5)

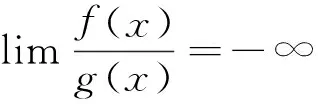
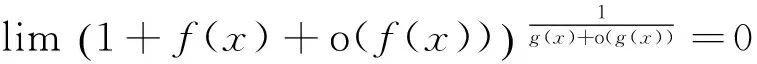
(6)

(7)

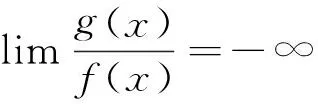
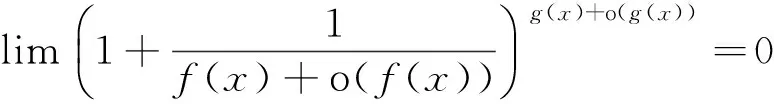
(8)

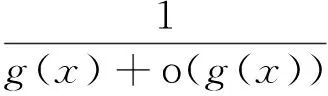
3 应用举例

结合四个历年考研试题，阐明如何利用定理1、定理2计算1∞型不定式极限.

分析 这是一个1∞型不定式极限，利用泰勒公式将cos2x+2xsinx化为1+f(x)+o(f(x))的形式.

解 利用泰勒公式，因为

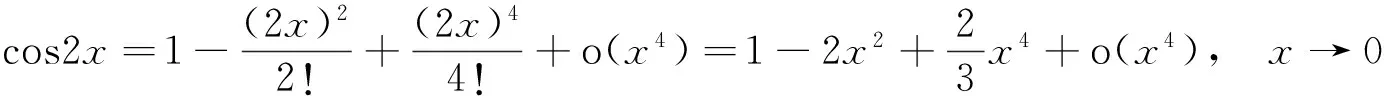
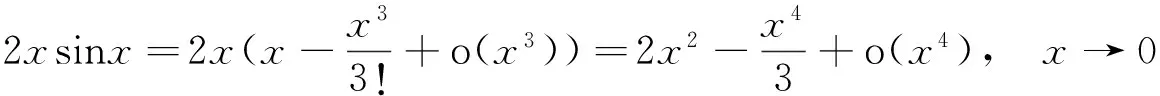
所以

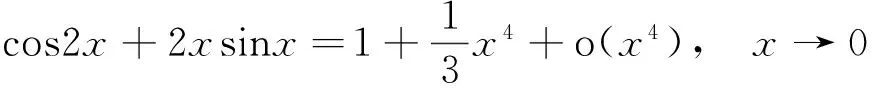
故

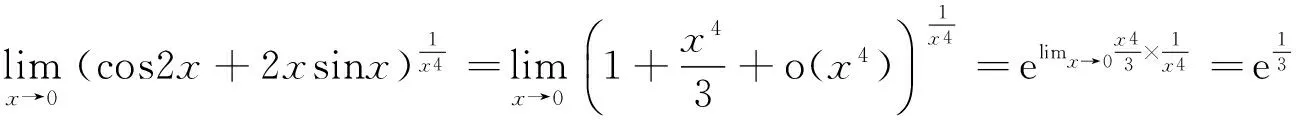
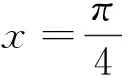
解 因为

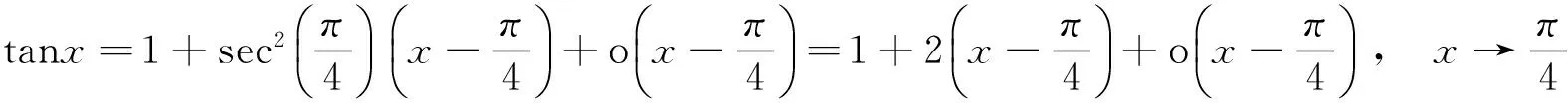
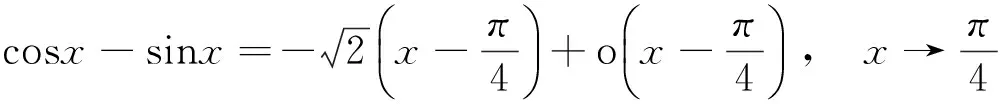
所以

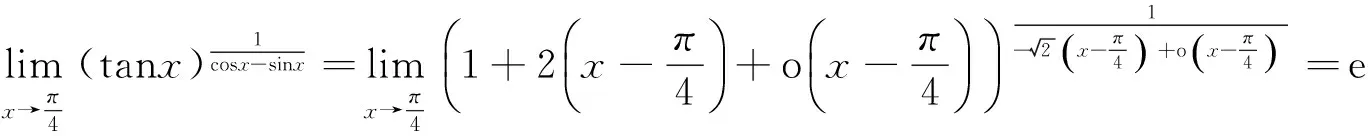
注 例2有更简单的解法.

解 因为

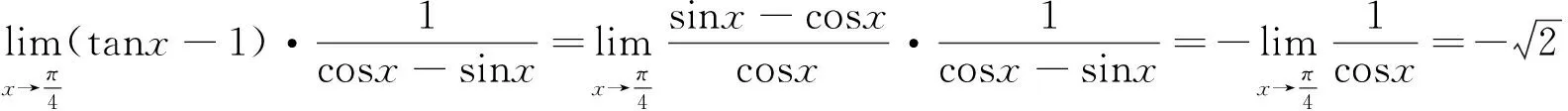
所以

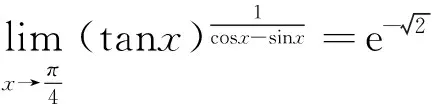
这是因为对1∞型不定式极限limf(x)g(x)，有

limf(x)g(x)=lim(1+f(x)-1)g(x)=elim(f(x)-1)g(x).

事实上，上式将求1∞型不定式极限limf(x)g(x)转化为求0·∞型不定式极限lim(f(x)-1)g(x).例2中，经过化简，(f(x)-1)g(x)的极限容易求得，所以注解中的解法较为直接.但是一般情形下求解0·∞型不定式极限lim(f(x)-1)g(x)有可能较为复杂.

分析 因为x→0时,ln(1+x)与x是等价无穷小量，且ex-1→0,所以这是一个1∞型不定式极限.

解 利用泰勒公式,因为

所以

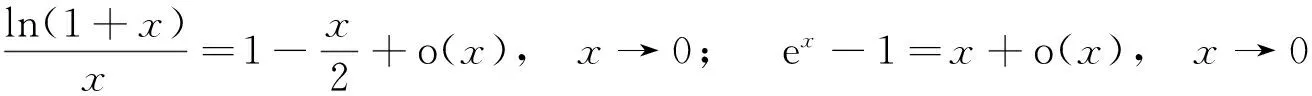
因此

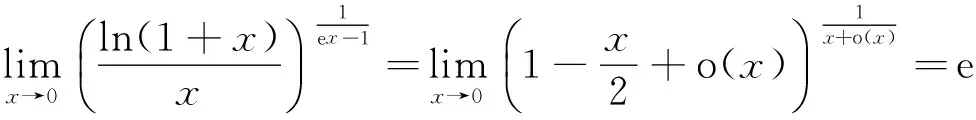
解 利用泰勒公式，因为

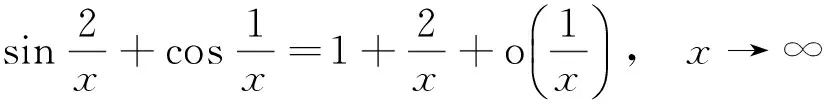
所以

通过4个典型考研试题的解答过程可以看出，在求1∞型不定式极限时，结合泰勒公式，定理1、定理2避免了洛必达法则的反复求导，是一种值得采用的解决问题的方法.

4 结 论

[1] 同济大学数学系.高等数学[M]. 6版.北京：高等教育出版社,2012.

[3] 邓雪,赵俊峰.洛必达(L’Hospital)法则在求1∞型极限中的应用[J]. 大学数学，2006,22(4)：158-160.

[4] 华婷,文传军.解析第二极限的三步骤法 [J].常州工学院学报,2014,27(6)：42-45.

[5] 王秀旺,周贵祥.第二重要极限的应用技巧及推广[J].数学学习与研究：教研版,2010(61)：94-95.

A Simple Deformation of the Second Important Limit

NIUChuan-ze1,SANGBo1,YANHong2

(1. School of Mathematical Sciences, Liaocheng University, Liaocheng Shandong 252059, China;2. Dongchang Middle School, Liaocheng Shandong 252000, China)

Using infinitesimals, a deformation of the second important limit is proposed. Application of such deformation in computing indeterminate limits is discussed. Using this deformation, combined with Taylor expansions with the remainder of the Peano form, some indeterminate limit problems can be resolved quickly. The advantages of such deformation in solving limits of the form 1∞are classified through questions in the postgraduate entrance examinations over the years.

the second important limit; infinitesimals; Taylor’s formula

2016-06-22； [修改日期] 2016-07-19

聊城大学本科教学改革研究项目(311161522)；国家自然科学青年基金项目(11401285)

牛传择(1985-),男，博士，讲师，从事基础数学研究.Email: niuchuanze@lcu.edu.cn

O13

C

1672-1454(2016)05-0105-04