关于对换的几个结论
陈健夫
(广州大学数学与信息科学学院, 广州510006)
关于对换的几个结论
陈健夫
(广州大学数学与信息科学学院, 广州510006)
主要为了解决一个置换可以表示为至少多少个对换的乘积的问题.通过使用初等方法包括数学归纳法和反证法证明了几个引理,并用这几个引理解决了问题,同时给出一个应用.
对换; 置换; 置换群
1 引 言
我们知道,一个置换总可以表成一些对换的乘积,并且这样的表示可能不唯一.现在有一个问题,一个确定的n元置换可以表示为至少多少个对换的乘积?由最小数原理知道,这个问题是有意义的.本文没有使用高级的数学工具,仅是综合运用基本的逻辑方法,包括数学归纳法和反证法证明了用于解决这个问题的8个引理,并且这些引理本身也是很有益的,最后再给出这个结论在一个组合问题上的应用.
2 预备知识
定义1 一个有限集到自身的一一映射叫做一个置换.
定义2 有限集的一个把元素a1变到a2,a2变到a3,…,an-1变到an,an变到a1,并且其他元素不变的置换
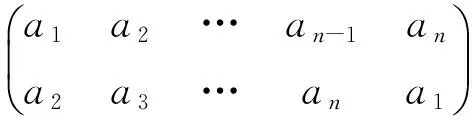
叫做一个n-循环置换,并称其阶为n.
定义3 一个2-循环置换叫做一个对换.
定义4 如果两个循环置换无公共元素,则称这两个循环置换不相连.
定义5 如果集合A有两个置换σ1和σ2,规定这两个置换的乘积为σ1σ2:x→σ2(σ1(x)),x∈A.换言之,乘积运算是从左往右进行的.
定理1 在不考虑顺序的情况下,一个置换可以唯一地表成若干个不相连的循环置换的乘积.
定理2 置换的奇偶性不变.即一个置换表成对换的乘积时,这些对换个数的奇偶性不变.
定义6 一个置换如果可以表成奇数个对换的乘积,则称这个置换为奇置换.否则,称为偶置换.
定理1,2的证明在一般的抽象代数学教材都会有.对于定理1,亦可以参看文献[1]中的证明.对于定理2的证明,可以参看文献[2]中的相关内容,文献[2]中证明该定理时使用了一个结论,即一个自然数排列施行一个对换,排列的奇偶性会改变,这个结论可以在文献[3]中找到证明,但文献[4]亦给出了比较新颖的证明方法,建议读者参考.
3 8个引理及其证明
引理1 一个n-循环置换可以表成n-1个对换的乘积.
证 对于任意一个n-循环置换
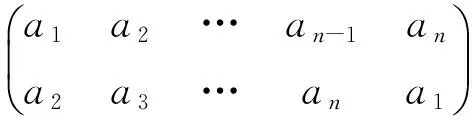
可以发现
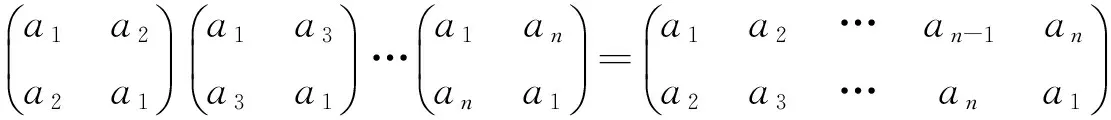
左边的对换个数为n-1.
在下面的引理中,除非情况是自明的,否则提到一个n-循环置换或一个n元置换时均假定集合中只有n个元素.
引理2 一个n-循环置换
右乘以一个对换,可以得到一个置换,该置换可以表成两个不相连循环置换的乘积,并且这两个循环置换的阶之和为n.
证
右乘以任意对换
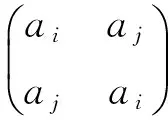
为了书写方便,不妨认为n≥5,并且ai,aj都不等于a1,a2,和an,这时可以得到置换
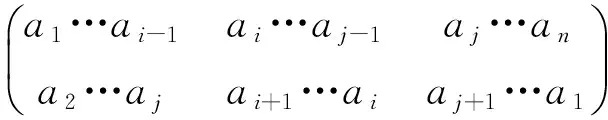
不难发现,这个置换可以表成
和
的乘积,这两个置换是不相连的循环置换,并且它们阶数的和等于n.如果ai,aj可以是a2,a1和an中的某一个,事实上,我们只需要重新对集合的元素命名,使得原来以i,j为下标的元素改变其下标变成不等于1,2和n即可.因为本质上,集合的元素本身与用什么符号表示并没有关系.
如果n≤4,只需逐个进行验证,总共也只有几种情况,这里不一一列出了.
引理3 如果一个置换π表成两个不相连的循环置换
和
的乘积,把π右乘以一个对换

ai是第一个循环置换中的元素,bj是第二个循环置换中的元素,那么得到一个n+m-循环置换.
证 结论其实相当显然.为了书写方便,不妨认为i≠1,2,n,j≠1,2,m,并且m,n≥5,那么π右乘以
后可以得到
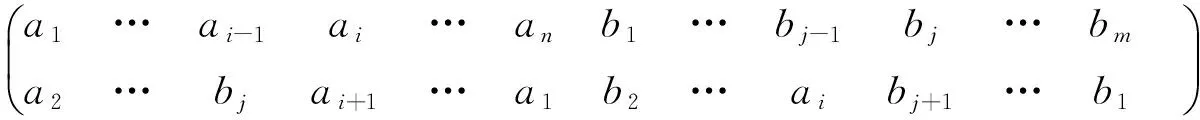
这就是一个n+m-循环置换.对于i=1,2或n, j=1,2或m,道理跟引理2的证明是一样的,可以对集合的元素重新命名,使之变为方便书写的情况.对于m,n≤4的情况,只需逐个验证,证明本质上是一样的,这里不一一列出了.
引理4 如果一个置换π可以表为至少k个对换的乘积,那么对该置换还原最后一次对换,还原成π′,那么π′可以表为至少k-1个对换的乘积.
证 反证法.假设不然,π′可以表为至少k-3或k-5…或1或0个对换的乘积,由于对于k-5或以下的情况,可以对2个相同的元素一直施加对换,使得π′表成k-3个对换的乘积,马上推出,π′可以表为k-3个对换的乘积(由定理2知道,一个置换可以表成的对换个数的奇偶性不变,所以一个置换可以表成的对换数相差一个偶数).下面几个引理的证明都会用到这样的反设,下面不再做说明.
那么,这时对π′重做刚才还原的对换,重新得到π,推出π可以表为k-2个对换的乘积,这与π可以表为至少k个对换的乘积矛盾.
引理5 一个n-循环置换
可以表为至少n-1个对换的乘积.
证 引理1已经说明了一个n-循环置换可以表为n-1个对换的乘积.下面证明这是最少需要对换的次数,也就是说,不能通过施加少于n-1个对换得到一个n-循环置换.
反证法.假设不然,n-循环置换
可以表为至少n-3个对换的乘积.此时,对π还原最后一次的对换,得到π1,由引理2知道,π1可以表为两个不相连循环置换的乘积,并且由引理4推出,π1可以表为至少n-4个对换的乘积.再对π1进行一次还原,得到π2,这次还原的对象不可能是两个不相连循环置换中各自取出的元素,否则根据引理3,会得到一个n-循环置换,而这个n-循环置换可以表为至少n-5个对换的乘积,这与我们的假设矛盾.所以,第二次还原的对象必须是其中一个循环置换的2个元素 ,那么π2就“分裂”成三个不相连循环置换的乘积.这样的操作一直进行下去,最后会经过n-3次还原得到恒等变换
但是根据上面的过程,我们实际上只“分裂”出n-2个循环置换,这意味着n元恒等变换表为n-2个不相连循环置换的乘积,但事实上n元恒等变换唯一地表为n个1-循环的乘积,于是得出矛盾.
引理6 一个n-循环置换
添加一个元素b进去,得到
是一个新的n+1元集合的置换,那么π可以表为至少n-1个对换的乘积.
证 反证法.假设不然,那么π可以表为n-3个对换的乘积.这时对π右乘以一个对换
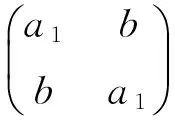
得到
这是一个n+1-循环置换,可以由n-2个对换相乘得到,但由引理5知道,π′可以表为至少n个对换的乘积,矛盾.
引理7 设任意n元置换
可以表为至少s个对换的乘积,对于任意一个m-循环置换
可以表为至少m-1个对换的乘积,a1a2…an和b1b2…bm-1bm没有共同元素,
是新的n+m元集合中的置换,那么π=可以表为至少s+m-1个对换的乘积.
证 第二数学归纳法.①当n=1时,由引理6知道命题成立.
②设当n≤k时命题成立,考察n=k+1的情况.
对于k+1元置换
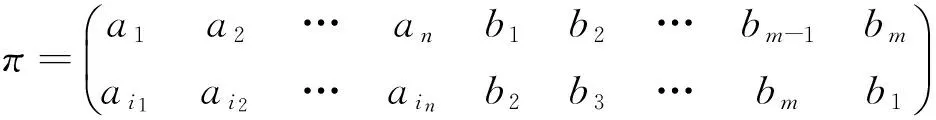
设其可以表为至少s个对换的乘积,由定理1知道,π可以表为若干个不相连循环置换的乘积,不妨从中抽出一个q-循环置换

其他循环置换并起来得到

那么
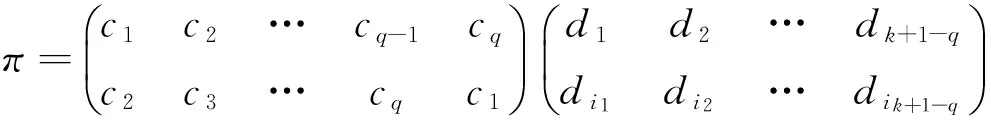
由归纳假设可以知道
可以表为至少s-q+1个对换的乘积(要注意,这是在仅有d1d2…dk+1-q这些元素的集合的意义下讨论的).
下面往证

可以表为至少s+m-1个对换的乘积.
反证法.假设不然,π′可以表为s+m-3个对换的乘积,那么现在对π′右乘以一个置换
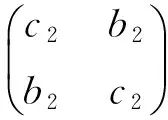
得到π*,由引理3知,π*可以表为q+m-循环置换
和
的乘积,这两个置换没有公共元素,并且这可以由s+m-2个对换相乘得到.但由归纳假设立得π*可以表为至少q+m-1+s-q+1=s+m个对换的乘积,推出矛盾,反证结束.于是证得对于n=k+1的情况命题成立.
引理8 如果置换π′表为n个不相连的循环置换π1π2…πn的乘积,而π1π2…πn分别可以表为至少a1a2…an个对换的乘积,那么π′可以表为至少a1+a2+…+an个对换的乘积.
证 数学归纳法:①当n=1时,由引理4知道命题成立.
②设当n=k时命题成立,考察n=k+1的情况.因为由假设知道π=π1π2…πk可以表为至少a1+a2+…+ak个对换的乘积,由引理7立即可以得到π′=π1π2…πkπk+1可以表为至少a1+a2+…+ak+ak+1个对换的乘积.
4 结 论
现在重新回到我们一开始想要解决的问题:一个n元置换可以表示为至少多少个对换的乘积?由引理8就可以容易得到答案,因为一个n元置换可以唯一地表成若干个不相连的循环置换的乘积,如果这些不相连的循环置换有k个,那么这个n元置换可以表成的对换乘积的最小个数等于这些循环置换各自可以表成对换乘积的最小个数之和,由引理5马上就可以知道,这个数就是n-k,于是我们有定理3.
定理3 如果一个n元置换唯一地表成k个不相连的循环置换的乘积,那么这个置换可以表成至少n-k个对换的乘积.
所以我们最初的问题便解决了,并且引理1就给出了对换的办法.下面给出该结论的一些应用.
5 应 用
有这样一类智力题,给出一列乱序的数码,要把它排成顺序数码,每次只能对其中两个数码进行对换,问最少要对换多少次,应该怎样对换.比如把序列

排成

最少要对换多少次.这个问题实质就是给出一个置换
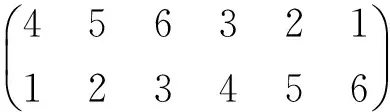
问这个置换可以表成至少多少个对换的乘积.由定理3知道,只要找出其可以表成不相连循环置换的个数就可以了.因为
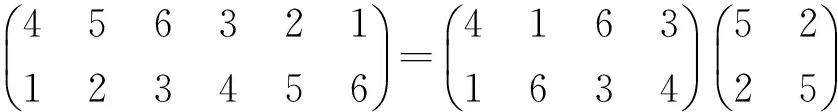
不相连的循环置换有2个,所以答案就是可以表示成至少6-2=4个对换的乘积,并且按照引理1的做法,即先把4和1对换,再把4和6对换,再把4和3对换,最后再把5和2对换.虽然这是只有6个数的序列,恐怕单纯通过穷举就不容易解出了.定理3就保证能够很容易知道最少需要对换多少次,并且用引理1就可以给出对换的方法.如果对于特别长的序列需要排序,设计算法使用计算机去找出这些不相连的循环置换就可以了.
[1] 陈健夫.循环置换分解定理的一个证明及其应用[J].大学数学,2015,31(4):95-98.
[2] 杨子胥.近世代数[M].北京:高等教育出版社,2000.
[3] 焦荣政.对换改变排列奇偶性的一个定量证明[J].大学数学,2009,25(6):174-176.
[4] 张禾瑞,郝炳新.高等代数[M].北京:高等教育出版社,2007.
Some Conclusions about Transposition
CHENJian-Fu
(School of Mathematics and Information Science, GuangZhou University, Guangzhou 510006, China)
This article solves a problem that how many transpositions are needed to denote a permutation at least. I give and prove several lemmas used to solve this problem by fundamental methods including mathematical induction and reduction to absurdity. At the meantime, I give an application related to combinatorics.
transposition; permutation; permutation group
2016-03-18; [修改日期]2016-06-01
陈健夫(1995-),男,本科生,数学与应用数学专业.Email:jmchenjianfu@126.com
O152
C
1672-1454(2016)05-0121-06

