一个二项式扩展模型及其在椭圆周长逼近中的应用

冯有宽

(内蒙古人力资源和社会保障厅，呼和浩特010055)



一个二项式扩展模型及其在椭圆周长逼近中的应用

冯有宽

(内蒙古人力资源和社会保障厅，呼和浩特010055)

针对无法用初等函数精确表示的椭圆周长级数展开式，首次提出了一个含有3参数的二项式逼近模型；讨论了这一模型用于逼近椭圆周长的基本方法，进而得到了5个结构紧凑的近似计算公式；通过实例分析论证了公式的精确度及其实用性.

二项式； 扩展模型； 函数逼近； 椭圆周长

1 引 言

众所周知，椭圆周长不能表示为精确的初等公式，通常表示为椭圆积分形式及其级数展开式[1].一个常用的级数展开式是

(1)

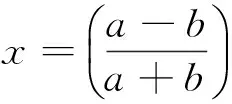
为了方便计算，许多学者以上述级数展开式为基础，对椭圆周长近似计算问题作了进一步探索，提出了不少近似公式[2].其中，1914年印度数学家拉马努金(S. Ramanujan ，1887-1920)给出了一个简洁而实用的近似公式，即

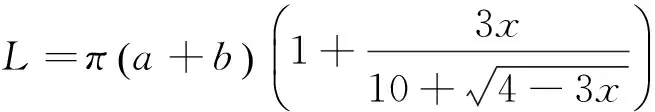
(2)

这个公式形式简洁，精度较高，呈现出数学的美感，因而得到了广大数学爱好者的普遍认可.但公式的推导过程却不得而知，未查阅到相关资料.

在研究椭圆周长近似计算问题中，我们用二项式的一个扩展模型逼近椭圆周长，不仅得到了拉马努金给出的近似公式，还可以得到更多、更精确的近似公式.本文介绍了这一模型及其在椭圆周长逼近中的应用.

2 一个二项式扩展模型

牛顿二项式定理一般可表示为

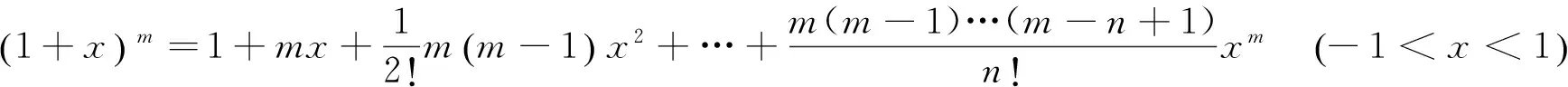
(3)

式(3)中x为变量，m为参数.

随着变量x和参数m的取值不同，右端的级数展开式可分别呈现出几何级数、正项级数、交错级数等不同类型的级数，具有逼近函数的基本特性.但由于参数少，在应用范围上受到了限制.为此，在式(3)基础上加入了k和g两个参数，变为以下形式

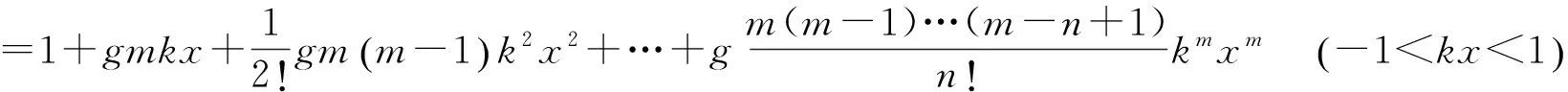
(4)

式(4)与式(3)相比，由一个参数增加到三个参数，增强了实用性；等式左端包含二项式、右端是按照二项式定理展开的多项式，我们称其为二项式的一个扩展模型.

3 二项式扩展模型在椭圆周长逼近中的应用

3.1 基本逼近方法

用函数p(x)近似表示已知函数f(x)，并求出两者间的误差，这是函数逼近的基本问题[3].用二项式扩展模型逼近椭圆周长，只需将椭圆周长公式中的级数部分(或级数部分运算后生成的新级数)作为被逼近函数，即

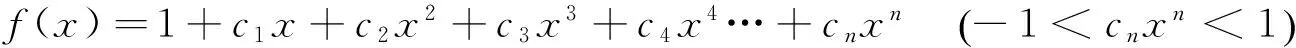
(5)

将二项式扩展模型作为逼近函数，即

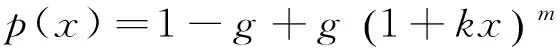
(6)

按照式(4)与式(5)级数展开式同次幂系数相等的规则，可得到以下方程组及其g,k,m三个参数的求解结果，即

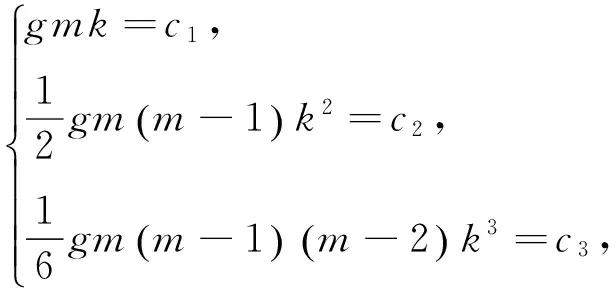
(7)

将三个参数代入式(6)可得到逼近函数p(x)，用p(x)近似表示f(x)便可获得不同形式的椭圆周长近似公式.

3.2 具体逼近方法与实例

3.2.1 直接逼近

将式(1)括号内的级数展开式设定为被逼近函数，即

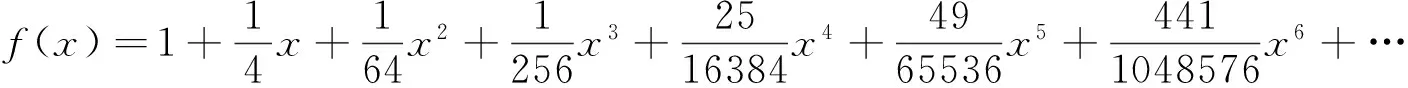
(8)

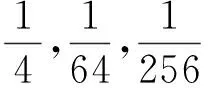
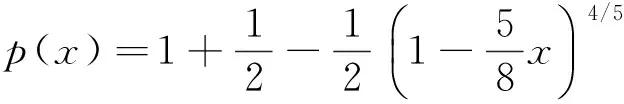
替换式(8)并回代到式(1)可得到椭圆周长的第一个近似公式，即

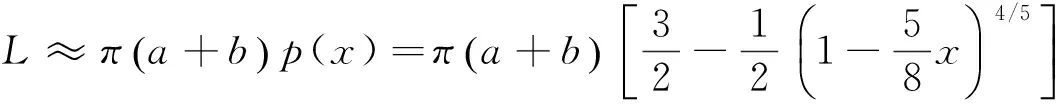
(9)

3.2.2 分母中逼近

式(8)运算后可变为

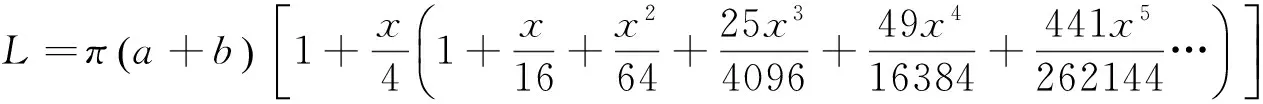
(10)

按照级数运算规则，式(10)可变为分母中包含级数的形式，即

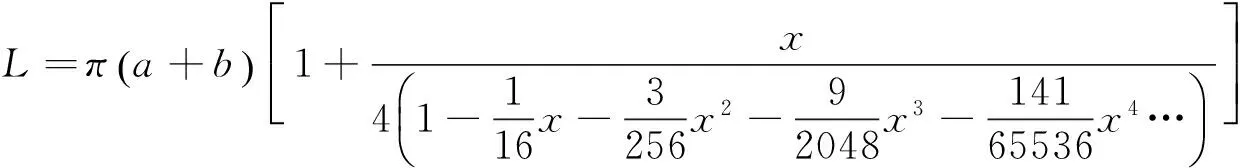
(11)

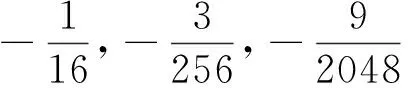
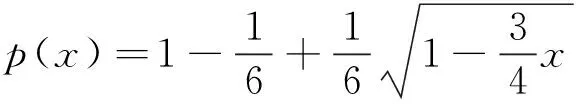
替换被逼近函数并代入式(11)可得到椭圆周长的第二个近似公式，即

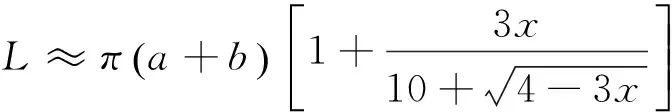
(12)

这个公式与拉马努金给出的公式完全相同.拉马努金曾经给出了几千个数学公式，很多公式都没有推导过程，我们不敢妄加猜测他的思想过程，但相同的结果却值得我们深思.

如果按照分母中逼近的上述思路，将式(11)进一步运算还可变化为以下形式

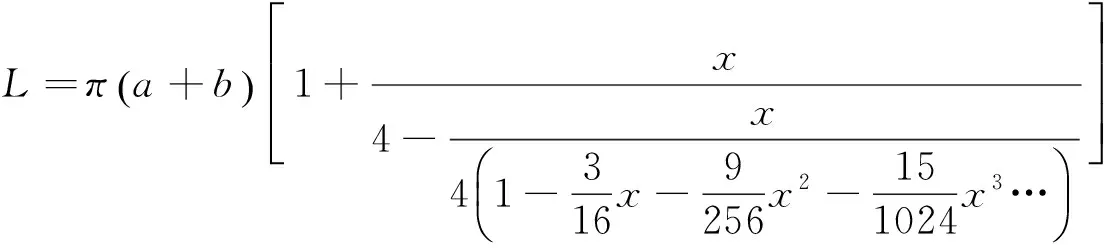
(13)

将式(13)小括号内的幂级数多项式作为被逼近函数f(x)，用相同的方法可得到第三个近似公式，即

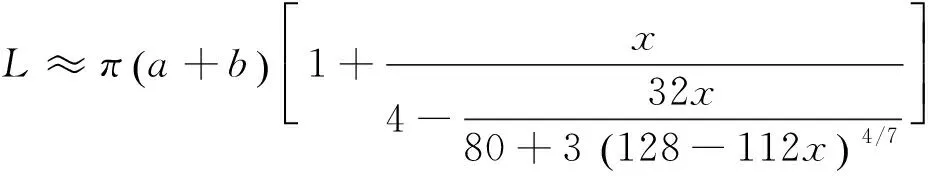
(14)

3.2.3 分子分母分别逼近

根据二项式扩展模型逼近函数的特性，可将式(10)运算后变为

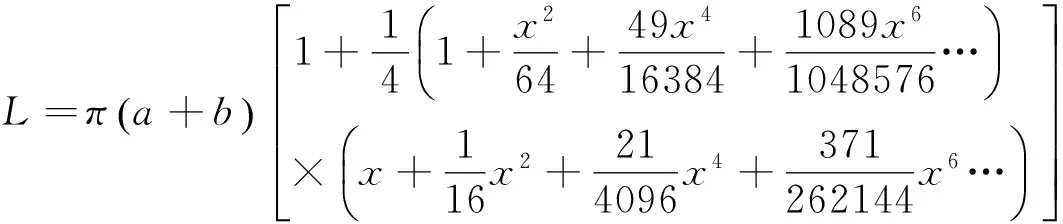
(15)

进一步运算可得到以下有理分式(不同于Padé逼近中的有理分式)

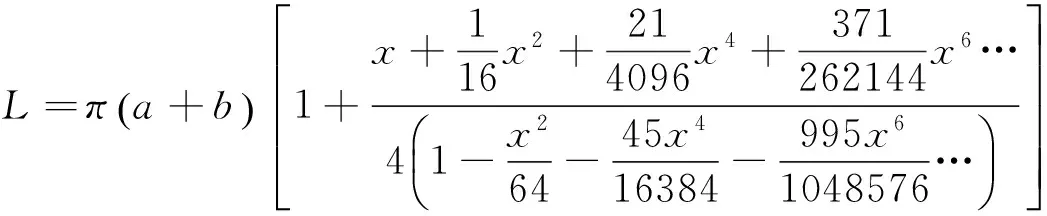
(16)

采用前述方法对式(16)的分子、分母分别逼近可得到第四个近似公式，即

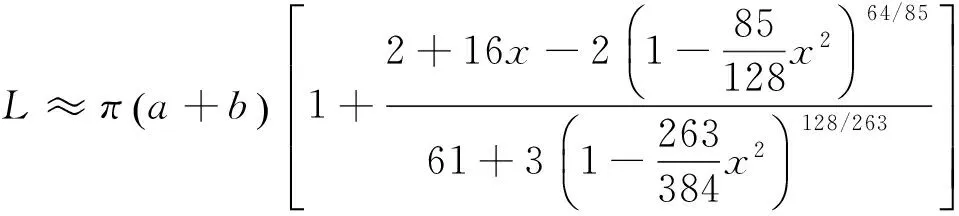
(17)

3.2.4 不同方法组合逼近

不同的逼近方法可以组合应用.比如，将式(16)进一步运算可变为

(18)

用相同的方法可得到第五个近似计算公式

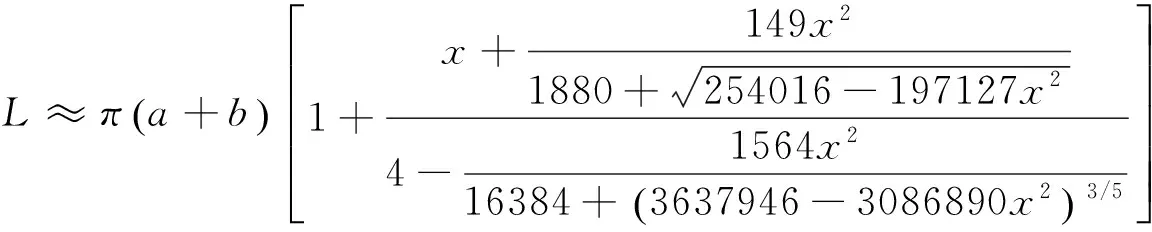
(19)

注 式(19)中的指数3/5为化简近似值.

上述例举了应用二项式扩展模型获取椭圆周长公式的几个具体方法和实例，通过各种逼近方法的组合应用还可得到更多的近似公式，这里不再赘述.

3.3 误差分析

上述式(9)，(12)，(14)，(17)和(19)五个椭圆周长近似公式，精度如何？不妨通过实例加以说明.

假设有4个椭圆，长半轴a值均为500，离心率e分别为0.28，0.6，0.8，0.96，则短半轴b值分别为480，400，300，140.据此，可分别计算不同的x值，并按照公式(1)取足够精度要求的级数项来计算椭圆周长.假设按公式(1)计算的结果为椭圆周长的真值，将对应的x代入上述5个近似公式，便可计算不同椭圆周长的近似值；真值减去近似值的差与真值相比，便可得到相对误差，据此即可判断近似公式的精确度.

为便于分析，将上述设定的数据和计算值列于表1.

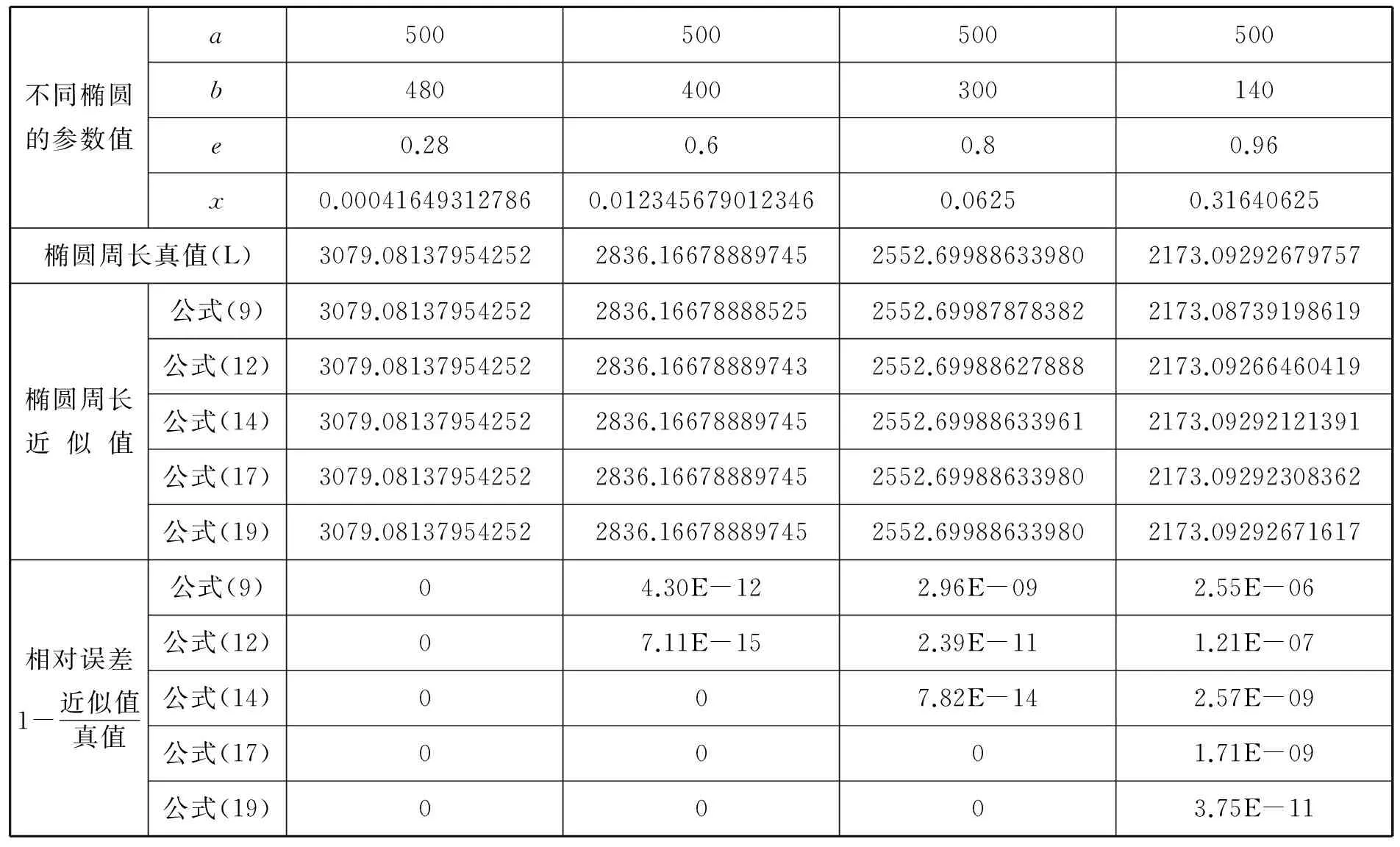
表1 椭圆周长近似计算公式误差对比表

表1应用5个近似公式，分别计算了4个不同参数的椭圆周长的近似值和相对误差.从误差情况看，同一公式计算不同离心率的椭圆周长，离心率越小，精度越高；而5个不同的近似公式用于计算相同离心率的椭圆周长，公式精度依次有所提高.精度最高的是式(19)，离心率小于0.8时，精度至少达到了15位以上有效数值，这一精度在天文计算中也是可以应用的.

4 结 语

本文提出了一个二项式扩展模型，用于逼近椭圆周长，得到了五个近似计算公式.逼近过程运算简单，实证分析精度较高，说明应用这一模型逼近椭圆周长是非常实用的.二项式扩展模型是否能够用于逼近其他函数？如果答案肯定，则必将能够丰富函数逼近理论和扩展函数逼近方法，期待广大学者研究论证.

[1] 周祖逵.椭圆周长近似公式[J] .数学通报,1995，34(6)，45-47.

[2] Roger W, Barnard, Kent Pearce, Kendall C, Richards. A Monotonicity Property Involving 3F2 and Comparisons of the Classical Approximations of Elliptical Arc Length[J]. SIAM J. Math. Anal., 2000 , 32, (2):403-419.

[3] 王仁宏.数值逼近[M].北京：高等教育出版社,1999： 17-26.

One Binomial Expansion Model and its Application in Approximation for Perimeter of an Ellipse

FENGYou-kuan

(Inner Mongolia Human Resources and Social Security Department, Hohhot 010055, China)

We first propose the 3 parameters binomial approximating model for the series expansion of ellipse perimeter which can’t be refined calculated by elementary function; Using this model, we discusses the basic method for approximating the ellipse perimeter, and obtain 5 compacted approximate formula; We take instance analysis to prove the accuracy and practicability of this model.

binomial; expansion model; function approximation; the perimeter of an ellipse

2015-12-18； [修改日期] 2016-08-22

冯有宽(1960-),男，学士，从事养老保险研究.Email:fengyoukuan@126.com

O174.41

C

1672-1454(2016)05-0116-05