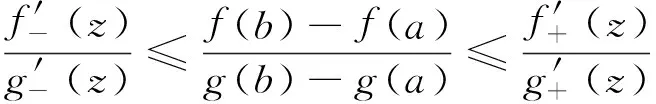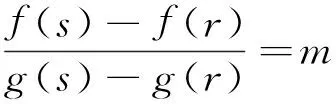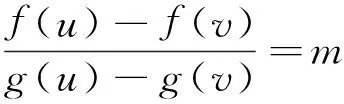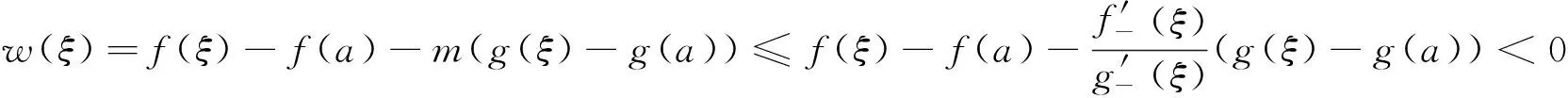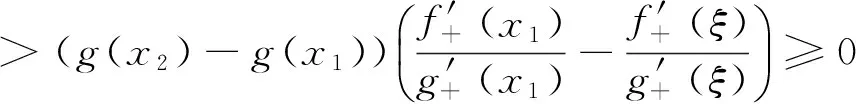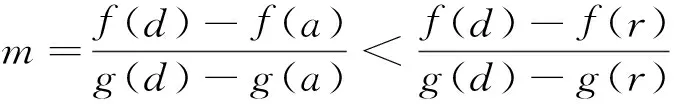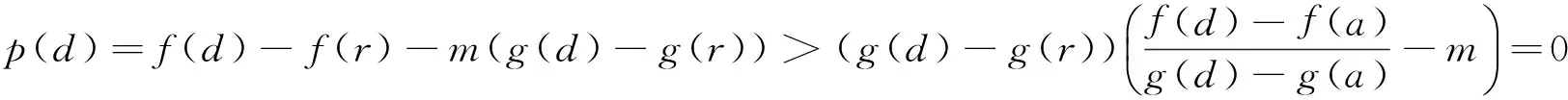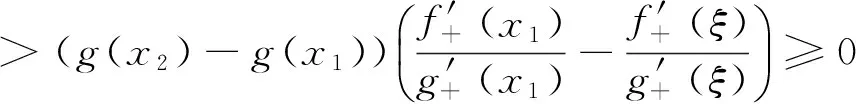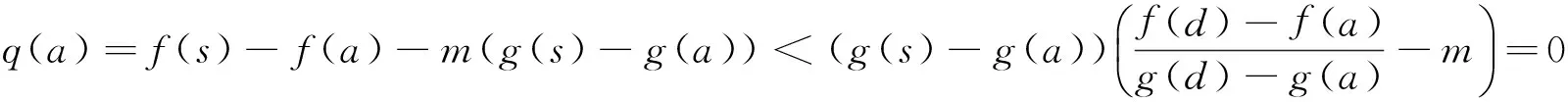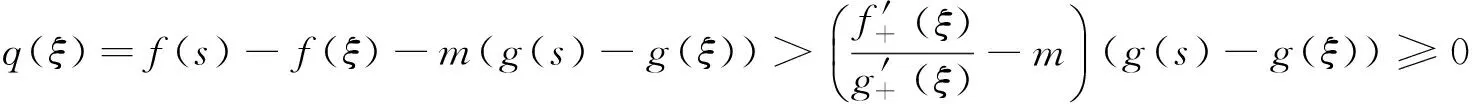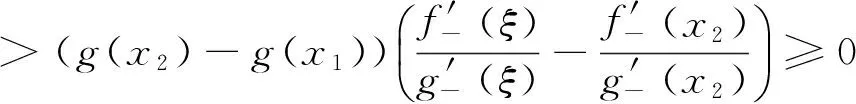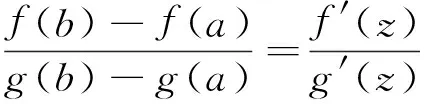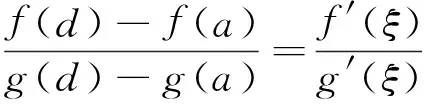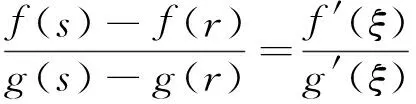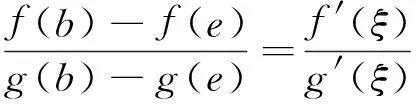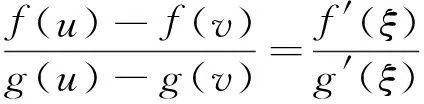再论Cauchy微分中值定理的逆问题
王良成,马秀芬,杨明硕
(重庆师范大学涉外商贸学院,重庆401520)
再论Cauchy微分中值定理的逆问题
王良成,马秀芬,杨明硕
(重庆师范大学涉外商贸学院,重庆401520)
文[1]给出了“Cauchy微分中值定理”中值点唯一的条件,并得到了其逆定理的较弱表述.继续文[1]的工作,利用闭区间上连续函数的性质及函数的单调性,解决了其逆定理中端点的唯一性.
Cauchy微分中值定理; 严格单调性; 左右导数; 导数; 逆问题
1 引 言
本文均假定f(t)与g(t)在[a,b]上连续, g(t)在t∈(a,b)处左右导数均存在且恒正(即g(t)在[a,b]上严格递增(参见[2]).对∀c∈(a,b),定义函数
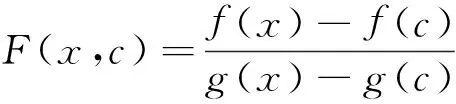
文[1]以较弱形式统一了“Cauchy微分中值定理”的逆问题,得到如下定理.
定理A 对∀c∈(a,b),若函数F(x,c)关于x在[a,c)∪(c,b]上严格递增,则存在r,s∈[a,b],r 若函数F(x,c)关于x在[a,c)∪(c,b]上严格递减,则上式反向成立. 若函数F(x,c)关于x在[a,c)∪(c,b]上严格单调, f′(c)与g′(c)存在且g′(c)恒正,则存在r,s∈[a,b],r 本文的目的是解决上述定理中r与s的唯一性问题.为了解决本文的问题还须文[2]中如下定理. 定理B 对∀c∈(a,b),若函数F(x,c)关于x在[a,c)∪(c,b]上严格递增,则f′-(c)与f′+(c)均存在,且有如下三个不等式 1. 对a≤x1 (1.1) 2. 对∀r,s∈(a,b),r (1.2) 3. 对∀x∈[a,b], x≠c, 则有 (1.3) 若F(x,c)关于x在[a,c)∪(c,b]上严格递减,则f′-(c)与f′+(c)均存在且上述三类不等式反向成立. 定理2.1 对∀c∈(a,b),若函数F(x,c)关于x在[a,c)∪(c,b]上严格递增, 则有如下三个结果. (i) 存在唯一的z∈(a,b)使得 (2.1) ① 存在唯一的d∈(ξ,b)使得 (2.2) 反之对上述的d,只有a才能使上式成立. ② 对∀r∈(a,ξ)及上述的d,则存在唯一的s∈(ξ,d),使得 (2.3) 反之对上述的d及∀s∈(ξ,d),则存在唯一的r∈(a,ξ)才能使上式成立. ① 存在唯一的e∈(a,ξ)使得 (2.4) 反之对上述的e,只有b才能使上式成立. ② 对∀u∈(ξ,b)及上述的e,则存在唯一的v∈(e,ξ)使得 (2.5) 反之对上述的e及∀v∈(e,ξ),则存在唯一的u∈(ξ,b)才能使上式成立. 当F(x,c)关于x在[a,c)∪(c,b]上严格递减时,则(i)-(iii)中的不等式均反向. 证 (i) (2.1)式及唯一的z∈(a,b)是文[1]中定理3的直接结果. (ii) ① 设w(x)=f(x)-f(a)-m(g(x)-g(a)), 则w(x)在[ξ,b]上连续.由已知及 (1.3)式有 由 (2.1)式, 已知及(1.2)式有 由连续函数零点定理知,存在d∈(ξ,b)使得 f(d)-f(a)-m(g(d)-g(a))=w(d)=0, 即(2.2)式成立. 对∀x1,x2∈[ξ,b] , x1 w(x2)-w(x1) =f(x2)-f(x1)-m(g(x2)-g(x1)) 即w(x)在[ξ,b]上严格单调递增.则(2.2)式中的d是唯一的. 对∀r∈(a,ξ),则a 即对于上述的d,只有a才能使(2.2)式成立. ② 对∀r∈(a,ξ),设p(x)=f(x)-f(r)-m(g(x)-g(r)),则p(x)在[ξ,d]上连续.由已知及 (1.3)式有 由a 由零点定理知,存在s∈(ξ,d)使得f(s)-f(r)-m(g(s)-g(r))=p(s)=0,即(2.3)式成立. 对∀x1,x2∈[ξ,d] , x1 p(x2)-p(x1) =f(x2)-f(x1)-m(g(x2)-g(x1)) 即p(x)在[ξ,d]上严格单调递增.则(2.3)式中的s是唯一的. 反之对∀s∈(ξ,d),设q(x)=f(s)-f(x)-m(g(s)-g(x)),则q(x)在[a,ξ]上连续.由a 由已知及(1.3) 式有 由零点定理知, 存在r∈(a,ξ)使得f(s)-f(r)-m(g(s)-g(r))=q(r)=0,即(2.3)成立. 对∀x1,x2∈[a,ξ] , x1 q(x2)-q(x1) =m(g(x2)-g(x1))-(f(x2)-f(x1)) 即q(x)在[a,ξ]上严格单调递增.则(2.3)式中的r是唯一的. (iii) 设k(x)=f(b)-f(x)-m(g(b)-g(x)), 仿照(ii)中①的证法,可证得(2.4)式; 对∀u∈(ξ,b),设l(x)=f(u)-f(x)-m(g(u)-g(x)), 再仿照(ii)中②的前半部分的证法,可证得:存在唯一的v∈(e,ξ)使得(2.5)式成立; 反之对∀v∈(e,ξ),设j(x)=f(x)-f(v)-m(g(x)-g(v)), 仍仿照(ii)中②的后半部分的证法,可证得:存在唯一的u∈(ξ,b)才能使(2.5)式成立. 由定理2.1直接可得如下定理. 定理2.2 对∀c∈(a,b),若函数F(x,c)关于x在[a,c)∪(c,b]上严格单调,f′(c)与g′(c)存在且g′(c)恒正,则有如下三个结果 (i) 存在唯一的z∈(a,b)使得 (ii) 对∀ξ∈(a,z),则存在唯一的d∈(ξ,b)使得 反之对上述的d,只有a才能使上式成立.且对∀r∈(a,ξ),则存在唯一的s∈(ξ,d),使得 反之对∀s∈(ξ,d),则存在唯一的r∈(a,ξ)才能使上式成立. (iii) 对∀ξ∈(z,b),则存在唯一的e∈(a,ξ)使得 反之对上述的e,只有b才能使上式成立.且对∀u∈(ξ,b),则存在唯一的v∈(e,ξ)使得 反之对∀v∈(e,ξ),则存在唯一u∈(ξ,b)才能使上式成立. 注1 当g(x)=x时,本文的定理A、定理2.1与定理2.2的结果变为文[3]中主要定理的相应结果. 注2 当g(x)在[a,b]上严格单调递减时,仍有与本文定理相应的结果. [1] 王良成,等.与Cauchy微分中值定理相关的几个问题[J]. 高等数学研究, 2013,16(5):9-11. [2] 王良成.凸函数及其不等式[M]. 成都:四川大学出版社, 2001. [3] 王良成,等.关于Lagrange微分中值定理的逆问题[J]. 大学数学, 2012,28(5):140-143. Further Discuss Inverse Problem of Cauchy’s Differential Mid-VaIue Theorem WANGLiang-Cheng,MAXiu-fen,YANGMing-Shuo (Chongqing Normal University, Foreign Trade And Business College, Chongqing 401519, China) In the paper [1], the condition of unique mid-value point for " Cauchy’s differential mid-value theorem " is given, and its the inverse theorem of weak expression is obtained. In this paper, we continue to the work of the paper [1]. By the properties of continuous functions on closed interval and monotonicity of function, we solve the uniqueness of end-point for its the inverse theorem. Cauchy’s differential mid-value theorem; strictly monotonicity; left and right derivative;derivative; inverse problem 2015-06-10; [修改日期] 2016-06-26 重庆师范大学涉外商贸学院重点科研项目(KY2015001) 王良成(1949-),男,教授,从事凸分析研究,Email: wlc@cqut.edu.cn O178 C 1672-1454(2016)05-0101-04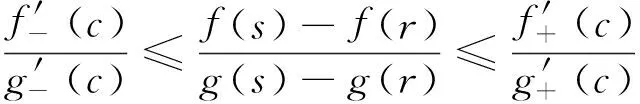
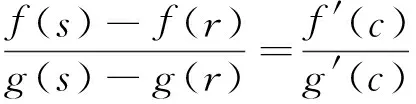
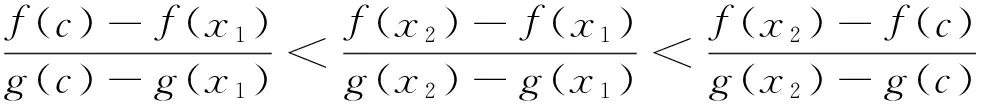
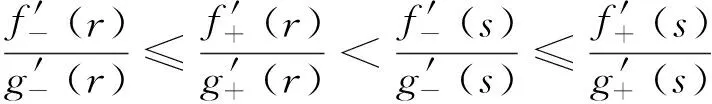

2 主要结果