高等数学成绩影响因素分析——以沈阳师范大学为例

杨淑辉, 孔朝莉

(1.沈阳师范大学计算机与数学基础教学部，沈阳110034； 2. 三亚学院理工学院，海南三亚572022)



高等数学成绩影响因素分析
——以沈阳师范大学为例

杨淑辉1, 孔朝莉2

(1.沈阳师范大学计算机与数学基础教学部，沈阳110034； 2. 三亚学院理工学院，海南三亚572022)

在本科一年级理工类学生中进行问卷调查，获取高等数学成绩影响因素的样本数据.利用因子分析测量问卷的结构效度，并实现对影响成绩各因素的正交化变换，为进一步的最优尺度回归提供筛选变量的依据.采用最优尺度回归分析来探索高等数学成绩的影响因素，结合教学实际，对各因素进行有针对性地分析，提出改进教学效果的建议和措施.

最优尺度回归； 因子分析； 高等数学成绩； 调查问卷

1 引 言

本文所提及的“高等数学”，并非与初等数学对应的广义高等数学，而是专指理工类学生学习的一门课程，其主体内容为“微积分”.

近几年来，高等数学教学模式多样，教学方法不断改进，学界对于教学模式的应用研究探讨较多，但是对其有效性的研究相对较少[1].本文从沈阳师范大学2015级理工类学生中，抽取翻转课堂、传统模式等不同教学模式的教学班进行问卷调查，结合问卷调查获得的数据，利用因子分析测量问卷的结构效度.采用最优尺度回归分析教学模式对学生高等数学成绩的影响，对影响学生高等数学成绩的各种因素的重要程度进行排序，对教学改革实践经验进行总结，从而明确高等数学课程教学改革的主要方向.

2 问卷设计与因子分析

问卷设计的问题主要围绕影响学生学习成绩的各种因素，影响因素的选择参考了学界已有的研究成果[2-4].

此次调查共计发放问卷254份，实际回收有效问卷222份，其中翻转课堂模式有效问卷63份，常规教学模式有效问卷159份.

表1列出的17个影响因素，水平类型不尽相同，故不做问卷的内在信度检验.利用SPSS20.0，对相关系数矩阵进行因子分析，检验问卷的效度.采用KMO检验和巴特利特球体检验，KMO检验系数为0.598>0.5，巴特利特球体检验的显著性远远小于0.05，表明问卷有结构效度，可以进行因子分析.利用主成分法提取公因子，采用最大方差法进行因子旋转，提取11个公因子，累积贡献率达到82.024%.以因子载荷大于0.4为标准，第1公因子在生源地、高考数学成绩和教学模式上载荷较大；第2公因子在学习数学的态度、高等数学学习上花费功夫和学习能力上载荷较大；第3公因子在对教师的认可上载荷较大(基础)；第4公因子在学习数学的动力来源、学习目的来源上载荷较大；第5公因子在外界对自身数学学习影响和对自身数学学习影响最大的因素上载荷较大；第6公因子在提高成绩的有利方案上载荷较大；第7公因子在民族上载荷较大；第8公因子在对大学生活的定位上载荷较大；第9公因子在性别上载荷较大；第10公因子在年龄上载荷较大；第11公因子在对所学专业了解程度上载荷较大.具体载荷见表2.成分得分系数矩阵近似单位阵，完成了各因素的正交化处理.为进一步的最优尺度回归提供筛选变量的依据.

表1 影响因素及水平表

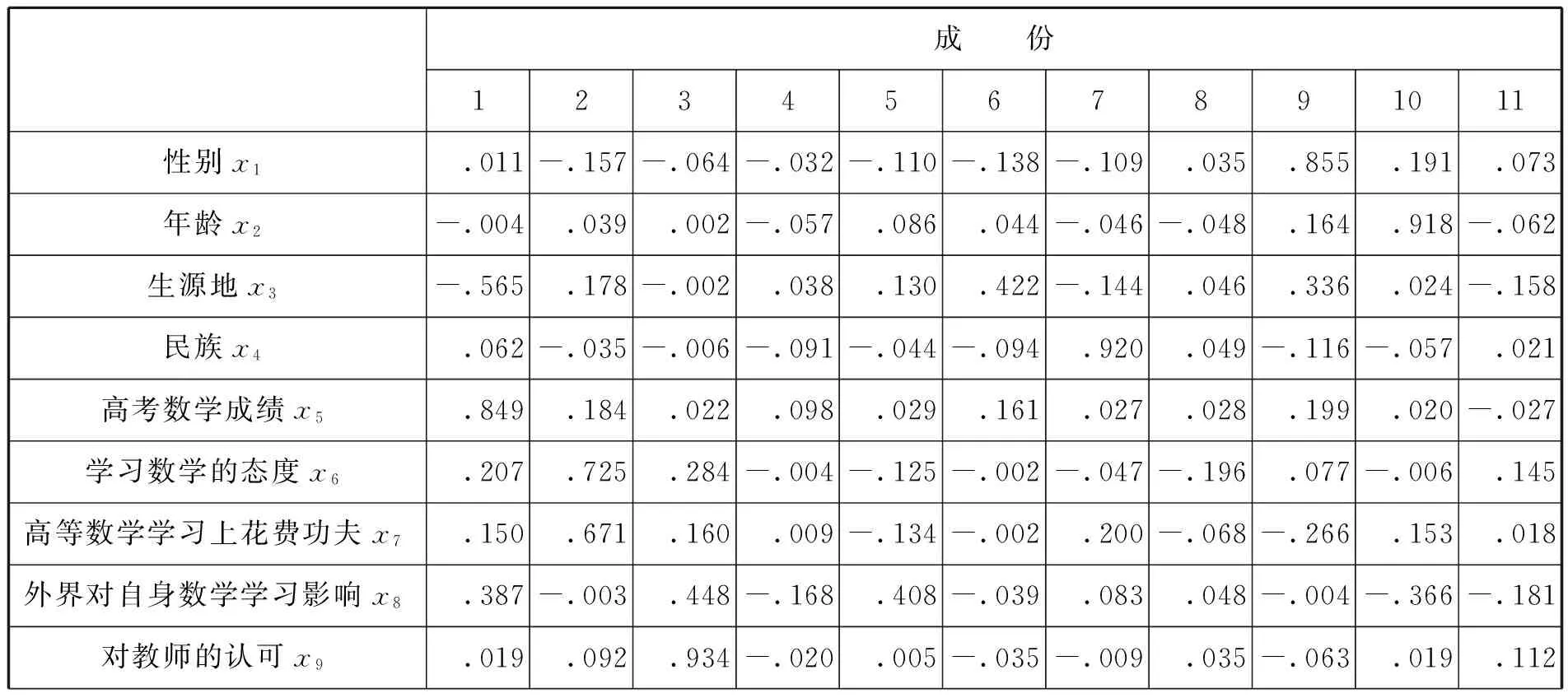
表2 旋转成份矩阵

续表2

3 最优尺度回归模型

为了探索各因素对学生学习成绩的影响程度，找出问题的主要根源，采用最优尺度回归分析来进一步对分类变量进行分析.最优尺度回归是标准回归方法的扩展，它按照比例换算名义变量、有序变量及数值型变量，使用定量化的方法反映各种变量的属性，并利用非线性转换求解最佳的回归方程.

将大学数学平均成绩作为因变量Y，问卷涉及到的17个因素作为自变量，利用SPSS20.0进行最优尺度回归，发现有的参数检验无法通过.结合因子分析的结果，将同一类公因子中的最不显著变量剔除，最终剩余9个显著的自变量.对各自变量作为无序变量进行分析，再根据量化转换图进行修正，有序变量为：教学模式、性别和学习数学的态度；因变量Y为数值型，进行离散化处理，采用正态分组处理；其它变量为无序变量；自变量采用排秩法进行离散化处理.最终得到回归结果见表3-表4.拟合优度R2=0.601，模型在10%显著性水平下具有统计学意义.标准化最优尺度回归模型：

+0.113x16-3.313x17.

容差都不是很小，自变量之间不存在明显的线性关系，每个自变量不能被其它变量解释变异均在0.83以上.重要性是根据标准化系数和相关系数计算出的自变量在模型中的重要程度百分比，所有自变量的重要性加起来等于100%，数值越大表明该变量对因变量的预测越重要.从表4可以看出各自变量对因变量的重要性从大到小依次是：教学模式、学习数学的态度、学习能力、学习数学的动力来源、性别、对大学生活的定位、提高成绩的有利方案、学习目的来源、对自身数学学习影响最大的因素.

从量化转换图(图1)及回归系数分析各变量水平的量化评分情况：

教学模式量化转换评分情况：普通课堂评分为0.63，翻转课堂评分为-1.59，结合回归系数，表明翻转课堂教学模式对学生成绩影响是正向的；

学习数学的态度中四个水平评分呈递增趋势：恐惧(负)、一般(负)、比较感兴趣、非常感兴趣；

学习能力评分由高到低分别是:较好地完成学习任务、很好地完成任务同时自学其它、不会学习(负)、能完成基本任务(负)；

学习数学动力评分由高到低分别是: 家庭、专业所需、自身爱好、无动力；

性别变量被重新评分，男生转换后被量化评分为-0.66，女生被量化评分为1.51，表明男生成绩比女生要差，女生为正，男生为负，间距不再是1；

大学生活中最重要要素评分由高到低分别是: 学习、社团及学生会工作、社会实践 、其它(负)；

提高成绩的有利方案评分由高到低分别是:教材内容的调整、教师教学水平的提高、考核方式的调整、自身的努力(负)；

学习目的来源评分由高到低分别是：无目的、个人兴趣爱好、完成家长要求、其它、为将来工作打基础(负)；

数学学习影响最大因素评分由高到低分别是: 其它、自身基础、个人兴趣、学习氛围、教师(负).

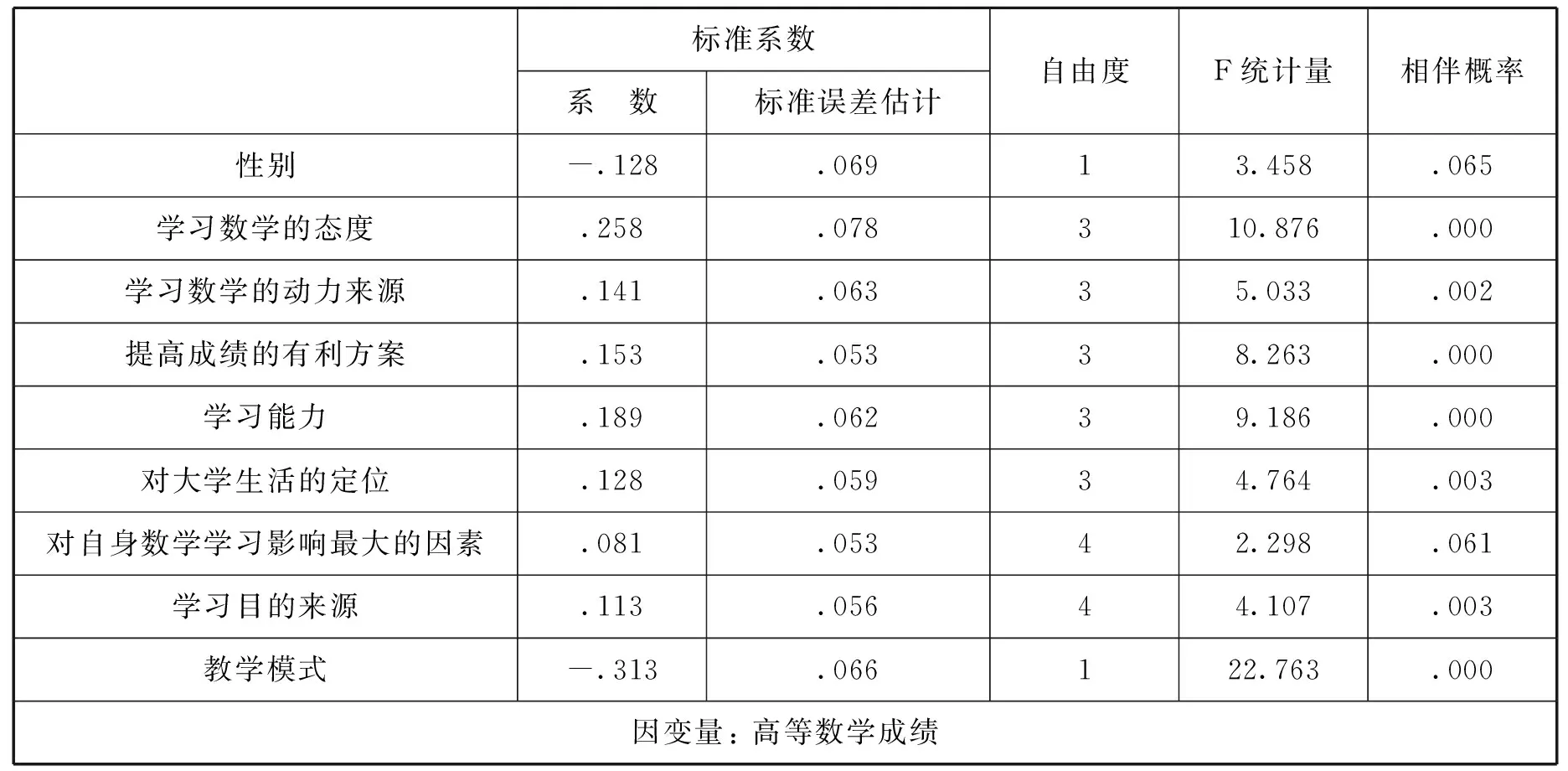
表3 回归系数

表4 相关性和容差

图1 自变量的量化转换图

4 结论与对策建议

通过对问卷结果的最优尺度回归分析，剔除了17个影响因素中8个不显著影响因素，保留9个显著影响因子.数据显示，对此次调查对象的高等数学成绩影响程度从大到小依次为：学习数学的态度、教学模式、学习能力、学习数学的动力来源、性别、对大学生活的定位、提高成绩的有利方案、学习目的来源、对自身数学学习影响最大的因素.

4.1 教学模式与学习态度

9个显著性影响因子中，教学模式的重要性为0.339，学习态度的重要性为0.270，教学模式重要性更大，这两个公因子的重要性占比60.9%.

在有效问卷中，对于学习数学的态度，选择比较感兴趣的占47.1%，选择兴趣一般的占35.6%，选择非常感兴趣的占13.6%，选择恐惧的占3.7%.

不同教学模式的学生群体对高等数学的感兴趣程度不一样.表5表明，实施翻转课堂的学生学习兴趣更高，成绩也更理想.教学模式和学习态度相辅相成，成为影响高等数学成绩的重要因素.参与翻转课堂学生的高等数学试卷成绩平均分为82.5分，普通班学生的高等数学试卷成绩平均分为66.9分(两种教学模式采用同一张试卷，试卷成绩有对比性，总评成绩构成方式不同).翻转课堂教学模式班是辽宁省“大学生在线学习跨校修读学分”试点教学班，课程教学由跨校网络课程教学和本校面授课堂教学两部分构成.课程结业成绩由平时成绩、网络课程成绩、期末试卷成绩三部分构成.课程学习包括“课下和课上”学习.课下学习包括：教材学习、网络课程学习、资料学习、讨论释疑.课上学习包括：知识回顾、知识拓展、自主学习问题反馈讨论、巩固新知、综合练习、课后任务布置、讨论总结.学生5人划分为一个学习小组，每次课前教师会在群中公布导学教案和学习任务，指定一组学生在课上对学习任务进行讲解，教师实时点评，学生讨论.在这种教学模式下，学生必须花更多的时间完成网络课程和面授课程的教学任务.常规模式教学班，采用教师一言堂，学生被动学习模式.

表5 学习态度对比

两种教学模式下学生成绩差异明显，导致这种差异的因素，除了教学模式因素，也不排除其它导致学生成绩差异较大的因素.如：生源选择、师资配备、教学班人数、学生管理等.翻转课堂教学模式班在资源占有上有所倾斜，生源质量较高，教学班的人数少于传统教学班，且在教学管理上更为严格.

图2 高等数学成绩和高考数学成绩散点图

一些研究结论[5-6]认为高等数学成绩和高考数学成绩正相关，但此次调查二者的Pearson相关系数为0.266，从图2也可以看出，两类数学成绩分布无明显的规律性，不存在明显的线性关系，表明翻转课堂班与普通班学生的数学基础在统计学上无显著差异.可以认为教学模式的差异是导致学生成绩差异的主要原因.

据此次调查结果，在教学资源和管理对翻转课堂教学模式教学班有优待的条件下，翻转课堂教学模式和积极的学习态度对学生成绩的影响是正向的.但在同等教学条件下，教学模式和学习态度对学习成绩的影响是否为正向还有待于进一步验证.

4.2 学习能力与学习动力

调查结果表明，学习能力对高等数学成绩的重要性为0.138，学习动力的重要性为0.076.在对自身学习能力的评价上，51.8%的学生认为能完成基本任务，40.8%认为能较好地完成任务，5.8%的学生认为自己不会学习,1.6%的学生不能很好地完成任务.对于学习动力，选择专业所需的学生占71.2%，选择动力来自自身爱好的学生占21.4%，选择动力来自家庭和无动力的各占3.7%.

根据调查结果，给出的对策建议，将学习能力培养应放在与传授知识同等重要的地位.学生的学习动力一般来源于生活实践中对高等数学内容的需求及专业课程对高等数学知识的需要.优化课程结构，加强高等数学课程与专业课程的衔接，指导学生参与数学建模等学科竞赛，在实践中即能提升能力，也能为学生提供学习的动力.

4.3 性别与对大学生活的定位

性别对高等数学成绩的重要性为0.071，对大学生活的定位的重要性为0.069.

从实际数据统计结果来看，女生高等数学平均成绩73.9，男生平均成绩65.2，女生平均分比男生高8.7分.调查中女生占69.6%，男生占30.4%.

关于大学生活，调查对象中选择学习的占38.7% ，选择社会实践的占39.8%，选择人际关系的占13.1%，选择其它的占8.4%，社团及学生会工作无人选.

从教学实际来看，女生学习比男生更认真，到课情况和作业完成情况更强于男生，教师应加强对男生的管理，多进行有效沟通.管理部门应建立有效的实时监控机制，制定行之有效的管理措施，督促学生学习.调查问卷结果显示，大学生认为大学生活中最重要的应该是学习和社会实践，实际上这两者并不冲突.应用型人才培养计划就是学以致用，实践出真知.高等数学是从生活中抽象出来的学问，应用高等数学知识解决实际问题，增强实践能力.

4.4 影响高等数学成绩的其它因素

提高成绩的有利方案对高等数学成绩的重要性为0.022，学习目的重要性为0.009.

对于怎样才能提高高等数学成绩，选择自身努力的占85.3%，选择考核方式调整的占5.8%，选择教师教学水平提高的占5.2%，选择教材内容调整的占3.7%.

对于学习高等数学的目的，选择无目的占1.6%，选择完成家长要求的占1%，选择为将来工作打基础的占75.4% ，选择个人兴趣爱好的占8.9% ，选择其它的占13.1%.

自身数学学习影响最大的因素的重要性为0.008.选择个人兴趣的占57.6%，选择学习氛围的占19.9%，选择自身基础的占8.4%，选择教师的占7.9% ，选择其他的占6.3%.

从影响高等数学成绩的后三种因素分析，学生学习高等数学的主要目地是为将来工作打基础，而将来工作的专业知识主要来源于专业课程，因此高等数学课程应定位于服务专业课程.这就要求教师在知识背景介绍、例题选择、案例设计、教材编写等环节与专业课程有效对接[7].

4.5 对策建议

根据实际课堂教学改革实践和此次的调查结果，提出未来高等数学课程教学改革的具体建议：

第一，明确高等数学的课程观和课程目标是：通过课程学习，辅助学生的专业课程学习；锻炼用数学思维去解决实际问题的能力，增进对数学的理解和兴趣；培养学生应用数学工具分析问题、解决问题的能力，使学生能适应社会经济生活的需要.对高等数学课程合理定位，以适应大多数学生对大学生活的定位，调动学生的学习积极性.

第二，根据专业需求优化课程结构，分模块、分层次教学[8].为不同需求的学生提供不同的学习内容，才能给学习动力不同的学生提供相应的学习动力.

第三，根据高等数学课程的学科特点和不同教学内容的需求，采用翻转课堂教学模式、师生互动对话教学模式、信息技术支撑教学模式等多种教学模式混合教学.交叉使用课堂讲授教学、网络课程教学、微课、慕课、线上线下结合等多种教学组织形式，由传统的讲授教学拓展到“自主式、讨论式、研究式”的教学模式[9].

此次进行跨校修学分翻转课堂教学班与常规班比较，反映出来的积极方面有：整学期出勤满勤率达到99%；教师布置作业完成效果好；课上气氛活跃，参与度高；学生的表达能力和自主学习能力都有所提升；随堂测试结果显示，知识掌握牢固.

但是高等数学课程在进行网络学习，翻转课教学模式时常会遇到下列困难：教学环境问题，网络课程教学平台还不够稳定，经常出现页面崩溃，登录失败等现象，在登录高峰期视频播放页面卡顿，不流畅，浪费在非学习上的时间太多.有些学生没有方便的学习设备及网络环境，不能有效利用闲散时间，随时随地的进行网络学习；课程内容较多，网络课程资源建设内容还不够细致；网络作业和网络测试难以实现，数学的学科特点是公式、符号、图形较多，网络技术还不能灵活支持上述输入要求，学生无法在网络上灵活处理作业，网络测试也不能有效实现；《高等数学》课程难度较大，学生自主学习很难深入，课堂讨论抓不住重点，不够活跃，需要老师明确的问题导引；师资力量薄弱，没能及时对学生的网络课程学习进行及时反馈.鉴于此，提出第四点建议.

第四，为学生创设方便的网络环境和网络设备；开发具有数学学科特点网络题库，供学生经常性的自我检测，同时也减轻教师的负担；建设与专业教学相衔接的教学方案，加强导学案建设，对学生的自主学习过程进行有效导引，提高自主学习的有效性；建设与专业对接的教学案例，将高等数学的教学与专业紧密联系.提高学生学习数学的积极性，也提升教师和学生的建模能力；加强网络课程反馈，提高学生的学习积极性；积极鼓励学生参加数学竞赛、数学建模大赛、大学生创新创业项目等，在实践环节应用所学；尽可能在每一节课对学生的自主学习成果进行考核和评价，督促学生进行自主学习；教师加强学习，深入了解学生的专业课程，使高等数学课程与专业课程更好的衔接.通过课上、课下及互联网的多种沟通方式加强与学生的沟通和交流.

5 结 论

在国内，关于大学数学成绩影响因素的研究[10]，一般仅找出了主要的影响因素，未体现出各因素的影响程度，本文通过对来自学生的真实数据的分析，利用最优尺度回归模型，对调查群体影响学生数学成绩各要素的重要性进行了排序，对学生学习的现状有了进一步认识.尤其是对翻转课堂教学模式的实践经验进行了总结，对教学模式有效性的定量分析做出了有益尝试.下一步希望能对教学模式与学习积极性之间的关系，同等条件下翻转课堂教学模式与常规教学模式的有效性进行实践研究.

[1] Christa Lee Quint. A study of the efficacy of the flipped classroom model in a university mathematics class [D]. New York：Teachers College, Columbia University，20 May 2015.

[2] Milne, L. Bridging mathematics students: Attitudes, autonomous leaming behaviours, and problem solving.In B Southwell, B Perry & K Owens.(eds),Proceedings of the Fifteenth Annual Conference Mathematics Education Research Group of Australasia(MERGA)UNWS Conference Centre[C]. Richmond:The Mathematics Education Group of Australasia, 1992:382-389.

[3] Dungan,J F, Thurlow, G R. Students.attitudes to mathematics: A review of the literature[J]. The Australian Mathematics Teacher,1989,45(3):8-11.

[4] 杨云苏，王礼胜，罗润生.影响大学生数学成绩的三因素研究[J].数学教育学报，2008，17(6)：56-59.

[5] 曾艳,段春生,向丽.影响民航大学生数学学习成绩的因素[J].内江师范学院学报，2011,26(4)：79-81.

[6] 方晓伟. 影响学生大学数学成绩因素的统计分析[J]. 高等函授学报(自然科学版)，2010,23(5)：49-51.

[7] 杨淑辉,李营,孔朝莉.HPM视角下的微积分绪论课[J].沈阳师范大学学报(社会科学版)，2009,27(2)：161-163

[8] 张香云，王家军，贺志民. 高等数学课程分层次教学理念的思考和举措[J].大学数学，2014，30(1): 56-59.

[9] 张文彤.分析教学法初探[J]. 大学数学，2014，30(1): 121-123.

[10] 梁好翠,黄岳俊.教学自我监控及学习动机对数学学习成绩影响机理的研究[J].数学教育学报，2011,20(1)：58-60.

Analysis of Factors Influence Student’s Achievement in Higher Mathematics——Taking Shenyang Normal University as an Example

YANGShu-hui1，KONGZhao-li2

(1.Department of Computer and Mathematics Teaching, Shenyang Normal University,Shenyang 110034,China;2.Science and Technology Department，Sanya College，Sanya Hainan 572022，China)

The article took samples by survey on the freshman. Firstly, it tested the construct validity by factor analysis and realized orthogonalization conversion of factors that influence student’s achievement in mathematical courses to provide reference while choosing variables for the optimal scaling analysis. By optimal scaling analysis, the article endeavored to find out those main factors that affected student’s achievement in mathematical courses. Hanging together the teaching status the article analyzed where those main factors come from and put forward some corresponding suggestions to improve classroom teaching and students management.

optimal scaling; factor analysis; higher mathematics achievement;survey

2016-5-18； [修改日期] 2016-06-24

辽宁省本科教改立项一般项目(2016464)；辽宁省本科教改立项优质教育资源共建共享项目(2016110)；海南省自然科学基金资助项目(20151007)

杨淑辉(1978-)，女，硕士，副教授，从事数学史与数学教育研究.Email:ysh9167@163.com

G645; O213.9; F2

B

1672-1454(2016)05-0037-08