2015年高考北京理综卷第24题的深度解析与思考
张 适
(北京市育英学校 北京 100036)
2015年高考北京理综卷第24题的深度解析与思考
张 适
(北京市育英学校 北京 100036)
主要通过对2015年高考北京理综卷第24题的分析,进而对本题重点考查的相关核心概念作了拓展探讨,指出了平时物理教学中应注意的问题.
北京高考 电源 电动势 内阻
2015年高考北京理综卷物理第24题以平行板光电转换装置为情境,将光电效应、匀强电场、电流、直流电源、闭合电路融合为一道题,突出考查学生对核心概念电动势、电流的多角度深刻理解.此题意境新颖,构思巧妙,综合性强,突出了对学生物理思想以及综合能力的考查,有较大的难度和区分度.
1 原题
真空中放置的平行金属板可以用作光电转换装置,如图1所示.光照前两板都不带电.以光照射A板,则板中的电子可能吸收光的能量而逸出.假设所有逸出的电子都垂直于A板向B板运动,忽略电子之间的相互作用.保持光照条件不变.a和b为接线柱.
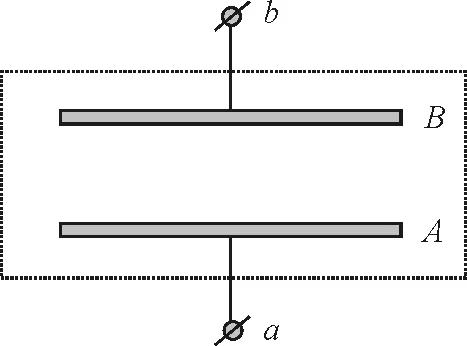
图1
已知单位时间内从A板逸出的电子数为N,电子逸出时的最大动能为Ekm.元电荷为e.
(1)求A板和B板之间的最大电势差Um,以及将a和b短接时回路中的电流I短.
(2)图示装置可看作直流电源,求其电动势E和内阻r.
(3)在a和b之间连接一个外电阻时,该电阻两端的电压为U.外电阻上消耗的电功率设为P;单位时间内到达B板的电子,在从A板运动到B板的过程中损失的动能之和设为ΔEk.请推导证明:P=ΔEk.
(注意:解题过程中需要用到、但题目没有给出的物理量,要在解题中做必要的说明)
2 解析
(1)由动能定理得Ekm=eUm,可得
短路时所有逸出电子都到达B板,故短路电流
I短=Ne
(2)电源的电动势等于断路时的路端电压,即上面求出的Um,所以
电源内阻为
(3)外电阻两端的电压为U,则电源两端的电压也是U.
由动能定理,一个电子经电源内部电场后损失的动能为
ΔEke=eU
设单位时间内有N′个电子到达B板,则损失的动能之和为
ΔEk=N′ΔEke=N′eU
根据电流的定义,此时电源内部的电流
I=N′e
此时流过外电阻的电流也是I=N′e,外电阻上消耗的电功率为
P=IU=N′eU
P=ΔEk
3 评析
本题设计有梯度,难度递进,第(1)、(2)问较为基础,从中可见命题者对试题难度值的控制,第(3)问体现高校选拔人才的需要.对一所普通中学202个考生进行统计,该题的难度系数是0.39,区分度为0.78.对该题每一步骤得分进行统计,其各分数分布人数如图2所示,说明试题各小问对各层次学生都有较好的区分度.对部分考生访谈时,普遍认为试题第(3)问难度很大,它与前两问联系不上,不知如何下手.不少教师对本题中的平行板等效电源模型存在疑问:电源工作时是通过什么非静电力做功的?当外电路闭合时,电源电动势和内阻是否发生变化?电源的内阻是如何产生的?学生更是一片茫然.因此,对该题有必要作深度探讨,给出较为全面的理解,同时感受该题的灵活之处与价值所在.
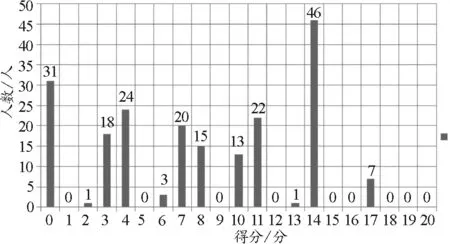
图2 人数分布图
4 深度解析
市场上的光电转换器(也称太阳能电池),是将相同的材料或两种不同的半导体材料做成PN结电池结构,当太阳光照射到PN结电池结构材料表面时,通过PN结将太阳能转换为电能.它的工作原理较为复杂,其电动势和内阻的性质也与普通的电池并不相同.可以认为命题者将光电转换器中的PN结简化成了光电效应实验中的两块平行金属板,变成了高中生熟悉的平行板电场模型;题目中的3条假设,实质上限定了该光电池的开路电压为一定值,是将光电池进一步理想化成学生熟悉的电池模型.
第(1)问考查了光电效应现象、光电效应的遏止电压和饱和光电流计算.这3项分别对应的是直流电源的工作原理、开路电压(电动势)和短路电流,也为第(2)问考查电源电动势和内阻的计算做铺垫.
第(2)问考查了电源两个特征量电源电动势和内阻的计算.电动势在数值上等于电源断路时电源两极间的电压;根据欧姆定律(或电阻的定义式),通过电源的短路电流来计算电源的内阻.
第(3)问从功能转换和能量守恒来进一步认识电源工作的实质.电源通过非静电力做功实现将其他能转化为电能,同时通过克服静电力做功来量度能量转化的多少.
5 拓展思考
5.1 对电源的非静电力的分析
从力的角度说,电源是通过非静电力来搬运电荷的装置.在不同的电源中,非静电力也是不同的.在化学电池(干电池、蓄电池)中,非静电力是一种与离子的溶解和沉积过程相联系的化学作用;在温差电源中,非静电力是一种与温度差和电子浓度差相联系的扩散作用;在一般发电机中,非静电力起源于磁场对运动电荷的作用,即洛伦兹力.光电转换器作为电源来说,是通过什么非静电力来搬运电荷的?根据光电效应现象知,当用大于极限频率的光照射A金属板时,一些电子俘获光子后,从金属表面逸出,以一定的初动能向B板运动,只要其初动能大于克服板间静电场力做功的数值,就可以到达B板,从而实现搬运电荷的作用.显然这里的非静电力只是发生在A板上的光电效应作用和从A板向B板运动的惯性,并非是真正意义上搬运电荷的“力”.
5.2 对电源能量的转化分析
从能的角度说,电源是将其他能转化为电能的装置.光电转换器作为电源,A金属板中的某些电子得到光子能量后动能突然增大,将光能转化为电子的动能.这些电子在逸出A金属板时,需要克服阻力做功和金属板的束缚作用做功而消耗一定的能量,才能从金属板中逸出成为光电子.由于这些电子得到能量时所处的位置不同,逸出时需要克服阻力所做的功不同,所以逸出金属表面时的初动能也不同,其中从金属表面直接逸出的电子初动能最大.这些光电子从垂直于A板方向逸出后,在A,B板间的运动情况与两板间的电压有关,即与外电路是否用电和消耗功率的大小有关,下面分情况讨论.
(1)若外电路短路时,A,B两板间电压为零,板间无电场,光电子从A板向B板匀速运动,动能不变.当光电子与B板相碰时,能量直接消耗在B板上.由于电路是闭合的,外电路并不消耗电能,电能只消耗在电源内部,也可以认为电源内阻消耗电能.
(2)若外电路断路时,外电路也不消耗电能,此时,A,B两板间电压最大为Um.由(1)问的解答可知,凡是从A板射出的光电子在电场中运动时,先向B板减速运动至速度为零,后反向加速返回A板,都不能到达B板,从A,B板间运动的全过程来说,这些电子克服静电力做的总功为零,其动能的变化量为零.这些电子反向运动直到与B板相碰,能量消耗在B板上,由于电路是断开的,所以并没有电流做功.
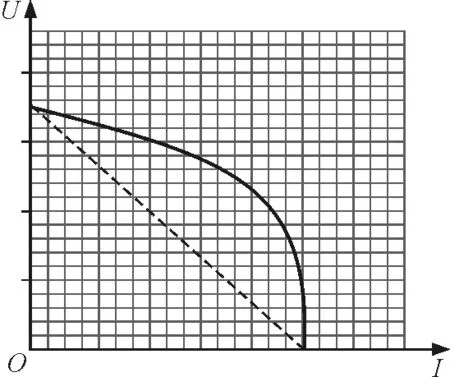
(3)若外电路接电阻时,外电路消耗的功率为P,由于A,B两板间有电压U( 5.3 对电源电动势的分析 由光电效应方程知,光电子的最大初动能为 Ekm=hν-Wc 代入 得两板开路电压(电动势) 显然,A板的金属材料给定后,逸出功Wc为定值,当用某一频率ν的光照射A板时,光电转换器的电动势E是确定的.果真如此吗?下面我们从能量的角度来推证. 这就意味着在A,B板间运动的每个光电子的最大初动能均为Ekm,这与实际情况并不相符.说明电源的外电路短路时电动势并不等于开路时的电动势,这也说明电源的电动势可能与外电路电阻的大小有关.下面我们探究该题模式下电动势的变化规律. 由原题第(3)问解答,外电路电压为U时,单位时间内有N′个光电子由A板运动至B板,电路中的电流为I′=N′e,N′个光电子从A板向B板运动时动能的损失之和ΔEk等于外电路消耗的电功率,则 P′=I′U=N′eU=ΔEk (1) (2) (3) 可见,该光电转换器作为电源来说,如果定义该电源的电动势只是电路开路时A,B两板间的电压时,其电动势只与金属材料和入射光的频率有关,与外电路负载无关,但其电路内外电压之和随外电路电阻变化而变化,并不是一个定值. 5.4 对电源内阻的分析 内阻形成的本质原因较为复杂,本文不作讨论,仅从高中物理角度作肤浅说明:可以理解为当光子打到B板时,由于碰撞使得B板的微观粒子的无规则运动加剧,阻碍了电子的定向移动,从而形成电阻.而且两板间电压U越小,碰撞的光电子数越多,碰撞越剧烈,损失的动能也越多,导致无规则运动越剧烈,内阻应越大.这与如图3[1]所示的某硅光电池的伏安特性曲线所表示的规律一致. 图3 硅光电池伏安特性曲线[1] 可求得 显然在入射光频率和金属材料一定时,这个等效内阻是一个定值,其值等于图3中U-I图线中电源开路点与短路点连线的斜率大小. 物理高考题(尤其是压轴题),不仅是对高考命题思想的体现,也是对学生综合能力强弱的评判.该题没有考查复杂电路和带电粒子在电场中的复杂运动分析,而利用光电效应和平行板电容器构建出了如此具有考查价值的原始问题,即不进行复杂模型的堆砌,而考查学生对物理思想的建立和物理模型的理解,体现了北京物理试题有别于其他省市的风格.试题书写量看上去很少,也没有复杂的推导和运算,但确能考查学生的建模能力和对物理模型的深度理解,这种考查方式才更加符合高中阶段新课改对学生进行物理教育的目标.只有这样,才是真正把学生从题海中解放出来,享受物理思考的乐趣[3]. 另一方面,我们也应反思,在平时教学过程中,不能太过功利,传授大量所谓的模型和解题技巧,不能生搬硬套已有的模型化习题,否则学生很有可能面对实际问题时会陷入“有劲使不上”的学习困境.所以我们应当深入分析物理问题,多角度思考物理情形,从物理思想本源入手,注重物理学科思想方法的习得过程,真正生成具有应用价值的物理规律,真正形成解决问题的能力. 1 张玮,杨景发,闫其庚.硅光电池特性的实验研究.实验技术与管理,2009(9):42~46 2 卢德馨.大学物理学(第2版).北京:高等教育出版社,2003.293 3 崔琰,李莜娜.2013年北京高考物理压轴题的解析与思考.物理教师,2013(7):77~78 2015-09-27)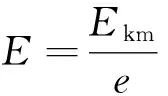
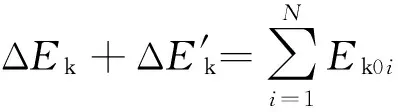
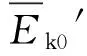
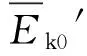
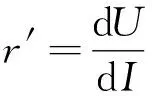
6 反思

