“慢星参考系”法速解“天体追及”问题

石 睿

(福州第一中学 福建 福州 350108)



中学物理教学

“慢星参考系”法速解“天体追及”问题

石 睿

(福州第一中学 福建 福州 350108)

提出用“慢星参考系”法解决高中物理教学中的难点与热点问题——“天体追及”问题.

慢星参考系 天体追及问题

“天体追及”问题是万有引力与航天版块中的一个难点，也是近年高考中的热点.在这类问题中，找到各天体运动的角度关系往往是解题的关键，而对大部分学生而言，这也是较难完成的部分.在实际教学中，可以尝试“以慢星为参考系”的方法，帮助学生迅速、准确找到角度关系，解决“天体追及”问题.

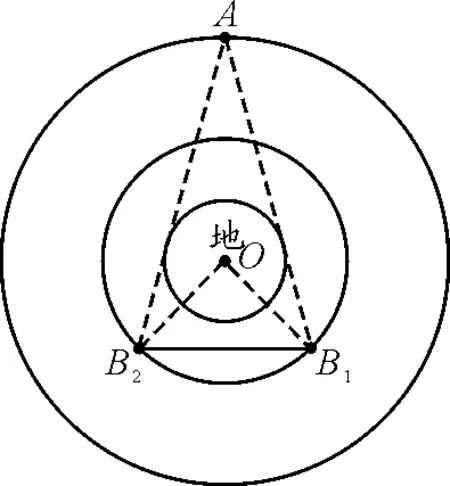
图1

【例1】(2010年高考上海物理卷第24题)如图1所示，3个质点a，b，c质量分别为m1，m2，M(M≫ m1，M≫ m2).在c的万有引力作用下，a和b在同一平面内绕c沿逆时针方向做匀速圆周运动，轨道半径之比ra∶rb=1∶4,则它们的周期之比Ta∶Tb=______;从图示位置开始，在b运动一周的过程中，a，b，c共线了______次.

解析：由开普勒第三定律易得

Ta∶Tb=1∶8

第2个空下面介绍两种解法.

解法1：

设从开始到共线时，a和b转过的角度分别为θa与θb，初始时a，b间的夹角为θ0，则第一次共线时，a，b分居c两侧，即

θa+θ0-θb=π

第二次共线时，a，b在同一侧，即

θa+θ0-θb=2π

易知，第n次共线时，应有

θa+θ0-θb=nπ

即

(1)

可得

解法2：

设a的角速度为ωa，b的角速度为ωb，ωa>ωb，则称a为快星，b为慢星.

若以慢星b为“参考系”，将b看作不动，易得共线时a相对于b转过的角度为nπ-θ0，而a相对于b的角速度ωab=ωa-ωb，则

ωabt=nπ-θ0

即

(2)

可以看出，得到的角度关系式(2)与式(1)相同.

【例2】(2014年高考全国大纲卷物理第26题)已知地球的自转周期和半径分别为T和R，地球同步卫星A的圆轨道半径为h，卫星B沿半径为r(r

(1)卫星B做圆周运动的周期；

(2)卫星A和B连续地不能直接通讯的最长时间间隔(信号传输时间可忽略)．

解析：(1)根据开普勒定律和圆周运动规律可得

(3)

(4)

(5)

由式(3)～(5)，可得

图2

图3

【例3】(2014年高考全国新课标Ⅰ卷)太阳系各行星几乎在同一平面内沿同一方向绕太阳做圆周运动.当地球恰好运行到某地外行星和太阳之间，且三者几乎排成一条直线的现象，天文学称之为“行星冲日”.据报道，2014年各行星冲日的时间分别为：1月6日木星冲日；5月11日土星冲日；8月29日海王星冲日；10月8日天王星冲日.已知地球及各地外行星绕太阳运动的轨道半径如表1所示，则下列判断正确的是

表1 各行星绕日运动的轨道半径

A．各地外行星每年都会出现冲日现象

B．在2015年内一定会出现木星冲日

C．天王星相邻两次冲日的时间间隔为土星的一半

D．地外行星中，海王星相邻两次冲日的时间间隔最短

解析：以慢星(地外行星)为“参考系”，设某颗地外行星相邻两次冲日的间隔时间为t，在t内，地球相对行星转过2π ，则有

即

(6)

由于选项中时间单位为“年”，故将T地=1年代入式(6)，得

(7)

故选项A错.

以AU和年为单位，由开普勒第三定律得

(8)

由式(7)、(8)及表1中的数据，易知选项D正确，且可得

故选项B正确.

由式(7)、(8)及表1中数据，计算可知选项C错误.

本题除了运用慢星参考系之外，还将周期T以“年”，轨道半径R以“AU”为单位，使得计算得到简化.

1 高正球，金凤权.天体运动中“追及问题”的解法探究.物理教师，2009(8)：53～54

2 刘文欣.巧选参考系在天体“追及相遇”问题中的应用.物理教师，2014(2)：84～85

2015-09-11)