基于瞬心法的麦弗逊悬架特性分析与改进设计
李 强
(合肥工业大学 机械与汽车工程学院,安徽 合肥 230009)
基于瞬心法的麦弗逊悬架特性分析与改进设计
李 强
(合肥工业大学 机械与汽车工程学院,安徽 合肥 230009)
文章提出了一种基于瞬心法进行麦弗逊悬架运动特性分析与优化设计的方法。该文以某款麦弗逊式悬架为研究对象,基于瞬心法对麦弗逊式悬架进行运动学分析,在此基础上构建了基于ADAMS的麦弗逊式悬架仿真模型,与试验数据的对比结果表明了所建模型是准确的;将灵敏度分析法与瞬心法下的运动学分析相结合,分析了下摆臂关键点变化对车轮定位参数的影响程度。该文的研究为该款车辆的悬架设计提供了参考。
瞬心法;麦弗逊悬架;灵敏度分析;改进设计
麦弗逊式独立悬架由于结构简单、非簧载质量小、成本低廉等优点,成为中低端汽车悬架的一种主要形式。麦弗逊式悬架设计成功与否主要由车辆定位参数和轮距等性能决定[1]。目前,国内外学者主要通过多刚体动力学软件分析[2-3]或矢量法[4-5]对麦弗逊悬架运动特性进行分析,取得了诸多研究成果。
本文以需加大轮距的某乘用车为研究对象,基于瞬心法推导出麦弗逊悬架的数学方程,通过灵敏度分析的方法对该前悬架下摆臂坐标进行分析,在此基础上进行下摆臂关键点设计。
1 麦弗逊悬架运动学分析
1.1 悬架模型
某A0级轿车前麦弗逊悬架模型如图1所示。
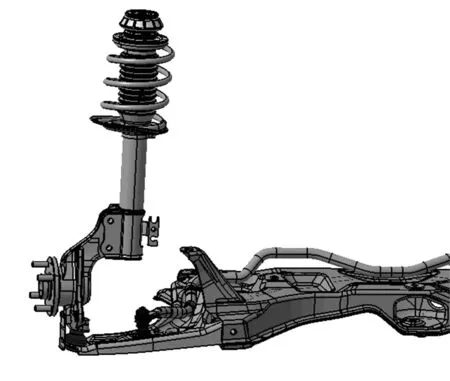
图1 左前轮悬架三维模型
在汽车坐标系下,实测三维数学模型的各硬点坐标见表1所列。
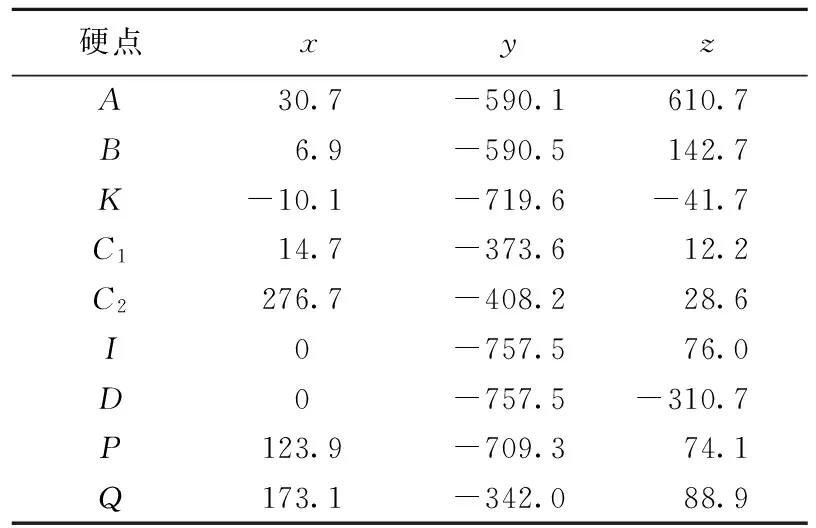
表1 左悬架各硬点坐标
1.2 基于瞬心法的运动学分析
悬架结构简图如图2所示。其中,A为悬架上端固定点球销中心;AK为虚拟主销轴线;I为车轮中心;E为外端面圆心,用以确定前轮外倾角和前束角;IE长度为车轮断开面宽度的1/2;C为下摆臂的摆动中心;C1C2为下摆臂转动轴线;D为轮胎接地点。当轮胎上下跳动时,A、Q、C1、C2位置坐标保持不变;连接转向节的4个铰点I、B、P、K的相对位置保持不变;KC、PQ不变。
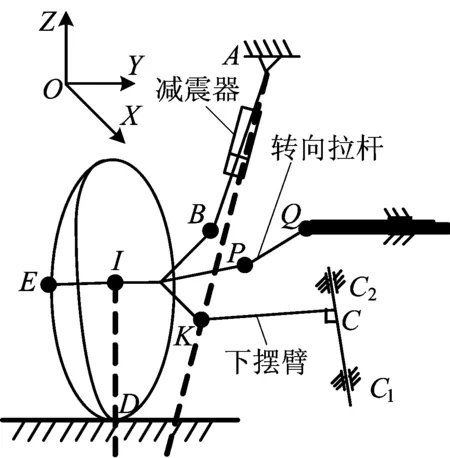
图2 悬架结构简图
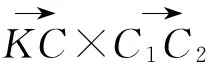
(1)
其中,G1为由整体坐标系OXYZ到局部坐标系O1X1Y1Z1的变换矩阵;K、C为K点和C点在OXYZ中的坐标矩阵;GX(α)为绕X1轴旋转的坐标变换矩阵,即
本文仅以左侧悬架和车轮为例,则车轮可视为绕悬架系统的瞬心轴线作圆周运动,同时瞬心轴线随着轮胎的上下跳动随时发生变化[6]。在某一特定时间,确定瞬心轴线的方法如下:当悬架运动到某一位置时,作1个垂直于主销过悬架上端固定点A的平面,与KC(C为K到下摆臂转动轴线C1C2的垂足)的延长线交于空间一点T,则T点为悬架在此运动位置的瞬心,作瞬心T垂直于平面ACT的直线为悬架在此运动位置的瞬心轴,如图3所示。其中,T为悬架的运动瞬心;W为侧倾中心;B为轮距。由此可以认为,左侧悬架绕瞬心轴作旋转运动,设转动角为β。
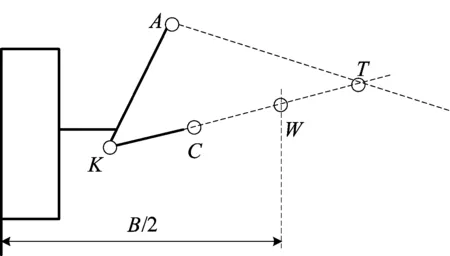
图3 车轮跳动时的运动瞬心和侧倾中心
直线TK的方程为:
(2)
过点A与直线AK垂直的平面方程为:
(3)
求解(2)式和(3)式即可求出瞬心T。
在轮胎的跳动量相对较小时,可近似认为:
(4)
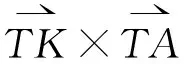
(5)
其中,G2为由整体坐标系OXYZ到局部坐标系O2X2Y2Z2的变换矩阵;GX(β)为绕X2轴旋转的坐标变换矩阵。
同理可求得在下摆臂KC摆动α角、悬架绕运动瞬心轴转动β角后,B、P、I、E、D点在整体坐标系中的坐标Bβ、Pβ、Iβ、Eβ、Dβ。确定了上述各坐标点的动态值之后,即可分析出前轮外倾角、前束角、主销后倾角、主销内倾角等评价参数的计算公式,进而根据四轮定位参数的变化来分析悬架的运动特性。
主销后倾角、主销内倾角、前轮外倾角、前束角的计算公式分别为:
(6)
(7)
(8)
(9)
1.3 麦弗逊悬架模型验证
根据(6)~(9)式,输入下摆臂外球铰点K的Z向跳动量±50 mm,计算步长为5 mm,可获得基于瞬心法的前轮外倾角、前束角和主销内倾角的变化曲线。
为了验证所建模型的准确性,基于ADAMS/Car软件构建麦弗逊悬架仿真模型,结果如图4所示。
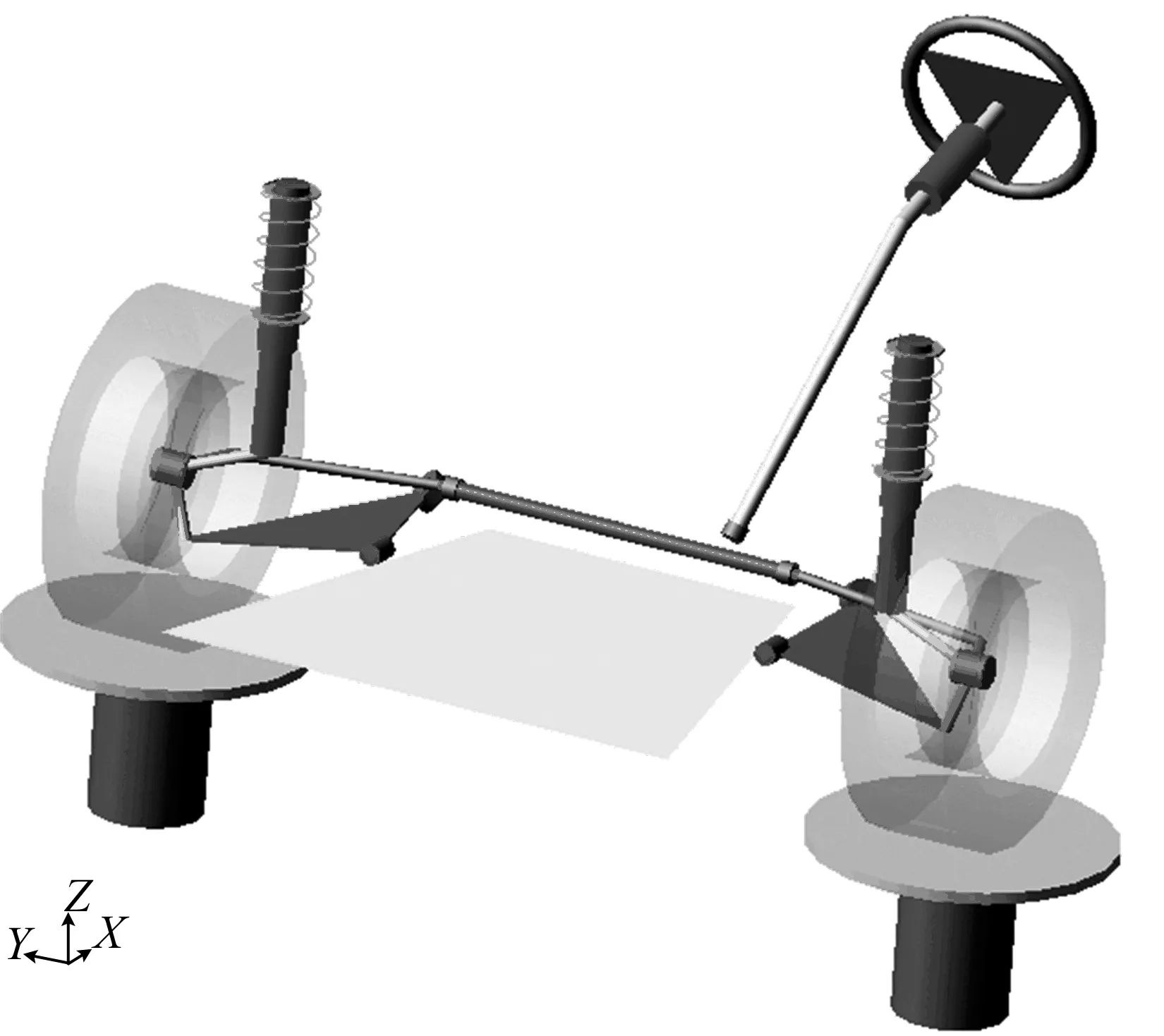
图4 ADAMS/Car运动仿真模型
定位参数仿真与计算结果的对比如图5所示。对比计算结果和仿真结果可知,两者的定位角误差较小。
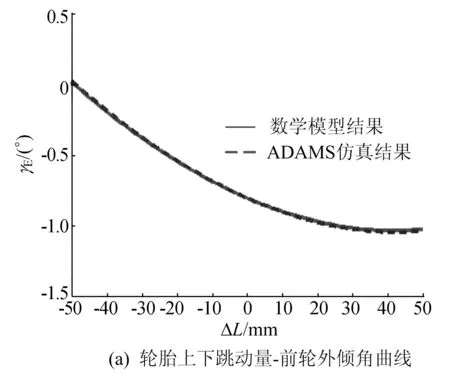
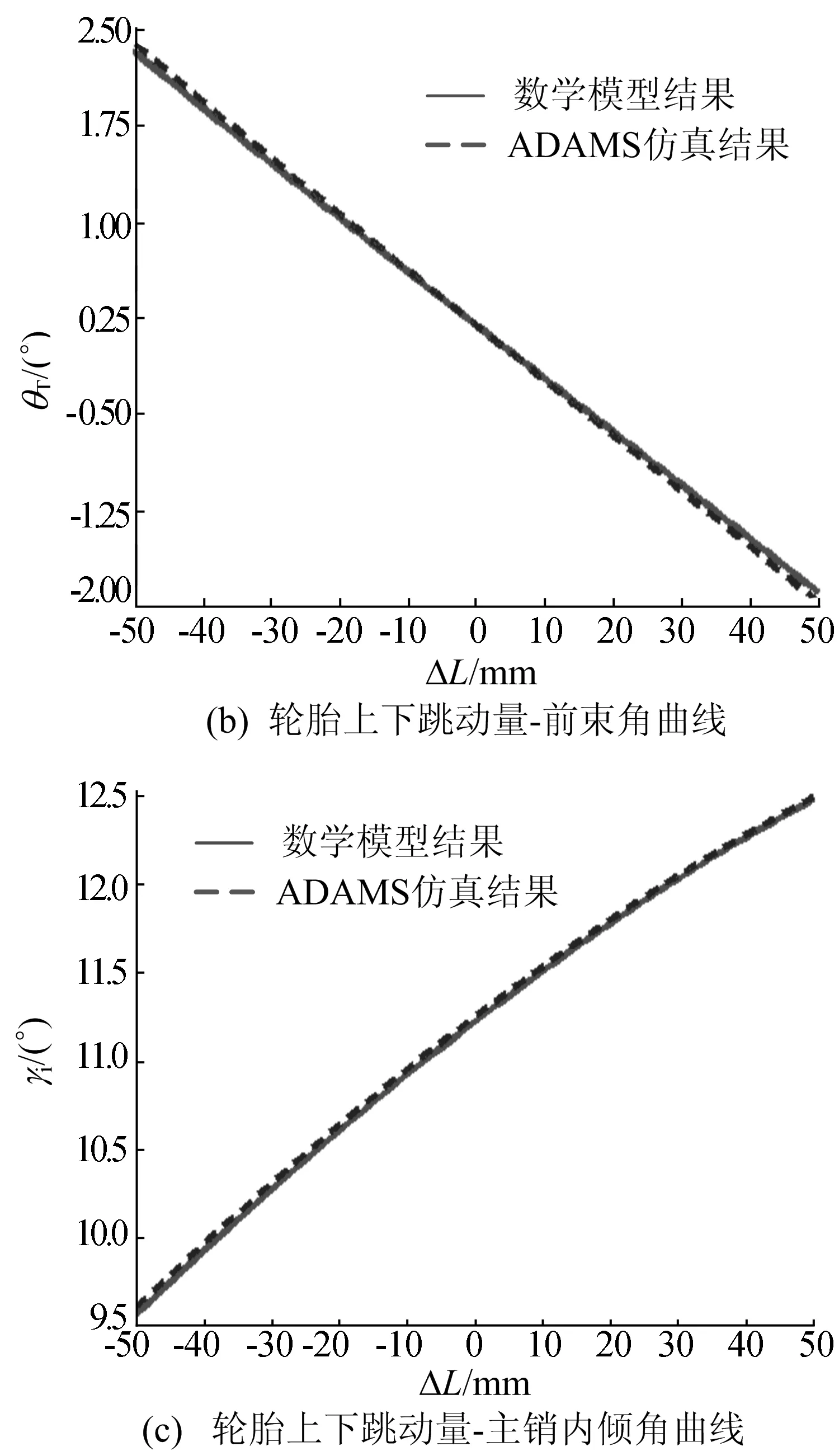
图5 定位参数仿真计算结果的对比
2 下摆臂关键点设计
2.1 基于灵敏度分析的影响分析
车轮定位参数的好坏直接影响操纵稳定性、转向轻便性以及轮胎磨损等性能,而悬架各关键点位置又直接影响各定位角。该款乘用车需要对其轮距加大20 mm,为了尽可能减少车辆的变化,采用对其前悬架下摆臂安装点进行改进的措施。
选择下摆臂外点K作为关键点分析,并使用未知变量值(x,y,z)代替K坐标,再对前轮外倾角、前束角分别求对未知变量的偏导数,获得的灵敏度函数如下:
(10)
(11)
根据(10)式和(11)式,可分别求出下摆臂外点的坐标变化对外倾角和前束角的影响程度。利用Matlab软件,结合上述灵敏度理论函数[7-8],作三维瀑布图。
外倾角和前束角随轮胎上下跳动量的x向、y向、z向变化曲面分别如图6~图8所示。其中,横坐标为轮胎上下跳动量;纵坐标为将下摆臂外点的3个坐标值进行加大或减小时的结果(根据汽车正向设计过程中轮距、车身高度等整车尺寸合理选择出变化范围)[9-11];竖坐标分别为前轮外倾角和前束角。
分析图6和图7可知:① 轮胎上下跳动时,前束角随着y值的减小而先减小后变大,因此为了使前束角在0°附近变化且不易过大,x值可适当减小10 mm,y值则增大2 mm,这样既可满足车辆凹凸行驶时的稳定,也可以减小对轮胎的磨损;② 改变该点坐标会引起主销内倾角和后倾角的变化;x值减小时会引起主销后倾角的增加,同时主销后倾拖距有所增加,会提高整车的转向回正能力,特别在轮胎上下跳动过程中的增加会提高整车稳定性;y值增加会提高主销内倾角、降低主销偏置距,适当增加内倾角具有提高转向回正能力,但是增加过多会转向沉重,加速轮胎磨损等[12-13],因此不建议增加过多。
分析图8可知,随着下摆臂外点z值的增加,轮胎上下跳动过程中外倾角会有所降低,负的外倾角会提高整车在跳动过程中的稳定性,因此可适当增加该距离。但杆增长后会伴随着弹性运动,可能引起振动问题,因此可通过坐标值z向增加对外倾角进行优化,保证汽车在下跳时具有正向外倾角和上跳时存在较弱的外倾趋势,从而达到转向所需的附着力和稳定性。
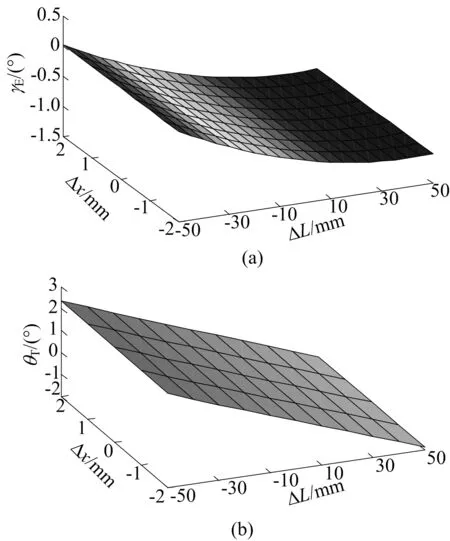
图6 x向外倾角和前束角随轮胎上下跳动量的变化曲面
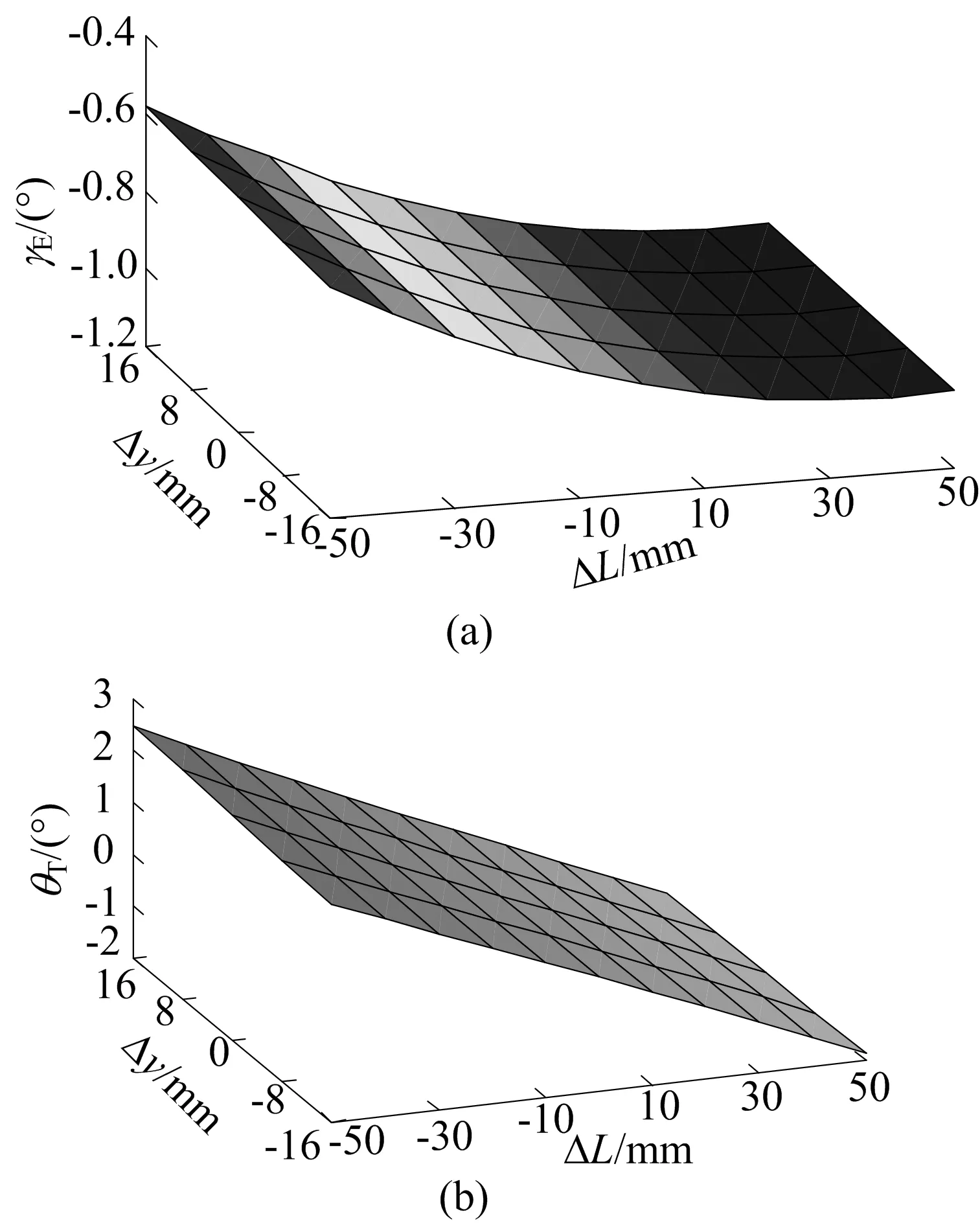
图7 y向外倾角和前束角随轮胎上下跳动量的变化曲面
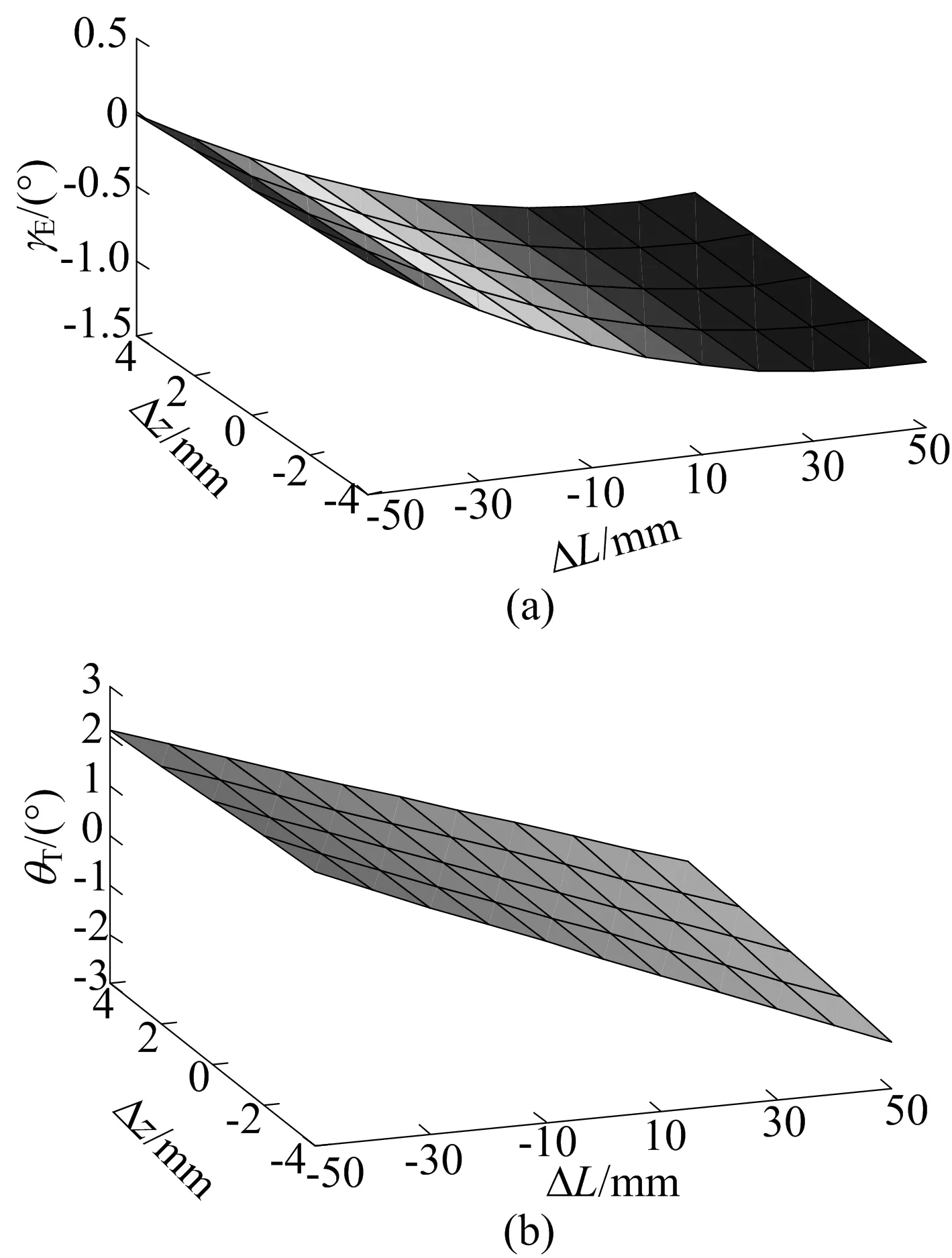
图8 z向外倾角和前束角随轮胎上下跳动量的变化曲面
2.2 下摆臂关键点结构改进及对比分析
根据以上灵敏度分析结果,改进前、后悬架的关键硬点坐标参数对比见表2所列。

表2 关键硬点坐标优化前、后对比
结构改进后的车辆在JLU-I型悬架试验测试台上进行测试,结果如图9所示。
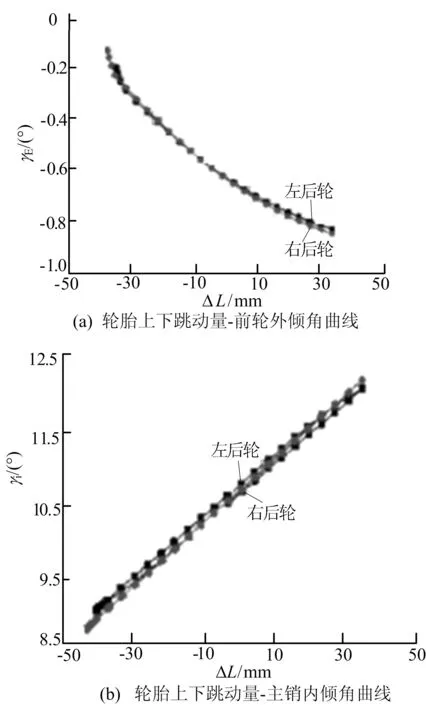
图9 运动特性试验结果
3 结 论
(1) 本文基于瞬心法进行了麦弗逊式悬架运动学分析,并与ADAMS软件建立的悬架模型进行了仿真结果对比,验证了所建模型的正确性。
(2) 基于灵敏度分析进行了下摆臂关键点变化对定位参数的影响分析,在此基础上进行了前悬架下摆臂定位点坐标设计,并通过实车试验验证了分析结果的正确性。
[1] 王望予.汽车设计[M].北京:机械工业出版社,2004:174-217.
[2] 陆建辉,周孔亢,郭立娜,等.电动汽车麦弗逊前悬架设计及参数优化[J].机械工程学报,2012,48(8):98-103.
[3] 夏长高.麦弗逊式独立悬架特性[J].农业机械学报,2004,35(6):1-4.
[4] 张洪欣,陈欣.滑柱摆臂式悬架的矢量分析方法[J].汽车技术,1989(3):17-22.
[5] 古玉锋,吕彭民,单増海,等.转向杆系空间结构非线性建模与分析[J].农业机械学报,2014,45(10):7-14.
[6] 陈黎卿,郑泉,王启瑞.麦弗逊式独立悬架导向机构的运动特性[J].拖拉机与农用运输车,2005(5):57-60.
[7] 王蠡,项党,陈璟,等.扭力梁后桥总成参数对整车转向特性影响分析[J].汽车工程,2011,33(1):60-64.
[8] 张鹏,王浩,陈黎卿.基于灵敏度分析的某扭力梁悬架的优化[J].中国机械工程,2016,27(1):46-51.
[9] 项昌乐,廉晓辉,周连景.针对实际传动系统灵敏度分析与动力学修改[J].中国机械工程,2006,17(3):325-328.
[10] 张代胜,王浩.基于灵敏度分析的汽车动力传动系扭振特性优化[J].中国机械工程,2013,24(5):685-689.
[11] 张代胜,张林涛,谭继锦,等.基于刚度灵敏度分析的客车车身轻量化研究[J].汽车工程,2008,30(8):718-720.
[12] 靳立强,宋传学,彭彦宏.基于回正性与轻便性的前轮定位参数优化设计[J].农业机械学报,2006,37(11):20-23.
[13] 马骏,钱立军.前轮定位参数优化设计和试验的研究[J].汽车工程,2014,36(2):231-235,242.
(责任编辑 胡亚敏)
Characteristic analysis and optimization design of McPherson suspension based on instantaneous center method
LI Qiang
(School of Machinery and Automobile Engineering, Hefei University of Technology, Hefei 230009, China)
A method of motion characteristic analysis and optimization design of McPherson suspension based on the instantaneous center method is presented. The kinematic analysis of a McPherson suspension is carried out by using the instantaneous center method, and the corresponding simulation model is built in ADAMS. The mathematical model is validated through the comparison of the experimental results with the simulation results of ADAMS model. With the integration of sensitivity analysis and the presented kinematic analysis, the effect of the structural parameters of the lower control arm on the wheel alignment parameters is studied. The study provides a reference for the optimization design of the suspension system of this vehicle.
instantaneous center method; McPherson suspension; sensitivity analysis; optimization design
2016-06-29;
2016-08-17
安徽省高校自然科学重点资助项目(kj2015a305)
李 强(1977-),男,山东胶南人,合肥工业大学工程师.
10.3969/j.issn.1003-5060.2016.11.007
U463.2
A
1003-5060(2016)11-1472-05

