n元二次型的一个几何度量定理

姚云飞, 唐 剑, 王先超, 姚 磊

(1.阜阳师范学院 数学与统计学院,安徽 阜阳 236037; 2.中央财经大学 金融学院,北京 100081; 3.阜阳师范学院 经济学院,安徽 阜阳 236037)



n元二次型的一个几何度量定理

姚云飞1, 唐 剑1, 王先超1, 姚 磊2,3

(1.阜阳师范学院 数学与统计学院,安徽 阜阳 236037; 2.中央财经大学 金融学院,北京 100081; 3.阜阳师范学院 经济学院,安徽 阜阳 236037)

文章从代数学出发,以分析学为工具,获得了n元二次型的一个几何度量定理,并由此将一批几何度量的问题系统化,且处理方法简捷,推广了前人的相关结果。该文的方法与结果对从事金融数学、统计学等研究有一定的参考价值。

二次型;正交变换;几何度量

0 引 言

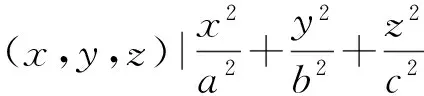
设X=(x1x2…xn1)T,XT表示X的转置,矩阵A的行列式记为|A|,矩阵A的元素aij的代数余子式记为Aij。

1 引 理

引理1 假设如下：

(1) 矩阵

是实对称矩阵。

(2) 二次型

若

则有：

(Ⅰ) 二次型f(x1,x2,…,xn)经过平移后

其中

(Ⅱ) 二次型f(x1,x2,…,xn)通过两步正交变换(平移与旋转)可以化为

其中,λi(i=1,2,…,n)为矩阵B的特征值

证明 (1) 由An+1,n+1≠0及Cramer法则知,方程组

有唯一解

由AT=A和文献[1]中的定理3知：

而平移后的二次型f(x1,x2,…,xn)的二次项系数不发生变化。事实上,令

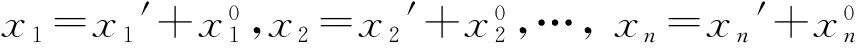
即

亦即

故

于是,有

则由(Ⅰ)知：

由文献[3]中的定理8知,存在正交变换,使得:

于是,有

其中,λi(i=1,2,…,n)为矩阵B的特征值。故引理1(Ⅱ)成立。

在引理1(Ⅱ)中,当n=3时,便得到文献[1]中结果;但文献[1]中的d*表达式较繁,不易操作。而由本文引理2可知,d*=|A|/A33,这对于曲面分类的研究,使用更加方便。

引理2 设正交变换σ如下:

若f(x1,x2,…,xn)在有界闭区域Ω上连续,则有：

特别地,在正交变换下,当Ω为球时,Ω=Ω′。

2 定 理

定理1(二次型的一个几何度量) 设矩阵A为实对称矩阵,若

(1) 矩阵B是正定矩阵。

(2) |A|<0。

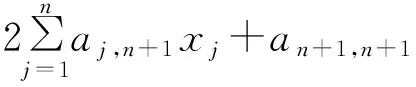
在欧氏空间Rn中的“体积”为：

证明 因为|B|=An+1,n+1且B是正定矩阵,所以An+1,n+1>0。由引理1(Ⅱ)知：

经过两步正交变换(平移与旋转)可以化为：

其中,λi(i=1,2,…,n)为矩阵B的特征值。由矩阵B的正定性知λi>0,i=1,2,…,n。于是,由f(x1,x2,…,xn)≤0知：

从而,有

由|A|<0知：

(1)

已知

记

由引理2知：

若设

则由(1)式得：

(2)

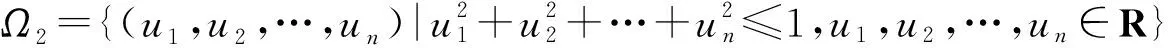
其中，Γ(x)为Gamma函数。

文献[2-5] 中的一些结果均为定理1的特例,且处理方法简捷、统一。具体的以特例形式表述如下。

特例1 在定理的条件下,若

(1)a1,n+1=a2,n+1=…=an,n+1=0,

an+1,1=an+1,2=…=an+1,n=0。

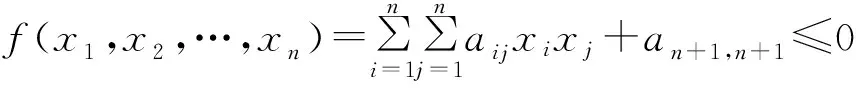
由特例1知:

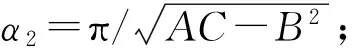
上述结果比文献[3]中问题6的处理方法更简单。

Ax2+By2+Cz2+2Fyz+2Gzx+2Hxy=1

上述结果比文献[3]中问题10的处理方法更简单。

(3) 若a>0,则二次曲面

x2+y2+z2+xy+yz+zx=a2

特例2 在特例1的条件下,当i≠j时,ai,j=0,其中i,j∈{1,2,…,n}。若将

在欧氏空间Rn中的“体积”记为βn,则

由特例2知：

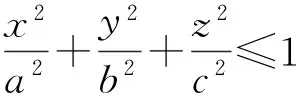
(3) 若

则

即文献[5]中问题3的结果。

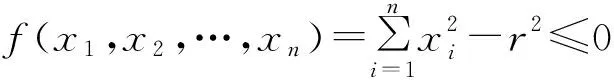
上述结果为文献[5] 关于λ(B(x,a))的结果。

由特例3知

(1) 在R1中,线段x2≤r2的长度ω1=2r。

(2) 在R2中,圆盘x2+y2≤r2的面积ω2=πr2。

(3) 在R3中,球x2+y2+z2≤r2的体积ω3=4/3πr3。

特例4 设aij=aji,i,j=1,2,3。若矩阵

在欧氏平面R2中的面积为：

上述结果即为文献[3]中问题7的结果,且比文献[3]的处理方法更简单。特例1的(1)、特例2的(1)、特例3的(2)均是特例4的特例。特例4在平面解析几何、第二型曲线积分等方面都有广泛的应用。

特例5 设aij=aji,i,j=1,2,3,4。若矩阵

是正定矩阵,

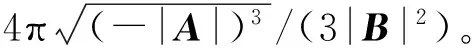
特例1的(2)、(3),特例2的(2)以及特例3的(3)均是特例5的特例。

3 结 论

本文证明了n元二次型的一个几何度量定理,由特例1～特例5知,一批已有的几何度量(长度、面积、体积等)都是该定理的特例,由此可将上述几何度量问题进行统一处理,且处理方法更加简便。

[1] 北京大学数学系前代数小组.高等代数[M].4版.北京:高等教育出版社,2015:79-394.

[2] 胡适耕,姚云飞.数学分析:定理·问题·方法[M].北京:科学出版社,2007:166-167.

[3] 菲赫金哥尔茨.微积分学教程(第2卷)[M].8版.徐献瑜,冷生明,梁文骐,译.北京:高等教育出版社,2014:162-174.

[4] 吉米多维奇.数学分析习题集[M].李荣冻,译.北京:人民教育出版社,1978:219-389.

[5]JONESF.LebesgueintegrationonEuclideanspace[M].RevisedEdSudbury:JonesandBartlettPublishers,2010:206-207.

[6]POLGAG,SEGOG.Problemsandtheoremsinanalysis[M].Berlin:Springer-Verlag,1972:143-145.

[7] 姚云飞.正交变换在重积分中某些应用[J].数学的实践与认识,2003,33(9):139-144.

[8] 姚云飞.论二次型与正交变换在重积分中的某些应用[J].工科数学,2002,18(6):90-102.

(责任编辑 朱晓临)

A theorem of geometric measure aboutn-ary quadratic form

YAO Yunfei1, TANG Jian1， WANG Xianchao1， YAO Lei2,3

(1.School of Mathematics and Statistics, Fuyang Normal University, Fuyang 236037, China; 2.School of Finance, Central University of Finance and Economics, Beijing 100081, China; 3.School of Economics, Fuyang Normal University, Fuyang 236037, China)

A theorem of geometric measure aboutn-ary quadratic form is given from the perspective of algebra by means of analytics, which can make a large number of geometric measure problems become systematic in a simple process. It extends some related results. These methods and results have positive reference value among the research of financial mathematics, statistics and other fields.

quadratic form; orthogonal transformation; geometric measure

2016-08-07

国家自然科学基金资助项目(11401104);全国统计科学(重点)资助项目(2015LZ42;2011LY094);国家特色专业资助项目(TS11496)和阜阳师范学院重点学科资助项目(2010XK-03)

姚云飞(1956-),男,安徽合肥人,阜阳师范学院教授.

10.3969/j.issn.1003-5060.2016.11.028

O151.1; O172.2

A

1003-5060(2016)11-1580-05