基于非对称悬索桥的振动基频估算公式
杨国俊, 郝宪武, 宋 涛, 李子青
(1.兰州理工大学 土木工程学院,甘肃 兰州 730050; 2.长安大学 公路学院,陕西 西安 710064)
基于非对称悬索桥的振动基频估算公式
杨国俊1, 郝宪武2, 宋 涛2, 李子青2
(1.兰州理工大学 土木工程学院,甘肃 兰州 730050; 2.长安大学 公路学院,陕西 西安 710064)
为了便于快速计算非对称悬索桥的振动基频,文章基于主缆不等高支撑的悬索桥,应用Rayleigh法,分别推导了一阶竖弯和扭转振动基频估算公式,对于一阶正对称的竖弯和扭转基频,提出了修正规范公式的非对称结构参数影响因子,并推导了扭弯基频比公式,最后通过有限元法验证估算公式的精度。研究结果表明:非对称悬索桥一阶反对称的竖弯和扭转基频不受非对称结构参数的影响,而对于一阶正对称竖弯和扭转基频,当非对称结构敏感性参数ξ大于0.1时,基频减小的幅度明显显著;推导的估算公式计算解与有限元解的误差能满足设计阶段的要求,该公式可以方便指导非对称悬索桥的方案选择和初步设计。
桥梁工程;非对称悬索桥;基频; Rayleigh法;估算公式
悬索桥动力分析中的自振特性是许多研究者普遍关注的结构特性之一,结构基频影响到结构抗风的稳定性和对地震荷载的动力响应,所以计算其自振频率和振型是悬索桥设计阶段不可或缺的一环[1-2],但是在某些地区尤其山区,桥址受地形的限制,为了更好地适应这种特定的工程环境而出现了非对称的悬索桥[3],同样在设计阶段需要对其动力特性进行初步估算。文献[4]基于单跨悬索桥给出了估算一阶正对称和反对称竖弯和扭转振动基频的计算公式;文献[5]采用摄动法随机有限元(stochastic finite element method,SFEM)对桥梁结构的特征值问题进行分析,但是未给出估算基频的实用公式;文献[6-7]应用能量法推导了单跨悬索桥振动的基频估算公式;文献[8]在文献[6-7]基础上考虑了吊杆、索夹等的动能后应用Rayleigh法推导了单跨悬索桥竖向振动基频的实用近似计算公式;文献[2]采用非线性的有限元法、SAP5程序计算方法和估算法3种方法计算了吊桥的自振频率;文献[9]针对上述能量法推导的悬索桥基频近似计算公式由于没有考虑主塔刚度对自振基频的影响存在一定的误差,提出了计入边缆和主塔刚度影响和考虑实际振型修正的正对称竖弯基频估算公式;文献[10]基于3塔悬索桥采用Lanczos特征值求解法分析了中塔梁间的弹性拉索刚度对竖向振动频率的影响;文献[11-15]提出了考虑中塔刚度影响的3塔或多塔悬索桥的振动基频估算公式。
综上所述,传统对称的双塔或多塔悬索桥有相应的振动基频近似计算公式,但是针对非对称悬索桥基频的实用估算公式很少。虽然有限元法得到了广泛的应用,但是对此类桥梁来说,有限元建模过程相对复杂,不利于设计人员快速判断桥梁结构的振动特性。本文以主缆非对称的悬索桥振动基频为研究对象,应用能量法,选取合理的振型函数,推导了一阶正对称和反对称竖弯和扭转振动基频估算公式,以供概念设计或校核有限元计算结果。
1 Rayleigh法及基本假定
1.1 基于Rayleigh法的频率计算方法
假定振动不受动内力的影响,非对称悬索桥竖弯振动振型如图1所示。图1中L为主跨跨径,Hs为恒载作用下主缆的水平拉力,则竖向固有振动的微分方程[2]为:
(1)
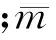
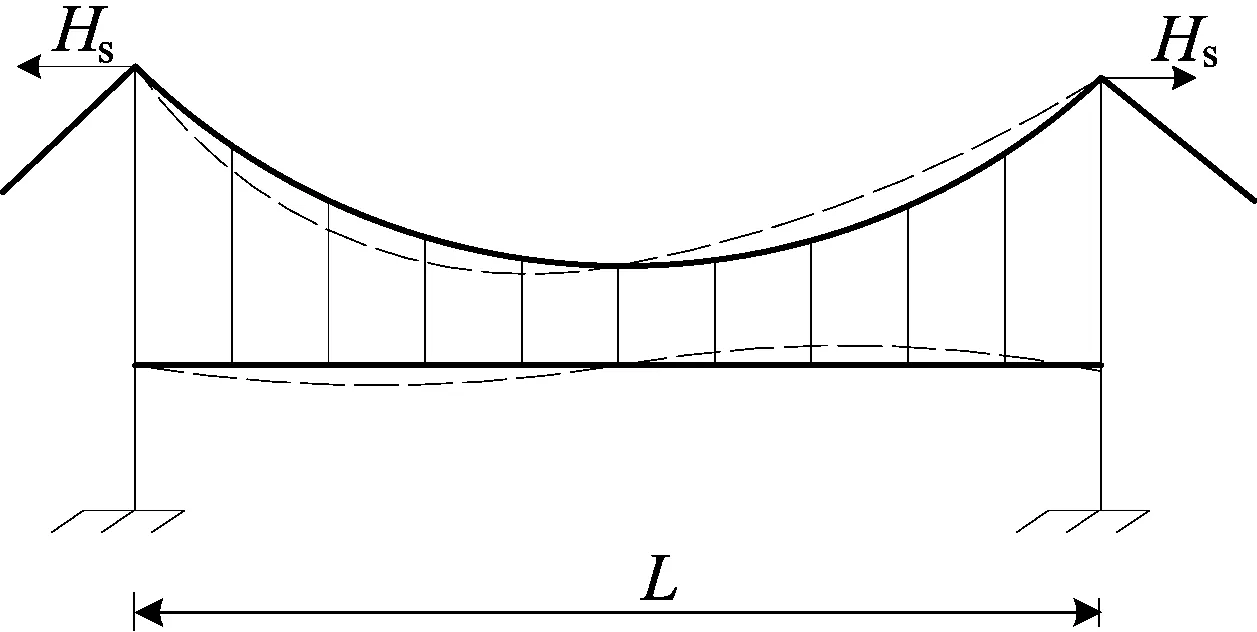
图1 非对称悬索桥竖弯振动振型
在无阻尼固有振动的情况下,桥梁的任一点、任一瞬间的位移可以表示为:
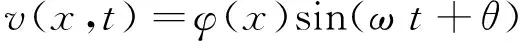
(2)
其中,φ(x)为假定的能满足桥梁位移边界条件的近似振型函数;ω为与此对应的频率;θ为相位差。
根据能量守恒原理[16]可得频率ω的近似公式为:
(3)
其中,EI(x)、m(x)分别为弯曲刚度和质量分布函数;U为体系势能;T为体系动能。
则基频f0的计算公式为:
(4)
1.2 非对称悬索桥基本假定
本文公式的推导是基于悬索桥的挠度理论,基本假定如下:① 不考虑材料非线性,所使用的材料均满足胡克定律;② 恒载在主缆上沿跨度均匀布置,主缆在恒载作用下的线形为抛物线;③ 吊索沿跨径均匀稠密布置,且在振动时不伸长不倾斜;④ 桥梁自由振动产生较小幅度的位移,且整个过程结构刚度不变;⑤ 主索鞍在主塔上不产生滑动等现象。
若两主塔的高差为h,跨中垂度为f,主跨跨径为L时,矢跨比n=f/L,定义与非对称悬索桥结构参数有关的系数ξ(主缆支承点高差与主跨跨径的比值,即ξ=h/L)为敏感性参数,非对称悬索桥如图2所示。图2中,q为主缆产生的均布荷载;α为主缆支承点连线与水平线的夹角;L1为边跨跨径。
根据基本假定,主缆线形的函数为:
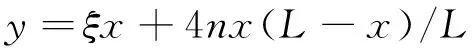
(5)
垂直方向的平衡条件为:
(6)
将(5)式代入(6)式得恒载作用下主缆水平拉力为:
(7)
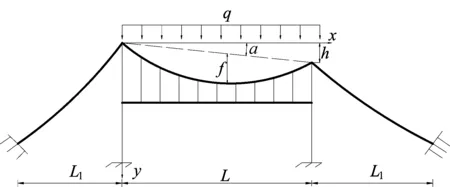
图2 非对称悬索桥在恒载作用下受力情况
2 非对称悬索桥竖弯基频估算公式
2.1 结构体系势能
非对称悬索桥铅垂平面内发生一阶弯曲振动时,其势能为主缆和加劲梁势能之和[6-9]。
(1) 主缆势能。主缆缆力变化产生的势能Uce为:
(8)
其中,Ec为主缆的弹性模量;σ为主缆的轴向应力;V为主缆体积;Ac为主缆的截面面积;Le为主缆的虚拟长度;H为振动引起的主缆水平分力。令P=1+8n2+25.6n4+1.5ξ2+16ξ2n2+0.5ξ4,有
(9)
其中,s为主缆曲线的长度。
不考虑弹性伸长,由恒载作用点降低产生的主缆重力势能(Ucg)[8]为:
(10)
因此主缆的势能Uc为:
(11)
(2) 加劲梁势能。加劲梁的弯曲势能Us为:
(12)
结构体系总势能U为:
U=Uc+Us
(13)
2.2 结构体系动能
非对称悬索桥铅垂平面内发生一阶弯曲振动时,其动能为主缆、加劲梁和吊索动能之和[6-9]。
主缆的动能Tc为:
(14)
其中,mc为两主缆质量集度之和。
加劲梁挠曲动能Tg为:
(15)
其中,mg为顺桥向加劲梁质量集度。
吊索的动能Th为:
(16)
其中,mi为第i吊索的质量集度。
所以体系总动能T为:
T=Tc+Tg+Th
(17)
2.3 一阶正对称竖向弯曲基频估算公式
对于非对称悬索桥一阶正对称竖弯自由振动,其振型如图3所示。图3中As为振动振幅。
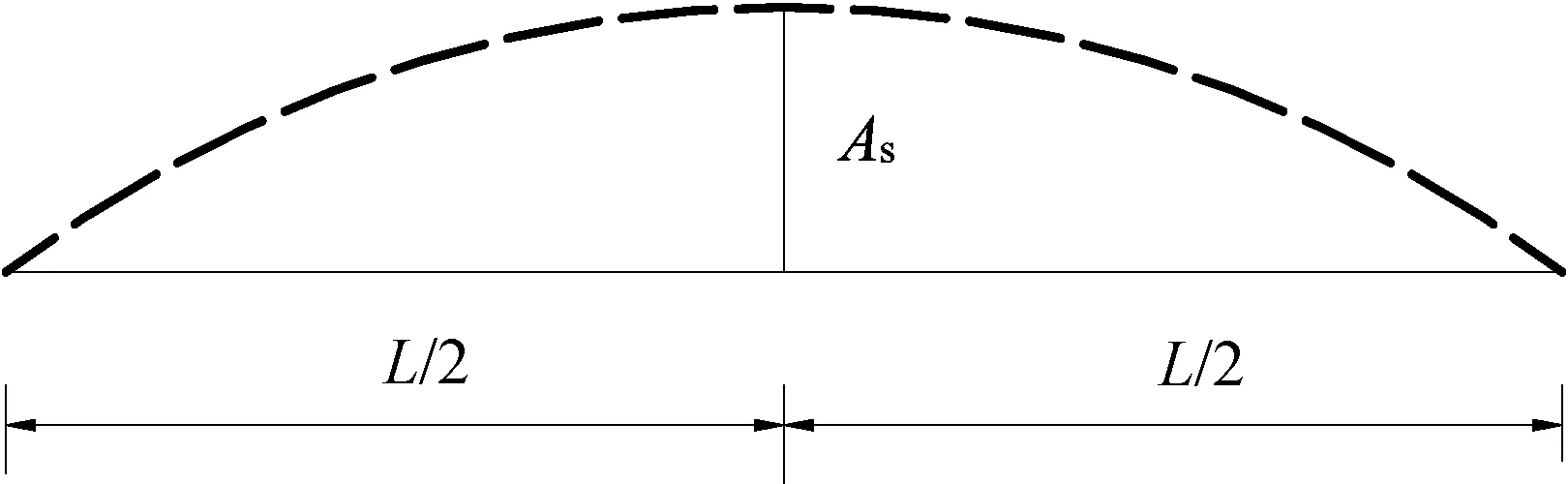
图3 一阶正对称竖弯振型
设其满足边界条件的正对称竖弯振型函数为:
(18)
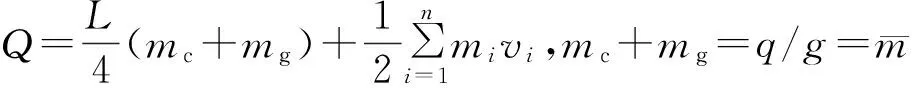
(19)
当sin(ωt+θ)=1时,体系最大总势能Umax为:
(20)
将(19)式、(20)式代入(3)式可得:
(21)
将(8)式、(20)式代入(4)式可得正对称竖弯基频fv为:
(22)
(22)式的根式运算中,分子前2项比最后一项小1~2个数量级,近似计算时可忽略不计,而吊杆质量远远小于主缆和加劲梁的质量,可忽略吊杆的动能,故(22)式可简化为:
(23)
对于非对称悬索桥,一般情况下矢跨比n=0.1,主缆虚拟长度可近似为:
正对称竖弯基频fv为:
(24)
其中,Ac1为单侧主缆的截面面积。
文献[4]中正对称竖弯基频fb估算公式为:
(25)
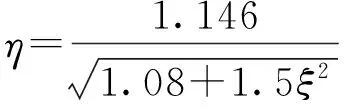
2.4 一阶反对称竖向弯曲基频估算公式
对于非对称悬索桥一阶反对称竖弯自由振动,其振型如图4所示。
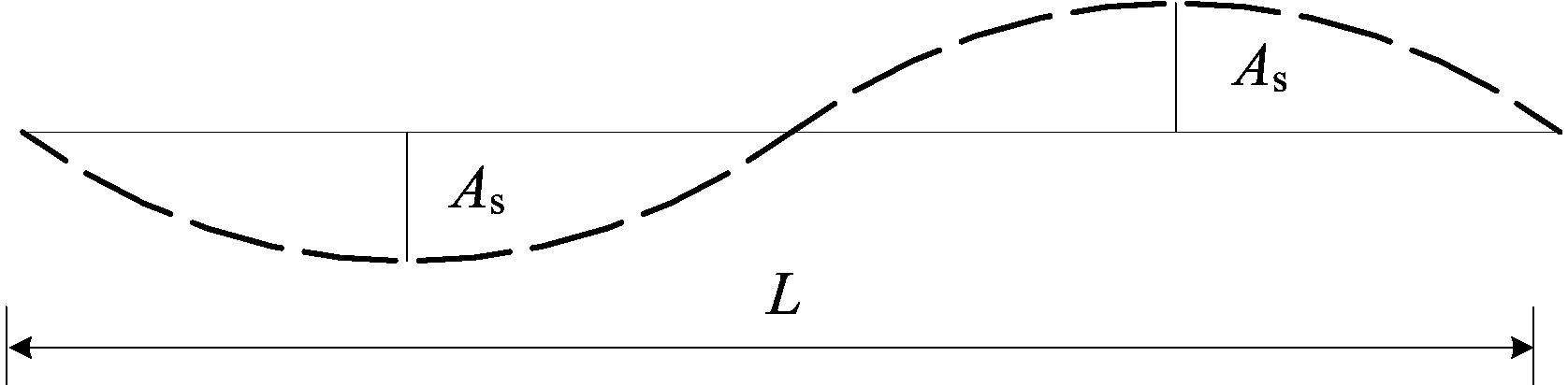
图4 一阶反对称竖弯振型
设满足边界条件的反对称竖弯振型函数为:
(26)
体系最大总动能Tmax为:
(27)
体系最大总势能Umax为:
(28)
同理可得一阶反对称竖弯基频f1的估算公式为:
(29)
同理(29)式可简化为:
(30)
文献[4]中反对称竖弯基频fb的估算公式为:
(31)
其中,Hg为恒载作用下单侧主缆的水平拉力。
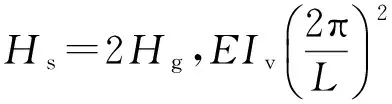
(32)
所以(31)式与文献[4,7]给出的估算公式是相同的,表明推导的非对称悬索桥的一阶反对称竖弯基频近似计算公式与单跨悬索桥的一阶反对称竖弯基频近似计算公式相同,说明与非对称结构有关的参数对一阶正对称竖弯基频没有影响。
3 非对称悬索桥扭转基频估算公式
3.1 结构体系势能
结构体系扭转振动的势能[6-7]推导如下。
加劲梁约束扭转势能U1为:
(33)
其中,EJw为加劲梁约束扭转刚度。
加劲梁自由扭转势能U2为:
(34)
其中,GIt为加劲梁自由扭转刚度。
主缆挠垂势能U3为:
(35)
其中,b为两主缆的间距。
结构体系总势能U为:
U=U1+U2+U3
(36)
3.2 结构体系动能
结构体系扭转振动的动能[6-7]推导如下。
加劲梁旋转动能T1为:
(37)
主缆挠垂动能T2为:
(38)
结构体系总动能T为:
T=T1+T2
(39)
3.3 一阶正对称扭转基频估算公式
对于一阶正对称扭转振动,设其满足边界条件的扭转振型函数为:
(40)
(41)
(42)
其中,r为加劲梁质量回转半径。
令J=mgr2+mcb2/4,将(41)式和(42)式代入(3)式得:
(43)
同理可得一阶正对称扭转基频fn估算公式为:
(44)
其中,n=0.1,Le≈L(1+8n2+1.5ξ2)。
由于(44)式的中括号内第1项远小于后2项,也就是说对于一阶正对称扭转振动,可忽略加劲梁的约束扭转的影响,(44)式可简化为:
(45)
文献[4]中一阶正对称扭转基频ft估算公式为:
(46)
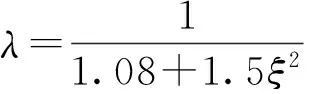
(47)
因此λ可以定义为非对称结构参数对正对称扭转基频的影响因子。
为了计算方便,将一阶正对称的扭转基频和竖弯基频比值记作扭弯基频比,对于非对称悬索桥,正对称扭弯基频比ε为:
经简化得:
(48)
3.4 一阶反对称扭转基频估算公式
对于反对称扭转振动,设其满足边界条件的扭转振型函数为:
(49)
(50)
(51)
(52)
根据前面的分析结果,同样可以忽略约束扭转的影响,故(52)式简化为:
(53)
所以(53)式与文献[4,7]给出的估算公式是相同的,即推导的非对称悬索桥的一阶反对称扭转基频估算公式与单跨悬索桥的一阶反对称扭转估算公式一致,说明与非对称悬索桥结构有关的参数不影响一阶反对称扭转的基频。
4 算例验证
某特大桥为主跨628 m的单跨主缆不等高支撑的非对称悬索桥,跨径分布为166 m+628 m+166 m,上部结构采用较好抗风性能的扁平流线型钢箱梁。设计主缆矢跨比为1/10,主缆横桥向中心间距为26 m,吊索顺向标准间距为12 m。索塔采用钢筋混凝土塔柱结构,外形为门式框架。塔体包括塔顶、上塔柱、中塔柱和下塔柱,塔柱之间设3道横梁。塔柱采用矩形空心薄壁截面。由于受地形的限制两主塔是非对称布置的,索塔高差为10.362 m,主缆支撑点高差与主跨跨径的比值为0.017,索塔左、右塔柱采用不等高形式,高塔肢高153.5 m,矮塔肢高138.5 m,加劲梁泊松比为0.3,其他参数见表1所列。
将表1中的参数代入(24) 式、(25)式、(45) 式、(46)式及(53)式,得到该桥一阶正对称和反对称竖弯和扭转基频,计算结果见表2所列。

表1 实桥结构计算参数
注:m0为对应项目单位长度质量。
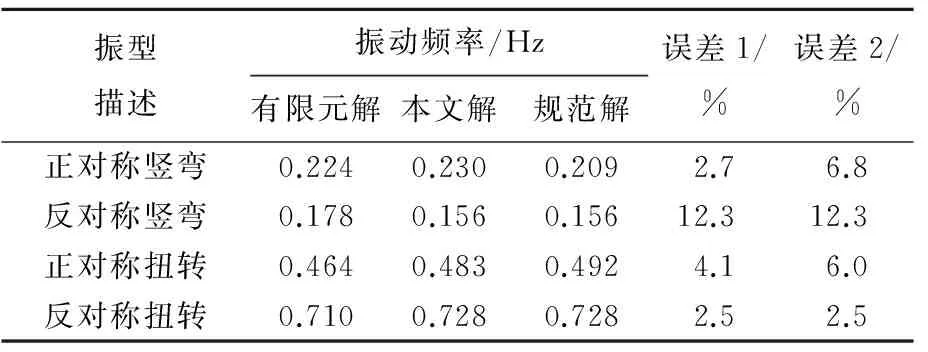
表2 不同解下实桥的一阶竖弯和扭转振动基频对比
注:误差1是本文解与有限元解之间的误差;误差2是文献[4]规范解与有限元解之间的误差。
非对称结构敏感性参数对竖向振动基频、扭转振动基频的影响分别如图5、图6所示。
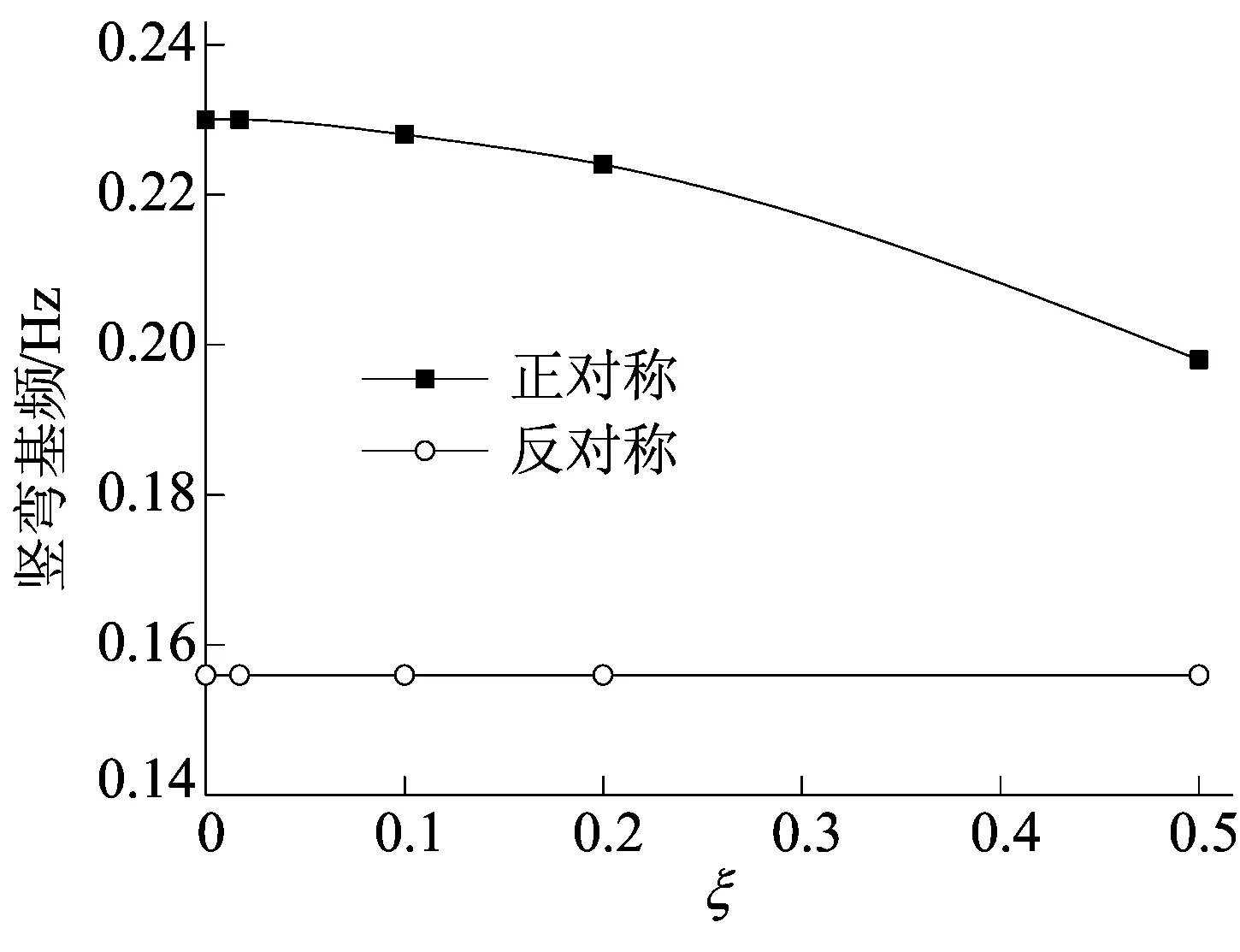
图5 结构敏感性参数对竖向振动基频的影响
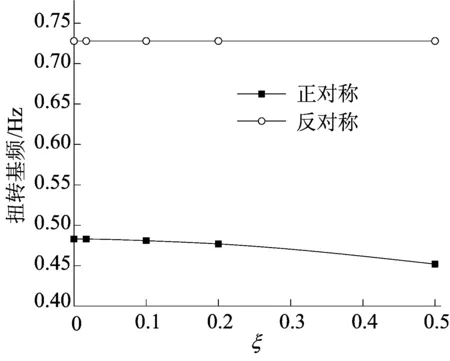
图6 结构敏感性参数对扭转基频的影响
由表2分析可知,对于非对称悬索桥的一阶正对称竖弯基频和扭转基频,推导的公式比不计入结构非对称性影响的规范公式[4]计算精度高,竖弯和扭转基频计算结果与有限元结果误差分别从6.8%、6.0%降到2.7%、4.1%,而对于非对称悬索桥的一阶反对称竖弯基频扭转基频,推导的公式与文献[4]给出的一致,说明非对称悬索桥的一阶反对称竖弯基频和扭转基频不受其相关结构参数的影响。
由图5和图6分析可知,非对称悬索桥的一阶反对称竖弯基频和扭转基频不随结构敏感性参数ξ的变化而变化,而正对称竖弯基频和扭转基频受结构敏感性参数ξ的影响,当ξ较小时,正对称竖弯基频和扭转基频变化不大,说明结构整体刚度在减小,但减小幅度不是太明显;当ξ>0.1时,基频减小的幅度较显著,表明随着主缆非对称性逐渐增大,结构的整体刚度减小幅度较显著,这些规律可以指导非对称悬索桥的初步设计。
5 结 论
(1) 推导了非对称悬索桥一阶正对称和反对称竖向振动、扭转振动的基频近似计算公式以及正对称下的扭弯基频比,提出了与非对称悬索桥有关的结构参数对正对称竖弯基频影响因子η和对正对称扭转基频影响因子λ。
(2) 分别计算了非对称悬索桥的一阶竖向弯曲自振基频和扭转振动基频,结果表明该类型桥的反对称竖弯基频和扭转基频不受非对称结构参数的影响,而对于正对称竖弯基频和扭转基频,推导的公式比不计非对称结构参数影响的文献[4]公式精度高,对于正对称竖弯基频,其计算结果与有限元计算结果的误差从6.8%降到2.7%,对于正对称扭转基频,相应的误差从6.0%降到4.1%。
(3) 对于非对称悬索桥正对称竖弯基频和扭转基频,文献[4]中的近似计算公式存在一定的缺陷,本文基于非对称悬索桥推导的实用近似计算公式只适用于主缆非对称的情况,对于跨径非对称、3塔或多塔体系及其他体系应做专门研究。
[1] REN W X,BLANDFORD G E,HARIK I E.Roebling suspension bridge:finite-element model and free vibration response [J].Journal of Bridge Engineering,2004,9(2):110-118.
[2] 肖汝诚.吊桥结构自振频率的计算方法[J].华东公路,1991(1):54-58.
[3] 李智宇.非对称悬索桥设计方法研究[D].西安:长安大学,2006.
[4] 中交公路规划设计院.公路桥梁抗风设计规范:JTG/T D60-01—2004[S].北京:人民交通出版社,2004:16-17.
[5] 刘春华,秦权.桥梁结构固有频率的统计特征[J].中国公路学报,1997,10(4):49-54.
[6] 李国豪.桥梁结构稳定与振动[M].北京:中国铁道出版社,2002:272-275.
[7] 盛善定,袁万城,范立础.悬索桥振动基频的实用估算公式[J].黄淮学刊,1994,10(1):24-31.
[8] 谢官模,王超.大跨度悬索桥竖向振动基频的实用近似计算公式[J].固体力学学报,2008,29(专辑):200-203.
[9] 鞠小华,廖海黎,沈锐利.对悬索桥对称竖弯基频近似公式的修正[J].土木工程学报,2002,35(1):44-49.
[10] 焦常科,李爱群,王浩.3塔悬索桥动力特征参数分析[J].公路交通科技,2010,27(4):51-55.
[11] 张超,黄群君,许莉.考虑主塔刚度影响的三塔自锚式悬索桥竖弯频率计算公式[J].长安大学学报(自然科学版),2014,34(6):100-106.
[12] 鞠小华.三跨连续加劲梁悬索桥基频近似公式[J].铁道工程学报,2003(2):59-63.
[13] 王本劲,马如进,陈艾荣.多塔连跨悬索桥基频估算实用公式[J].公路交通科技,2012,29(11):58-62.
[14] 张超.多塔自锚式悬索桥竖弯基频简化计算[J].武汉理工大学学报(交通科学与工程版),2013,37(4):753-757.
[15] 王本劲,马如进,陈艾荣.多塔连跨悬索桥基频估算方法[J].结构工程师,2011,27(6):54-58.
[16] 周勇军,张晓栋,宋一凡,等.高墩连续刚构桥纵向振动基频的能量法计算公式[J].长安大学学报(自然科学版),2013,33(3):48-54.
(责任编辑 张淑艳)
Estimation formulas of vibration fundamental frequency based on asymmetry suspension bridge
YANG Guojun1, HAO Xianwu2, SONG Tao2, LI Ziqing2
(1.School of Civil Engineering, Lanzhou University of Technology, Lanzhou 730050, China; 2.School of Highway, Chang’an University, Xi’an 710064, China)
In order to calculate vibration fundamental frequencies of asymmetry suspension bridge conveniently and rapidly, frequency formulas for 1stvertical and torsional vibration of suspension bridge with asymmetric main cables were derived based on the Rayleigh’s method. As for 1stsymmetric vertical and torsional vibration, asymmetric structure influencing factors for the correction of code formula were put forward, and the formula for the crankle ratio of fundamental frequency was also derived. Finally, the accuracy of the proposed formulas was examined by the finite element method(FEM). The results show that 1stanti-symmetric vertical and torsional vibration of asymmetry suspension bridge is free from the influence of asymmetry structure parameter. While for 1stsymmetric vertical and torsional vibration, the decreasing range of fundamental frequency is obviously more significant when the structure sensitivity parameterξexceeds 0.1. The error between the fundamental frequency calculated by the proposed method and that by the FEM can meet the requirement of design phase, indicating that the proposed formulas can be applied to guiding the schematic design and preliminary design of asymmetry suspension bridge.
bridge engineering; asymmetry suspension bridge; fundamental frequency; Rayleigh’s method; estimation formula
2015-06-08;
2016-09-30
中央高校基本科研业务费专项资金资助项目(2013G1211010)
杨国俊(1988-),男,甘肃临夏人,博士,兰州理工大学讲师; 郝宪武(1962-),男,陕西绥德人,博士,长安大学教授,硕士生导师.
10.3969/j.issn.1003-5060.2016.11.020
U448.25
A
1003-5060(2016)11-1536-07

