基于灰数判断矩阵的Grey-AHP评估方法及其应用研究

瞿 浩

(合肥工业大学 管理学院,安徽 合肥 230009)



基于灰数判断矩阵的Grey-AHP评估方法及其应用研究

瞿 浩

(合肥工业大学 管理学院,安徽 合肥 230009)

文章利用灰色层次分析法(grey-analytic hierarchy process,Grey-AHP)构建了包括目标层、准则层和指标层3个层次的评价指标体系,对基于灰数判断矩阵的Grey-AHP评估方法进行研究,并通过一个具体案例的应用来验证文中所提方法的有效性。

层次分析法;灰区间数;判断矩阵;评估方法

0 引 言

层次分析法[1](analytic hierarchy process,AHP)是将与决策有关的元素分解成目标、准则、方案等层次,在此基础之上进行定性和定量分析的决策方法。AHP在应用中得到了较大改进和发展,但它的局限性也逐渐暴露。例如在建立模型时,它使用的是传统数学方法,处理的是“点数据”或“刚性数据”，而现实的社会经济系统则是柔性系统[2],所研究的问题多是柔性问题,用传统的数学方法描述未必有效。在管理工作中,由于信息不完备,人们做决策时往往会出现判断不确定的情况,用传统AHP处理不确定性问题显然是不合适的。

随着灰数理论[3]的完善,层次分析法与灰数理论结合应用的灰色层次分析法近年来在决策理论研究中取得了较为丰富的成果。文献[4]利用特征向量法求解灰色区间关联系数,避免了灰色决策中的权重确定;文献[5]构建了一类基于区间灰数信息的广义关联度模型;文献[6]设计了区间灰数加减逆运算的信息还原算子,提出了基于信息还原算子的区间灰数序列关联度的计算方法。但是,在现有研究中利用灰数理论构造具有灰数判断矩阵的层次分析模型的研究相对较少,而对于具有多个评价指标的不确定性问题的决策与评估又是社会经济系统一个十分重要的研究问题,鉴于此,本文提出基于灰数判断矩阵的Grey-AHP模型评估方法,并通过一个具体的社会系统柔性典型案例进行验证,从而体现该方法的有效性。

1 基于灰数判断矩阵的Grey-AHP模型

1.1 预备知识[7]

定义1 本文把只知道大概范围而不知其确切值的数称为灰数,用记号⊗表示。

定义3 令+、-、×、÷表示加、减、乘、除4种运算,则灰数⊗a,⊗b满足如下运算规律:

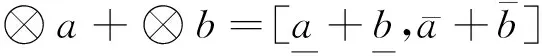
(1)

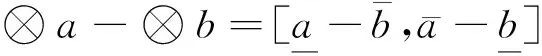
(2)

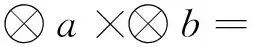
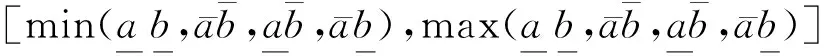
(3)

(4)

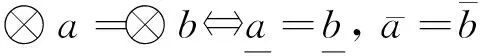
(5)

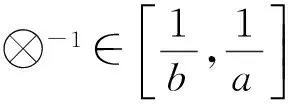
定义5 含有灰元素的矩阵称为灰色矩阵,记为A(⊗),并用⊗ij或⊗(i,j)表示灰色矩阵中第i行、第j列处的灰数。

定义6 设灰数矩阵D(⊗)=[⊗ij]m×n,M(⊗)=[⊗ij′]m×n,则如下运算规律成立:

(6)

(7)

(8)

(9)

1.2 模型的构建

在评估的过程中,决策者有时难以对某一个指标用一个精确的数值进行评估,采用Grey-AHP模型可以将此指标的评估值限定在一个相对的范围之内,从而更加真实地反映决策者的判断结果,并给出更贴近现实的评价指标偏重结论。

设D(⊗)=[⊗ij]m×n为灰数矩阵,相应的灰数权向量为w(⊗)=(w1(⊗),w2(⊗),…,wn(⊗))T,在一致的情形下,⊗ij=wi/wj(i,j=1,2,…,n),即w(⊗)为D(⊗)属于λ=tr(D)的一个特征向量。

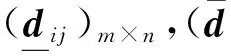
(10)

证明 由D(⊗)的一致性知,对j=1,2,…,n有：

(11)

由⊗ij=wi/wj(i,j=1,2,…,n)可得:

(12)

故得:

且

(13)

由(12)式可知 (10)式成立。

考虑到Ω的表达式,可得分数p、q分别为:

(14)

则Grey-AHP模型的建模步骤如下:

(1) 建立灰数判断矩阵。

(3) 确定参数p、q,规范化权重向量。

(4) 对指标进行权重排名，即对评价指标按照各自的权重值进行排序。

2 案例分析

本文以合肥工业大学管理学院2014届本科毕业生就业情况为例,构建就业竞争力评价指标体系,利用基于灰数判断矩阵的Grey-AHP模型对影响毕业生就业的因素进行定量评估,一方面验证本文所提方法对解决社会柔性问题的有效性,同时本文结果能够指导大学生合理定位就业导向,提高就业成功率。

2.1 案例准备

2.1.1 评价指标结构层次模型的建立

采用德尔菲法分别邀请相关专家对高等学校大学生就业竞争力的评价指标进行了诊断,具体步骤包括拟定意见征询表、确定征询对象、开展访谈及确定指标等。从研究目标出发,通过查阅相关文献资料,选取了15位高等院校学生管理工作者进行访谈,确定高等院校大学生就业竞争力的12项基本指标。按照指标体系的构建原则,结合专家建议,将评价指标分为3个层次:最高层,即目标层,指就业竞争力;中间层,即准则层,包括学校因素、自身因素与社会因素;最下层,即方案层,包含了12项相关的基本指标。高等院校大学生就业竞争力的评价指标层次示意图如图1所示。

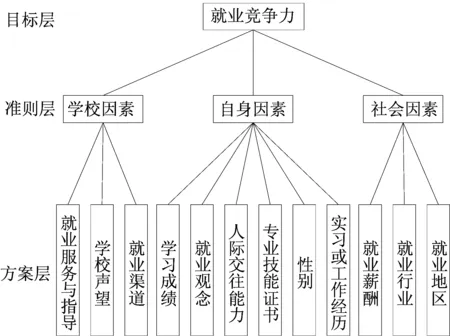
图1 大学生就业竞争力的评价指标层次示意图

2.1.2 指标分析

一个完整的高校毕业生就业竞争力评价体系应该从学校、个人、社会3个维度全方位构建而成。从学校维度上看,高校作为培养大学生、为社会输送人才的重要场所,应加强对大学生就业指导和职业规划,培养具有较强竞争力的大学生,符合市场的需求和用人单位的要求。本文在此维度下,选取的指标有就业服务与指导、学校声望、就业渠道;从个人维度上看,严峻的就业形势给大学毕业生带来的就业压力与日俱增,克服就业观念错位与就业能力不足可以改变当前大学生的就业现状。本文在此维度下,选取的指标有学习成绩、就业观念、人际交往能力、专业技能证书、性别、实习或工作经历;从社会维度上看,城乡发展的不平衡和薪酬、福利的不平等,再加上国家政策的城市导向和体制内导向,造成了大学生城市就业难、体制内就业难和高薪就业难的现状。本文在此维度下,选取的指标有就业薪酬、就业行业、就业地区。

2.1.3 数据来源

本文构建的高等院校大学生就业竞争力的评价指标体系模型包括学校因素、个人因素和社会因素3个方面,共12个指标。研究的对象为合肥工业大学管理学院2014届本科毕业生,各指标的得分均是通过精确的问卷调查与访谈,由该校长期担任学生管理工作、就业指导工作以及第一线的学生辅导员完成。数据来源方面真实、可靠,能够在一定程度上真实反映就业竞争力评价指标体系各指标的重要程度。

2.2 案例求解

在进行案例求解之前,本文对AHP的1-9标度进行灰数化划分。划分依据与1-9标度法相同[8],不同在于以区间灰数形式对应描述1-9标度中的标度值。1-9灰数标度划分标准定义见表1所列。

表1 AHP的1-9标度的灰数划分

由图1可知,合肥工业大学管理学院大学生就业竞争力的评价指标体系分为目标层、准则层和方案层3层。目标层即为本文的最终评价目标——大学生就业竞争力,准则层是开展大学生就业竞争力评估的3个方面,分别从学校、大学生自身以及社会3个方面对大学生就业竞争力进行具体评估。在学校因素方面,本文选取就业服务与指导、学校声望、就业渠道3个判断方案。就业服务与指导工作越得力,此项方案的得分就越高,反之就越低;学校的声望越好,此项方案的得分越高,反之其得分就会降低; 就业渠道越宽,该项方案相应的得分会越高,反之会降低。在大学生自身因素方面,本文选取6个判断方案:学习成绩、人际交往能力、专业技能证书、性别、实习和工作经历。一般来说,毕业生的学习成绩越好、人际交往能力越强,方案的得分就会越高,反之会降低。专业技能证书的获取以及是否具有实习或工作能力两项方案与得分值也保持正相关关系。对于性别,就近年来合肥工业大学管理学院大学生就业情况来看,性别不同,其就业竞争力的确有所区别。一般情况下,男生的就业竞争力相对高于女生的就业竞争力,但该情形有逐渐降低的趋势。在社会因素方面,本文选取就业薪酬、就业行业、就业地区3个判断方案。一般来说,毕业生对就业薪酬要求越高,就业行业选择得越热门,就业地区选择得越发达,该方案的得分就越低,反之会升高,即社会因素中的3个方案与就业竞争力得分呈现负相关关系。通过对图1中3个准则进行两两比较,其结果见表2所列。

表2 准则层两两比较结果

本文对判断矩阵进行一致性检验。首先将灰数判断矩阵进行拆分，即

针对判断矩阵M1、M2,一致性检验结果见表3所列，表3中，RI为随机一致性指标；CI为置信区间。

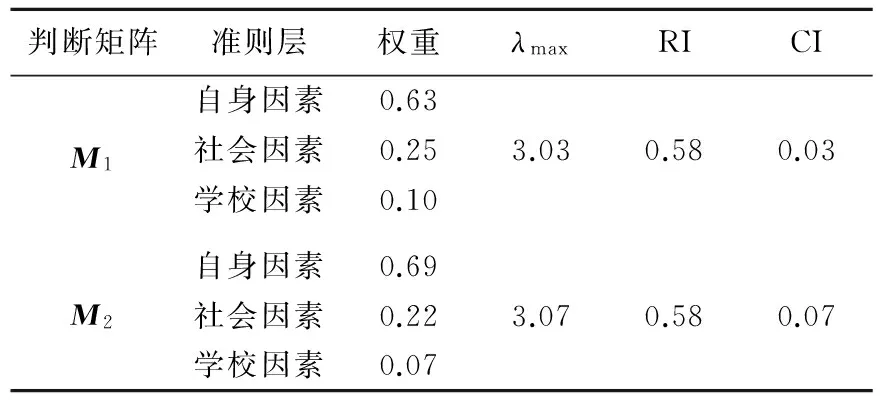
表3 判断矩阵M1、M2的一致性检验结果

由于表3中的指标CI值(CI<0.1)满足一致性要求,故灰色判断矩阵具有一致性。

本文将基于Grey-AHP模型对影响大学生就业竞争力的12项指标进行两两比较,见表4所列。

表4 就业竞争力指标的得分与权重排名

由表4可知,合肥工业大学管理学院2014届毕业生在就业地区的选择、实习或工作经历、人际交往能力等3项指标的权重得分占据着就业竞争力排名的前3位,而专业技能证书、就业薪酬、就业服务与指导3项指标居于就业竞争力排名的最后3位。其他6项指标占据着排名的第4至第9位。

4 结 论

本文结论与在访谈时所获意向性结论基本相同,与全国高等院校毕业生就业竞争力分析的大趋势也保持较高程度上的相似性。结果表明，我校毕业生的就业能力与全国其他高校毕业生就业能力的平均情况基本一致,同时也证明了本文给出的基于灰数判断矩阵的Grey-AHP模型在对以就业竞争力评估为例的社会系统中柔性问题进行定量评估分析时的有效性。

[1] SAATY T L.Fundamentals of decision making and priority theory:analytic hierarchy process[M].Pittsburgh:RWS Publications,2006.

[2] 吴育华,诸为,李新全.区间层次分析法:IAHP[J].天津大学学报,1995,28(5):700-705.

[3] 刘思峰,党耀国,方志耕,等.灰色系统理论及其应用[M].5版.北京:科学出版社,2010.

[4] 罗党.灰色决策问题的特征向量法[J].系统工程理论与实践,2005,25(4):67-71.

[5] XIE Naiming,ZHENG Jing,XIN Jianghui.Novel generalized grey inidence model based on interval grey numbers[J].Transactions of Nanjing University of Aeronautics & Astronautics,2012,29(2):118-124.

[6] 杨保华,方志耕，周伟，等.基于信息还原算子的多指标区间灰数关联决策模型[J].控制与决策,2012,27(2):182-186.

[7] LIU S F,LIN Y.An introduction to grey system: foundation,methodology and applications[M].IIGSS Academic Publisher,1998:13-24.

[8] SAATY T L.Mathematical principles of decision making[M].Pittsburgh:RWS Publications,2010.

(责任编辑 万伦来)

Research on Grey-AHP assessment method based on grey number judgment matrix and its applications

QU Hao

(School of Management, Hefei University of Technology, Hefei 230009， China)

By using the grey-analytic hierarchy process(Grey-AHP) assessment method to construct the assessment index system with three levels of target, guideline and index, the Grey-AHP model based on the grey number judgment matrix is studied. The effectiveness of the proposed method is verified by a specific example.

analytic hierarchy process(AHP); grey interval number; judgment matrix; assessment method

2015-11-26；

2016-07-07

瞿 浩(1973-),男,上海市人,博士,合肥工业大学讲师.

10.3969/j.issn.1003-5060.2016.11.025

G647

A

1003-5060(2016)11-1567-04