基于非对称联系云的软土沉降等级评价模型

朱其坤, 汪明武, 李亚峰, 赵奎元, 金菊良

(合肥工业大学 土木与水利工程学院,安徽 合肥 230009)



基于非对称联系云的软土沉降等级评价模型

朱其坤, 汪明武, 李亚峰, 赵奎元, 金菊良

(合肥工业大学 土木与水利工程学院,安徽 合肥 230009)

软土沉降等级评价受诸多边界模糊的、有限区间分布的不确定因素影响。文章基于集对论和云理论,提出一种能考虑指标区间边界模糊和非对称特点的土体沉降等级联系云评价新模型,即首先构建基于集对同异反分析的非对称联系云模型,以非对称定量统一描述软土沉降等级评价指标的模糊性及在分类间的转换态势,并结合指标权重综合分析样本与沉降等级间的确定度,以确定土体沉降等级。实例应用结果与现场观测结论及可拓评价结果的对比分析表明,该模型应用于软土沉降等级划分是有效可行的,且克服了传统云模型局限于指标为正态分布的缺陷。

软土;沉降;非对称联系云;集对;确定度

0 引 言

随着城市化进程的加快,土地资源已日益紧缺,促使人们将大量工程建设于软土场地上,特别是我国沿海地区[1],而软土具有流变、变形大和触变性特点,且沉降稳定历时较长,若对其沉降等级认定不当,导致设计和工程措施不合理,往往会造成构筑物大变形和倾斜及生命线工程破坏,甚至工程灾害和人员伤亡[2-3],故对软土施工前的沉降等级进行准确合理的定性评价,对区域规划、工程基础设计和施工方案制定具有重要实际意义。然而,据已有文献报道,以往人们对土体沉降的研究主要集中在工后沉降量的预测方面,并提出了双曲线法、三点法、灰色理论法、泊松曲线法和图解法等,但这些预测方法必须以工后的地基实测沉降数据为基础,显然不能应用于设计和施工前沉降等级的定性评价和划分。另外,软土沉降等级评价指标具有模糊性和有限区间分布特点,且不一定服从正态分布,导致目前对土体沉降分级研究的文献很少[4]。

鉴于软土沉降等级评价指标常呈现出一定区间内的模糊性和随机性特征,且实测指标值隶属于某等级存在确定和不确定性及转换特点,本文尝试将集对论和云模型耦合起来构建非对称联系云分析模型,并应用于软土沉降等级的评价,以统一定量分析实测指标的局限分布和在不同等级间的转化态势对分类结果的影响,提高软土沉降等级划分的可靠性。

1 非对称联系云评价模型

1.1 非对称联系云基本概念

云模型是由中国工程院院士李德毅提出[5-6],能够实现对概念语言以定量方式描述客观事物的不确定性,现已广泛应用于工程界中定性概念存在的模糊性和随机性问题分析。然而,传统云模型等级分类中,生成指标等级云一般为理想的无限区间正态云,没有考虑指标值分布的有限区间性,且不能给出结果与相邻等级区间的转化关系,故传统云模型虽解决了不确定性问题的随机性和模糊性,但忽视了各等级之间的联系和指标实际分布形式,而这可能导致结果与实际情况存在偏差,不利于实际应用。

由上述分析可知,应用传统云模型可反映软土沉降等级的模糊性和随机性特性,但计算分析要求评价指标为正态分布形式,然而实际指标分布形式可能不能满足这一要求,加上传统云模型模拟中无法分析指标值在某相邻等级间的转化态势,故在软土沉降等级评价中若采用传统正态云模型反映指标的随机性和模糊性特性必然与实际的软土现场情况存在差别。而近期发展起来的集对论则在统一刻画确定和不确定性态势转换方面具有优势[7],也为克服传统云模型的缺陷提供了思路。

因此,本文据实测指标分布的实际情况,引入集对论对有限区间云模型模拟进行控制和改进,并提出非对称联系云模型,以真实反映软土沉降评价指标的分布特点和实现指标与评价等级间的确定和不确定关系的统一辩证定量描述。

(1)

(2)

(3)

(4)

(5)

由以上分析可知,联系云模拟的核心是分析实测值与评价等级标准间的关系,即半区间长度确定及分析。根据集对分析同异反原理[8-10],在云生成过程中,将实测指标与指标j的第i等级的同异反准则定义如下:当实测指标值位于标准等级i区间内,为同一关系;位于相邻等级内(等级i-1或i+1内),则两者为异关系;位于其他等级内则为对立关系。故等级i的联系云半区间长度ai左和ai右由同一关系区间的一部分和差异关系区间组成。当评价指标分类标准等级区间值随着等级的增大而单调增加时,则等级i的左、右半区间长度为:

(6)

当评价指标分类标准等级区间值随着等级的增大而单调减小时,等级i的左、右半区间长度为:

(7)

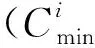
(8)

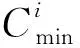
1.2 基于非对称联系云的评价流程

基于非对称联系云模型的软土沉降等级评价基本原理为:首先根据评价指标标准计算每一稳定级别的左半区间长度a左和右半区间长度a右,进而求出与左、右半区间长度相对应的非对称联系云左半支和右半支的数字特征(Ex,En,He,a,k);再根据所求出的非对称联系云的左、右半支的数字特征生成相应有限区间内的随机数,并模拟评价指标隶属于某沉降等级的云模型;最后根据样本指标实测值计算其属于土体各沉降等级的确定度,并结合指标综合权重求得综合确定度,以综合判断样本的级别。

1.3 非对称联系云评价模型

对于软土沉降等级评价问题,非对称联系云的生成还应结合等级特点,中间等级的非对称联系云(i=2, 3,…,m-1对应的云)和两端等级云(i=1,m对应的云)形态有明显区别,两端等级云中远离中间等级云的1/2范围实际分布并不为正态分布,而是确定度为1的均匀分布,故相应的确定度计算模型不同。对于中间云,基于非对称联系云概念计算样本p的第j指标的指标值y0属于等级i的确定度时,当评价指标值y0在中间云和两端云的靠近中间云的1/2范围内,指标j的指标值y0属于i等级的确定度为μp,ij,计算公式为:

(9)

当评价指标值y0在两端等级云的远离中间云的1/2范围内,不应为正态分布而应为确定度为1的均匀分布。

基于上面求得的各指标值隶属于各等级云的确定度,再结合评价指标的权重可计算样本p属于等级i的综合确定度μp,i:

(10)

其中,μp,ij为样本p的第j指标的样本值属于等级i的确定度;λp,j为样本p评价指标j的权重。根据综合确定度的值,按最大隶属原则即可判定样本p所属的等级k，即

(11)

2 实例应用

为了验证本文模型的有效性和适用性,采用文献[4]中的实例数据进行验证和对比分析。实例中的土体沉降等级划分选取了软土层的埋深H、厚度h、孔隙比e、液性指数IL和压缩模量Es共5个指标作为土体沉降的评价指标,地基土土体沉降分为5个等级,即轻微沉降Ⅰ、较小沉降Ⅱ、中等沉降Ⅲ、较大沉降Ⅳ、严重沉降Ⅴ,相应的分类标准和样本实测值[4]见表1、表2所列。

基于本文的模型,根据土体沉降评价指标分类标准的各等级区间值,由(2)～(8)式可计算出评价指标对应等级的联系云数字特征(Ex,En,He,a,k),再根据(1)式模拟指标j属于等级i(i=1,2,…,5)左半区间和右半区间的各2 000个云滴,即可构成评价指标j对应等级i的联系云,如图1所示。图1a～图1d中从左到右分别为指标等级Ⅰ到Ⅴ的联系云,而图1e中从左到右分别为等级Ⅴ到Ⅰ对应的联系云。

表1 沉降等级评价指标分类标准

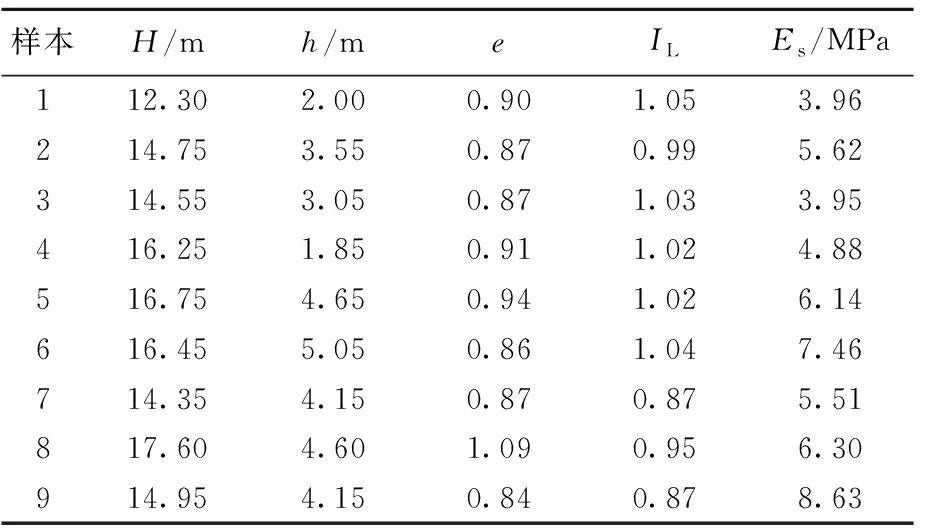
表2 钻孔样本实测值

为方便与可拓方法的计算结果进行对比分析,权重采用与文献[4]中相同的权重集,即λp,j={0.113,0.271,0.156,0.109,0.353},实例的土体沉降等级评价结果见表3所列。

图1 评价指标等级的非对称联系云

样本综合确定度μ(Ⅰ)μ(Ⅱ)μ(Ⅲ)μ(Ⅳ)μ(Ⅴ)本文评价结果10.1650.2210.0880.2060.386Ⅴ200.0140.6230.4340.025Ⅲ300.1290.4070.1500.356Ⅴ40.1940.0820.1630.4210.212Ⅳ5000.2770.7040.031Ⅳ60.0440.3520.1890.3400.160Ⅱ70.0170.1270.3350.5910.048Ⅳ800.0050.4270.4130.205Ⅲ900.1140.3630.2080Ⅲ

现以样本1中的指标1即软土层埋深(y0=12.30)为例,阐述其对等级Ⅰ～Ⅴ的确定度计算过程。由(9)式计算得到μ1,11=0.303,μ1,21=0.716,μ1,31=μ1,41=μ1,51=0,表明软土层埋深y0=12.30隶属于沉降等级Ⅱ的程度最大，其次隶属于等级Ⅰ,不可能隶属于等级Ⅲ、Ⅳ及Ⅴ。同理可求出其他指标属于各个等级的确定度,然后结合指标权重通过(10)式即可求得样本属于不同等级的综合确定度,由(11)式得出的最大综合确定度值所对应的级别即为样本的稳定性级别。

由表3可知,样本1和样本3属于等级Ⅴ,样本2、样本8和样本9属于等级Ⅲ,样本4、样本5和样本7属于等级Ⅳ,样本6属于等级Ⅱ。本文基于非对称联系云模型评价结果与文献[4]可拓评价结果和现场观测结果一致,表明非对称联系云模型应用于软土沉降等级评价是有效可行的;同时,综合反映了实例软土指标的模糊性、随机性和实际分布特征,在等级划分时避免遗漏重要约束条件和传统云模型局限于指标为正态分布的弊端。

由此可见,非对称联系云软土等级评价过程中可实现定性定量之间转换,且应用集对分析中同异反原理将无限正态区间变为有限区间,此外,分析中考虑了模拟值在等级区间之间的相互转换态势,可补充以往云模型不能反映的信息,使评价结果与实际情况更加相符,为城市的规划、工程设计提供了依据。

3 结 论

软土沉降等级评价受诸多不确定性因素影响,是一个极其复杂的问题。本文构建了基于非对称有限区间联系云模型的软土沉降等级评价方法,并应用于实际工程,与可拓方法进行对比分析,结果表明该模拟应用于软土沉降等级评价是有效可行的,在评价过程中可实现定量描述等级之间的模糊转换态势,能充分反映评价指标值实际分布情况,并综合定量考虑指标隶属于不同等级的确定和不确定性,克服了传统云模型对数据分布形式要求严格的缺陷。本文模型可为其他类似评价问题提供一种参考。

[1] 简文彬,吴振祥,刘慧明,等.闽东南沿海地区软土静力触探参数相关分析[J].岩土力学,2005,26(5):733-738.

[2] 滕延京,王曙光.新《建筑地基基础设计规范》解读[J].标准规范,2012,30(12):1-6.

[3] 刘念武,龚晓南,楼春晖.软土地区基坑开挖对周边设施的变形特性影响[J].浙江大学学报(工学版),2014,48(7):1141-1147.

[4] 盛渊,王清,孙涛,等.天津滨海新区地基土工程地质分区的可拓学评价[J].东北大学学报(自然科学版),2014,35(12):1502-1506.

[5] 李德毅,孟海军,史雪梅.隶属云和隶属云发生器[J].计算机研究和发展,1995,32(6):16-21.

[6] LI Deyi,HAN Jiawei,SHI Xuemei,et al.Knowledge representation and discovery based on linguistic atoms[J].Knowledge-Based Systems,1998,10(7):431-440.

[7] 沈时兴,金菊良,宋松柏,等.水文水资源集对分析的理论基础探讨[J].合肥工业大学学报(自然科学版),2013,36(12):1481-1488.

[8] 汪明武,金菊良,周玉良.集对分析耦合方法与应用[M].北京:科学出版社,2014:38-55.

[9] 杜德平,应国柱.基于层次分析和集对分析的地铁施工风险评估[J].合肥工业大学学报(自然科学版),2014,37(8):962-965.

[10] WANG Mingwu,XU Peng,LI Jian,et al.A novel set pair analysis method based on variable weights for liquefaction evaluation[J].Natural Hazards,2014,70(2):1527-1534.

(责任编辑 张淑艳)

A novel settlement grade evaluation model for soft clay based on asymmetric connection cloud

ZHU Qikun, WANG Mingwu, LI Yafeng, ZHAO Kuiyuan, JIN Juliang

(School of Civil and Hydraulic Engineering, Hefei University of Technology, Hefei 230009, China)

Indices distribution of settlement grade evaluation for the soft clay presents uncertainty of boundary fuzziness in the finite interval and interaction among various classifications. So a novel coupled connection cloud model using the set pair theory and cloud theory is introduced to classify the settlement grade of soft clay. In this model, the asymmetric connection cloud model using the identity-discrepancy-contrary(IDC) principle of set pair analysis is established to interpret the evaluation indices’ fuzziness, asymmetry and transformation state among index intervals. Based on the index weight and the measured value, the certainty degree to each grade is calculated to generate the comprehensive certainty degree to the certain grade, and then the settlement grade of the sample is specified. Finally, the comparison of the results of a practical example with those of the extension evaluation and field observations shows that the proposed model is feasible and effective, and can overcome the crucial restriction of the conventional cloud model that the index must obey normal distribution.

soft clay; settlement; asymmetric connection cloud; set pair; certainty degree

2015-07-09

国家自然科学基金资助项目(41172274;71273081)

朱其坤(1990-)，男，安徽泗县人，合肥工业大学硕士生； 汪明武(1972-)，男，安徽歙县人，博士，合肥工业大学教授，博士生导师； 金菊良(1966-)，男，江苏吴江人，博士，合肥工业大学教授，博士生导师.

10.3969/j.issn.1003-5060.2016.11.016

TU447

A

1003-5060(2016)11-1515-05