转向主销定位参数和接地点偏距的解析研究

杨一洋，谢敏松

（泛亚汽车技术中心有限公司，上海 200135）

前言

车轮转向主销定位参数对车辆运动的力学稳定性起着至关重要的作用［1-2］。主销的定位角有利于减少转向操纵力、减少回跳与跑偏现象、改善车辆直线行驶的稳定性。主销的偏置距影响轮胎力对转向瞬时中心的力矩，对车辆的回正性能和直线行驶性能具有重要影响［3-5］。合理的主销定位也会改善轮胎的偏磨，延长轮胎的寿命［6］。

对车轮定轴转向运动的悬架而言，主销轴固定不动［7-9］。麦弗逊和双横臂悬架都属于轮毂定轴转向悬架。而对于多连杆悬架，其虚拟主销在转向过程中时刻发生改变，难以采用传统的空间运动解算方法［9］。另外，通常情况下整车仿真采用零度转向下的主销参数来代替实际转向的情况，这也是部分由于有些K&C台架（悬架运动学和弹性动力学测试台架简称）对主销解算精度甚至解算能力的不足导致的。

为此，本文中提出车轮转向主销参数及其接地偏置距的解析方法，它适合于不同车型，包含车轮定轴运动的悬架和虚拟主销悬架的车辆。首先分析了车轮微小转动前后的车轮定位矢量，根据空间旋转的变化矩阵，并通过误差修正迭代求解出满足误差阈值的主销定位参数。并选取某两辆不同类型车辆进行验证，实车的数据与解析计算结果基本吻合，表明了推导的车轮转向主销参数和接地点偏置距解析的准确性，且该解析算法可连续表达各转向角度下的主销参数。

1 车轮转向主销运动解析

主销是传统汽车上转向轮转向时的回转中心，是一根销轴，如图1左所示。但目前许多独立悬架的汽车已不存在真实主销，如图1右所示。图1左为传统的麦弗逊悬架，悬架主销轴为上衬套点A与下球铰点B的连线；图1右为一种多连杆系统，两个上控制臂连线的交点C与下控制臂连线的交点D的连线构成转向主销的轴线，随着车轮转向，主销定位参数发生变化，为一种虚拟销轴的形式［6］。

图1 两种典型悬架形式的转向主销轴示意图分析

对主销参数的求解，通常采用K&C台架进行分析，例如，MTS台架用于采集悬架行程、轮胎轮心位移和转向角度与力矩等信息［7-8］。

1.1 主销的角度计算解析

前轮定位的空间几何关系如图2所示，图中O为轮胎接地印迹中心，C为轮心，B为主销M轴线与地面的交点，下称主销接地点。τ和σ分别为主销的后倾角和内倾角，δ为车轮的转向角。正常车轮转向时，车轮轮胎绕主销轴转动。车轮的法向量N1也会随之绕主销轴M转动。

另车轮平面法向量为N1(x c N1，y c N1，z c N1)，可知车轮法向量N1在XO Y平面的投影(x c N1，y c N1，0)与X0轴(1，0，0)的夹角为δ+90°。

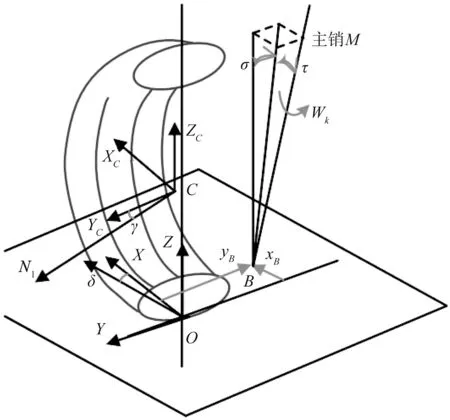
图2 前轮定位的空间几何关系图

车轮法向量N1(x c N1，y c N1，z c N1)与Z轴(0，0，1)的夹角为外倾角γ加上90°。同理可知

简化处理，令ycN1=1，经演化得

车轮法向量N1的单位向量为

若此时车轮转动微小角度θ，车轮将会绕主销转动到新的位置，同理可求出新位置车轮N2向量。

将其转化为已知空间两向量1到向量2和转动的角度θ，求其旋转轴的数学问题。举例如图3所示，原向量1为(0，2 2，2 2)，轴向量为Y轴（0，1，0），若绕轴向量旋转90°，易知新位置向量2在X0Y面上，为( 2 2， 2 2，0)。同时旋转后新位置是唯一的。同理，若已知原向量和旋转后的新向量以及旋转角度，则轴向量也是可求解的。

本文中通过假设迭代方案，通过空间转动变化矩阵的方法辨识出主销定位参数。首先已知主销初始向量M(-tanτ1，-tanσ1，1)，其中，τ和σ分别为主销的后倾角和内倾角，求出围绕主销转动微小角度θ的变换矩阵，然后通过变换矩阵求解出转动后的新矩阵。这里采用文献的变换矩阵的推导［10］，也可采用Matlab自带Makehgtform函数求出变换矩阵。

图3 空间定轴旋转

将转动后的向量N20与向量N2点乘以判断两向量的重合误差：

若ER D越大，即越接近1，两向量重合度越高。根据误差，修正主销值，然后再进行误差判断迭代，直至误差满足一定阈值ξ。

式中f为主销参数值修正函数。通过迭代求解出满足误差阈值的主销角度定位参数τ和σ。

1.2 主销接地点与轮胎印迹中心偏置距的解析

如图2所示，主销接地点B(x B，y B，z B)与轮心C点的向量B C也同理符合上述绕轴运动的规律。可知主销接地点与轮胎印迹中心O共面，均在X O Y平面内，BC向量为

绕主销转动θ角度到新位置，同上通过迭代求解出满足误差阈值ξ2的主销接地点B(x B，y B，0)。

图4 为主销接地点B平面坐标转换示意图，点B在大地X OY平面坐标系的x坐标xB和y坐标yB分别称主销的纵向与横向偏置，而轮胎逆时针转动一个角度δ后，B点在与轮胎固结的X1O Y1坐标系的x坐标x1B和y坐标y1 B则分别称为主销纵偏距与侧偏距。

根据图4中的几何关系，不难得出新老两组坐标的关系式：

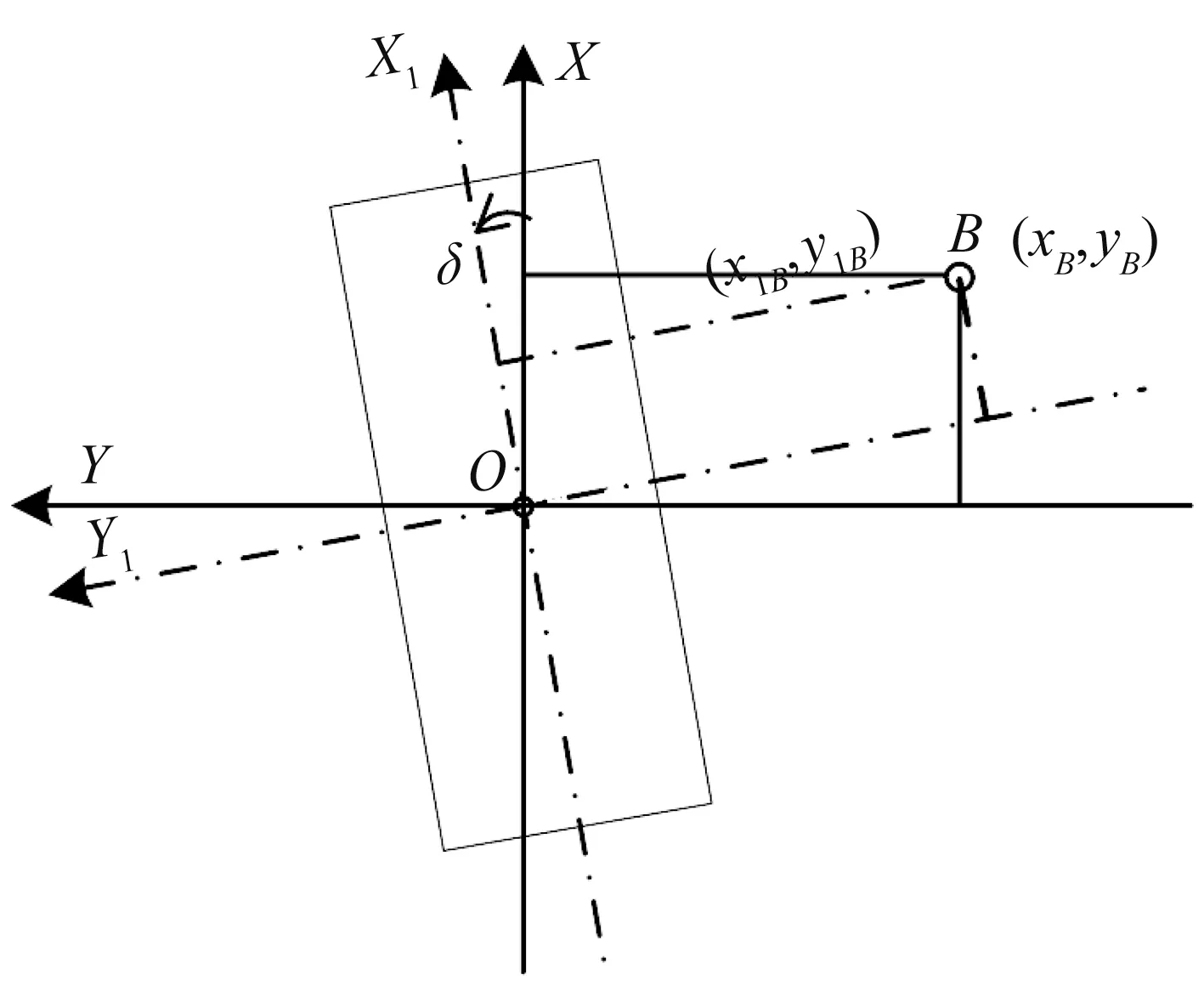
图4 主销接地点B坐标转换示意图

2 基于K&C实车主销解算和验证

本文中选取某两汽车厂家不同悬架型式的车辆进行解算和验证，包含某麦弗逊悬架车辆A和某多连杆悬架车辆B。首先从K&C试验台架数据获取测量信息，然后通过式（1）~式（13）算出主销各定位参数。图5~图9为某麦弗逊悬架车辆（A车）的主销定位角度和主销侧、纵偏矩随转向盘转角而变化的曲线。

图5 车辆A主销内倾角-转向盘转角曲线

图6 车辆A主销后倾角-转向盘转角曲线

图7 车辆A轮胎接地印迹中心轨迹和主销接地点

图8 车辆A主销侧偏距-转向盘转角曲线

图9 车辆A主销纵偏距-转向盘转角曲线

从图5和图6可以看出，装麦弗逊悬架的车辆，其主销的定位角几乎不随转向盘转角而变化。图中曲线的微小斜率是由于实车测试中，车辆橡胶衬套和铰接处间隙导致的微小变化。由图7可看出，随着转向盘转角的变化，轮胎接地印迹中心画出一条轨迹，而主销接地点基本不变。由图8和图9可知，主销侧偏距也基本不变，而纵偏距则有所变化，对车辆回正有所影响。

图10 ~图14为装有多连杆悬架某车辆（B车）虚拟主销的定位角和主销侧、纵偏距随转向盘转角而变化的曲线。

图10 车辆B主销内倾角-转向盘转角曲线

图11 车辆B主销后倾角-转向盘转角曲线

图12 车辆B轮胎接地印迹和主销接地点轨迹

从图10~图14可以看出，该多连杆悬架车辆B的主销定位角度、主销接地点和主销侧偏距与纵偏距都随着转向盘转角而变化。另外，从图12中还可看出，轮胎接地印迹中心轨迹末端有错动现象，可能是大角度转向下衬套或弹性体错动导致的。若利用之前文献方法来处理，结果会有局限性。通过本文解析算法与辨识，可较准确地求解主销随转向盘转角的变化趋势。

图13 车辆B主销侧偏距随转向曲线

图14 车辆B主销纵偏距-转向盘转角曲线

将转向盘转角为零时计算出的主销定位角的解析值与其实车值进行对比，结果如表1所示。

表1 整车主销定位角解析值与实车值的对比

表中主销定位角的实车值是指厂家的设计目标值，一般允差为±0.6°。对于麦弗逊悬架车辆A而言，本文同时对该车在四轮定位设备上进行四轮参数验证，四轮定位测试的主销内倾角和后倾角分别为14.3°和3.7°。结果有较高的一致性。

3 结论

本文中提出一种新的车轮转向主销的定位角和接地点侧、纵偏距的解析方法，适合于不同车型，包含车轮绕轴运动的悬架和虚拟主销悬架的车辆。将两款有代表的车辆进行K&C解算与实车值对比，结果表明该解析法能准确表达两种悬架性能趋势，且具有较高精度。

（1）提出车轮转向主销的定位角和接地点侧、纵偏距的解析方法，通过实车台架验证，证明了解析方案的准确性，且可连续表达转向盘各转角下的主销参数。

（2）本文的解析算法也准确验证了车轮定轴转向悬架和虚拟主销悬架的定位差异。为整车仿真主销参数变化曲线提供途径，同时完善和更新了悬架K&C的数据库。