基于微分博弈的乳制品供应链质量协调机制分析

□ 郑红越　南京财经大学

基于微分博弈的乳制品供应链质量协调机制分析

□ 郑红越南京财经大学

本文的研究对象是以乳企为核心企业的两级供应链。其中，乳企（m）控制乳制品加工和乳制品保鲜，奶站（s）控制原奶质量检测和乳制品保鲜。为确保乳制品最终的质量，核心企业（乳企）应站在全局的系统的角度对奶站进行供应链质量管理的协调。

基本假设

①奶站的质量管理活动包括质量检验（Is）和温度控制（Ts），乳企的质量管理活动包括加工（Pm）、温度控制（Tm）。其中，Is、Ts、Tm只能维持乳制品的质量，是质量控制活动；Pm能够改善乳制品的口味，是质量改进活动。

②消费者购买乳制品质量的提升乳企的加工水平的努力水平决定。用公式（1）微分方程描述乳制品质量的动态变化规律：

其中

Q(t)表示在t时刻的乳制品质量；Q(0)=Q0：初始时刻的乳制品质量；α：乳企的加工水平对乳制品质量的影响系数；η：乳制品质量水平的退化率。

③假设供应链的收益函数与奶站和乳企的质量控制活动的努力程度线性相关，产品质量改进带来的收益函数与产品质量成正比，如公式（2）：

其中，λ、γ、φ：奶站和乳企各自的质量控制活动水平对收益函数的影响系数；δ：乳制品质量对供应链总收益的影响系数。

④奶站和乳企的质量努力成本函数为凸函数，假设奶站和乳企的成本函数为（2）：

其中，ki(i=1,2,3,4)：对应质量努力工作的成本系数。

⑤假设奶站获得的收益份额为θ，则乳企获得的收益份额为1-θ。假设奶站和乳企有相同且为正值的体现率ρ。

乳制品供应链质量行为博弈模型构建

双方独立平等Nash非合作博弈模型

奶站和乳企地位平等，独立承担各自质量成本，进行决策时，选择能实现各自利润最大化的最优质量行为。奶站和乳企进行相同的博弈，根据静态反馈N ash均衡的充分条件，奶站的最优值函数Vs和乳企的最优值函数Vm满足HJB（Ham ilton-Jacobi-Bellm an）方程，解HJB方程，得到奶站和乳企在双方独立平等时的静态反馈N ash均衡的解，如式（3）：

因此易求得，在N ash均衡下，乳制品供应链中奶站和乳企的最优值函数以及整个供应链的收益函数，如式（4）：

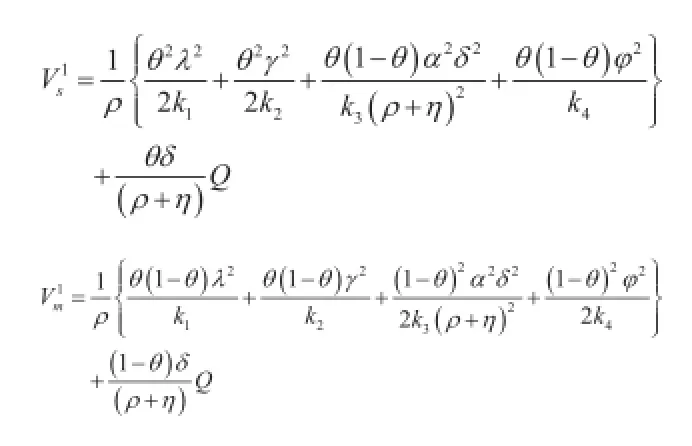
乳企激励政策下的Stackelberg博弈模型

当乳企处于主导地位，奶站作为追随者时，双方之间将进行Stackelberg博弈，乳企为激励奶站，主动承担奶站部分质量行为成本。博弈顺序如下：首先乳企决定自身的质量行为以及为奶站承担的质量成本分担系数ω∈（0,1）；然后奶站根据自身利润最大化原则决定自身的最优质量努力水平。利用逆向归纳法，首先确定奶站的最优质量努力水平。乳企将依据奶站的最优质量函数来确定自身的最优质量努力水平和质量成本分担系数，解HJB方程，得到奶站和乳企在乳企主导下的最优质量努力水平，如式（5）：

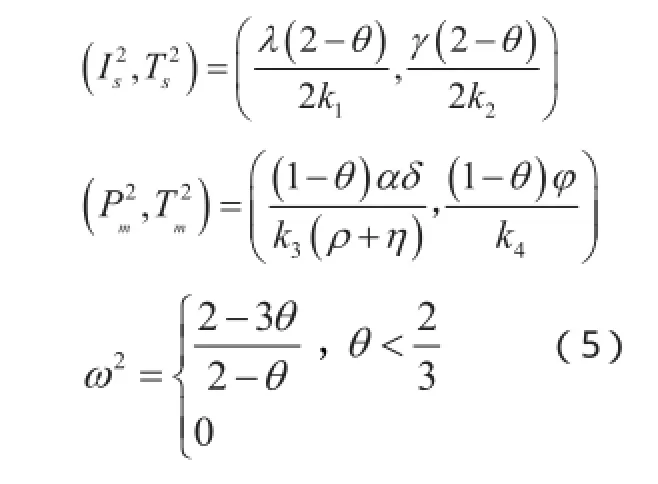
因此求得在Stackelberg均衡下，乳制品供应链的最优利润奶站和乳企的最优值函数，如式（6）：