略谈教师如何有效使用教材
——以沪科版八年级上册几何内容为例
汪洪潮(安徽省合肥市包河区教研室)
略谈教师如何有效使用教材
——以沪科版八年级上册几何内容为例
汪洪潮(安徽省合肥市包河区教研室)
数学课堂教学离不开教材,教材的编写凝聚着编者的智慧和心血,理解教材是用好教材的前提.怎样理解教材?如何用好教材?是一线教师首先要思考的问题.准确理解教材内容的编写体系,领悟数学概念的内涵和本质,抓住图形间的相互联系,深入挖掘例、习题的功能,可以有效地帮助教师准确把握教材,用好教材.
理解教材;编写意图;概念教学;用好教材
课堂教学离不开教材,任何一个版本的教材,都是专家按照《义务教育数学课程标准(2011年版)》(以下简称《标准》)的要求,按照一定的逻辑体系,精心编写而成.教材通过对章节内容的合理布局,知识点的科学阐述,例、习题的巧妙安排,系统而合理地落实《标准》对本学段的学习目标.作为一名教师,要教好数学,首先是要读懂教材、理解教材,然后再用好教材.曾有学者指出,许多教师举着“用教材教”的旗帜,在不研究教材、不钻研教材的情况下,大胆“创新”,既不准确理解教材编写者的意图,也不能准确地把握教学内容,以及教学重点、难点,冒然组织教学,大胆进行“变革”,这种现象确实令人叹息!
由于担任教研员工作,经常深入课堂听课,对此现象深有同感,现以沪科版《义务教育教科书·数学》(以下统称“沪科版教材”)八年级上册几何内容为例,略谈教师如何深刻理解教材,如何有效使用教材.
沪科版教材八年级上册几何部分共有三章,分别是第13章“三角形中的边角关系、命题与证明”、第14章“全等三角形”、第15章“轴对称图形与等腰三角形”.每一章中既有概念学习、性质探究等内容,又有巩固知识、形成能力、渗透思想方法的例、习题,更有培养空间观念、几何直观和逻辑推理能力的大量资源.对这些内容的教学,教师应该如何研读教材,才能有效实现《标准》的要求呢?
一、理解教材编写意图,把握章节内容结构
案例1:八年级上册第13章第1节中“三角形内角和定理”的部分内容.
在一个三角形中,三个内角之间有什么关系?
在小学,我们曾经用折叠(如图1)、剪拼(如图2)或用量角器度量的方法研究过这个问题.你还记得有什么结论吗?

图1
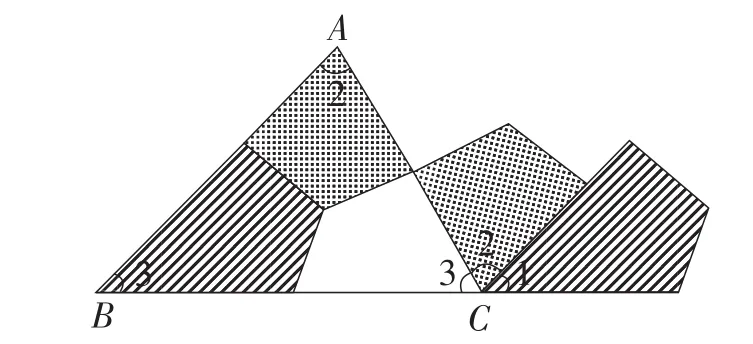
图2
得出结论:三角形内角和等于180°.
然后应用这个结论解题.
对于以上内容很多教师认为,可以先证明三角形内角和定理,再应用,不理解教材为什么将定理的证明安排在第2节“命题与证明”之后.
要理解教材的编排意图,必须先理解《标准》对几何部分的教学建议:对几何的学习,可以先通过画图、折纸、度量或做实验等活动,探索发现结论,然后再对结论进行说明、解释或证明.从七年级到八年级要循序渐进地培养学生的推理能力,做好由实验几何到论证几何的过渡.
教材正是按照《标准》的建议,先通过回忆、折叠等方法让学生对“三角形内角和为180°”有一个直观的认识,初步运用结论解决一些问题,再进行严格的证明.这样将实验几何与论证几何有机结合,突出先说理、再证明的几何学习两步走的方针.
理解教材还要把握内容的逻辑结构.教材对三角形相关内容的编排顺序是:(1)三角形的定义与基本构成元素(三条边、三个内角);(2)三角形的基本构成元素之间的关系;(3)三角形的基本类型与相应的判定和性质;(4)三角形之间的基本关系,以及相应处理方法等.这样编排既符合学生的认知发展水平,又符合知识间的逻辑顺序.
例如,教材将线段的垂直平分线、等腰三角形、角平分线的性质和判定都放在轴对称图形一节后面学习,正是抓住了它们都具有轴对称性的一般性质.
我们只有理解了教材的编写意图,把握了内容间的逻辑结构,才有可能理解教材,用好教材.
二、准确解读教材对概念的阐述,培养学生思维和概括能力
数学概念是数学知识的基石,是数学思想方法的载体,也是训练数学思维的有效工具.通过对数学概念的学习,把蕴含在概念中的数学思维活动打开,以若干典型具体事例为载体,引导学生展开分析各事例的属性、抽象概括共同本质属性、归纳得出数学概念等思维活动而获得概念.
案例2:第13章中有如下几个概念:
(1)由不在同一直线上的三条线段首尾依次相接所组成的封闭图形叫做三角形.
(2)三角形中,三个角都是锐角的三角形叫做锐角三角形;有一个角是直角的三角形叫做直角三角形;有一个角是钝角的三角形叫做钝角三角形.
本节中的有关概念,小学阶段就已经接触并有了初步的了解,教材中也是直接给出相关的定义.但我们不能直接下定义,一读了之.如三角形的定义,它虽然简洁、精确,但却包含着三个层面的意思:一是三条线段组成的图形;二是不在同一直线上的三条线段;三是首尾依次相接.教学时教师应该放手让学生活动,通过摆放肯定与否定的例子,区别概念本质属性与非本质属性.借助大量的实例,引导学生经历概念的概括过程,经历数学语言的不断修改和完善过程,培养学生严密的逻辑思维能力和抽象概括能力.
对锐角三角形、直角三角形和钝角三角形等概念的教学,有的教师认为太简单无需介绍,就让学生自学或直接给出.其实不然,只要仔细思考,就会发现:为什么直角三角形和钝角三角形都是用“有一个角是”,而锐角三角形是用“三个角都是”?这其中蕴涵着逻辑推理和反证法思想.教师要充分挖掘概念中蕴含着的启发学生进行数学思考的元素,从而更好地培养学生的逻辑思维能力.
三、整体把握图形间的联系,提升学生几何直观能力
教材的表述是静态的,知识发展是动态的.几何教学往往需要借助图形的变换,通过图形的变换训练学生思维,培养几何推理和几何直观能力.沪科版教材编写时紧紧抓住基本图形,通过对基本图形的平移、对称、旋转等变换生成丰富多彩的组合图形,其中蕴涵着由特殊到一般的转化思想.
案例3:“全等三角形”一章中,教材安排了如下一些练习.
(1)已知:如图3,点B,E,C,F在同一直线上,AB=DE,AC=DF,BE=CF.求证:AB∥DE,AC∥DF.

图3
(2)已知:如图4,△ABC≌△EBD,那么AC= ______,∠ABE=_______.
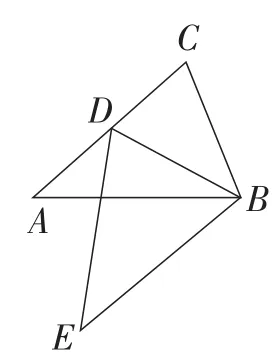
图4
(3)已知:如图5,AB=AC,AD=AE,BD,CE相交于点O,求证:(1)OD=OE;(2)AO平分∠BAC.

图5
这些题目问题不同,图形各异,但它们其实都是由两个全等的三角形分别经过平移、旋转和对称变换
得到,这些图形间的联系和区别蕴含着几何变换的基本规律.
在“三角形中的边角关系”一节中,还有以下例题和练习.
例已知,如图6,△ABC中,BD⊥AC,垂足为点D,∠ABD=54°,∠DBC=18°.求∠A和∠C的度数.

图6
练习:已知,如图7,在△ABC中,AD⊥BC,垂足为点D,∠B=70°,∠BAC=46°.求∠CAD的度数.
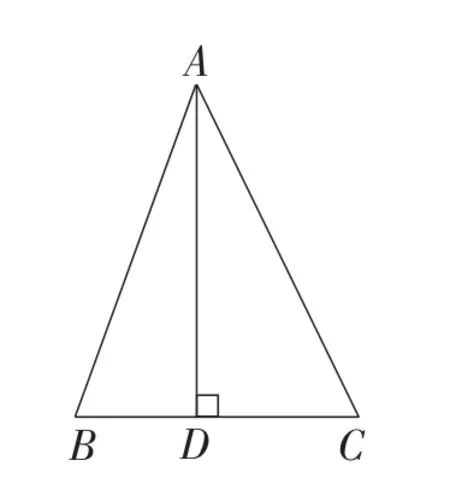
图7
例题是为巩固“三角形内角和是180°”而设定的,既巩固了“三角形内角和是180°”的结论,又通过分析,培养了学生多角度思考问题的习惯,并学会规范书写解题格式.将此题与练习题进行比较,可以发现,只要将例题的图6按顺时针方向旋转90°即可得到练习的图7,通过揭示这两个图形之间的联系和区别,可以培养学生的几何直观能力.
此章中的很多图形都是由基本图形通过变换生成,教学时不能仅限于指导学生解题证明,应该引导学生观察和分析图形间的变换与联系,从而在复杂多变的图形中抓住“不变”的特征.学生对图形的深层领悟是建立在教师深刻理解基础之上的,教师只有深刻理解图形变换间的联系,把握图形变换的基本规律,才能有效指导学生化繁为简,由现象到本质,从而提升几何直观能力.
四、充分挖掘例、习题功能,领悟其中蕴涵的思想和方法
沪科版教材的例、习题都是经过专家反复甄选而配置的,例、习题的教学不仅起着巩固新知、训练技能、形成能力的作用,而且渗透着分析问题的基本方法和思路、解答和表述问题的规范格式,蕴涵着解决问题的数学思想和方法.
案例4:在“三角形中的边角关系”一节中有如下例题和练习.
例等腰三角形中,周长为18 cm.
(1)如果腰长是底边的2倍,求各边长;
(2)如果一边长为4 cm,求另两边长.
练习1:在△ABC中:
(1)已知:∠A=105°,∠B-∠C=15°.则∠C= ______;
(2)已知:∠A∶∠B∶∠C=3∶4∶5.则∠C= ________.
练习2:在一个三角形中,最多只能有一个直角或钝角,为什么?
对于以上问题,有的教师只是简单利用三角形三边关系和“三角形内角和是180°”解决就结束了,没有深入钻研教材,挖掘每一个问题的内涵,这种现象实在令人惋惜.
例题是为巩固三角形三边之间关系而设定,需要用到等腰三角形两腰相等、三角形三边之间关系等知识.通过问题的解决,渗透了用列方程来解决几何问题的方法和分类讨论思想.
练习1既是巩固本节的重点知识“三角形内角和是180°”,也将方程、方程组、比例等有关知识融入其中,使以前所学知识在新的知识体系中得到巩固和应用.
练习2是一个说理题,渗透了反证法思想,对它的分析有助于学生理解为什么锐角三角形定义中必须是“三个角都是锐角”,而直角三角形和钝角三角形只需要“有一个角是直角或钝角”的问题,也为后续学习反证法做铺垫.
教师只有深入研究这些问题,才有可能将它们的作用发挥到极致,达到减轻学生课业负担,提高课堂效率的目的.
《标准》指出,数学教材为学生的数学学习活动提供了学习主题、基本线索和知识结构,是实现数学课程目标、实施数学教学的重要资源.它是教师向学生传授知识、训练技能和渗透思想的材料,是学生成长的“翅膀”.教材的编写,凝聚着很多专家和教师的心血与智慧,只有准确把握《标准》,深入钻研教材,深刻理解教材的编写意图,才有可能用好教材,进而创造性地使用教材.
[1]中华人民共和国教育部制定.义务教育数学课程标准(2011年版)[M].北京:北京师范大学出版社,2012.
[2]马复.初中数学教学策略[M].北京:北京师范大学出版社,2010.
[3]章建跃.中学数学课改的十个论题[J].中学数学教学参考(中旬),2010(1/2):3-6.
2016—07—12
汪洪潮(1968—),男,中学高级教师,主要从事初中数学课堂教学与评价研究.

