全方位扫描中考几何最值问题
李玉荣(江苏省南京市金陵中学河西分校)
全方位扫描中考几何最值问题
李玉荣(江苏省南京市金陵中学河西分校)
通过全方位扫描几何最值问题,给学生提供思考的平台,让学生尝试解决问题的方法,积累基本的解题经验,感悟转化思想,追求解题教学效益的最大化.
中考评价;几何最值;转化思想
《义务教育数学课程标准(2011年版)》指出,评价应以课程目标和课程内容为依据,体现数学课程的基本理念,全面评价学生在知识技能、数学思考、问题解决和情感态度等方面的表现.遵循这一原则,命题者在设计时匠心独具、精心雕琢,在平凡的数学知识考查中制造形式与手段、背景与情境的“奇巧与新意”,作为一个古老而永恒的话题──最值问题,凸显运动变化中的不变思想,体现数形结合、转化与化归的数学思想,更是受到命题者的青睐,其中具有代表性的是“线段”型最值问题,笔者把它们归纳成几种类型,探究解决最值问题的方法,供读者参考.
一、“一动点+一定点”型
例1(2015年湖北·武汉卷)如图1,△ABC,△EFG均是边长为2的等边三角形,点D是边BC,EF的中点,直线AG,FC相交于点M.当△EFG绕点D旋转时,线段BM长的最小值是( ).


图1
解析:点B为定点,点M为动点,
如图2,连接AD,GD,

图2
则∠ADG=90°-∠GDC=∠CDF.
又因为△ADG与△CDF均为等腰三角形,
所以∠GAD=∠FCD.
所以∠GAD+∠DCM=∠FCD+∠DCM=180°.
从而∠AMC+∠ADC=180°.
于是∠AMC=180°-90°=90°.
取AC的中点P,连接BP,MP,
故选D.
【评析】此题有一定的难度,是通过构造三角形,利用“三角形两边之和大于第三边,两边之差小于第三边”,当且仅当三点共线时,第三边取得最小值,这是求“一动点+一定点”型最值问题的一个重要方法.
二、“两动点”型
例2(2015年广东·广州卷)如图3,在四边形ABCD中,∠A=90°,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为_______.
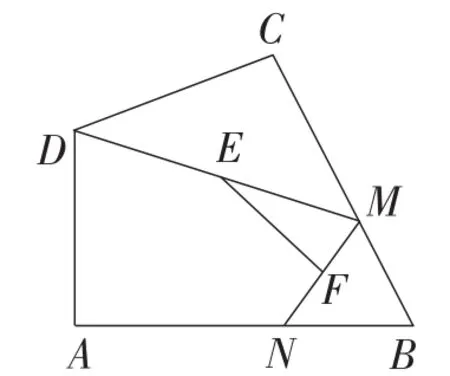
图3

图4
解析:点M,N都是动点,点E,F随之而动,
如图4,连接DN,
因为点E,F分别为DM,MN的中点,
所以当点N与点B重合时DN最大,即EF最大,
故EF长度的最大值为3.
【评析】“两动点”型最值问题,可利用图形条件考虑这条线段与其他线段的关系,一般可通过等量代换转化为“一动点+一定点”型最值,再利用“垂线段最短”求解.
三、“一动点+两定点”型
例3(2015年贵州·安顺卷)如图5,正方形ABCD的边长为4,E为BC上的一点,BE=1,F为AB上的一点,AF=2,P为AC上一个动点,则PF+PE的最小值为______.
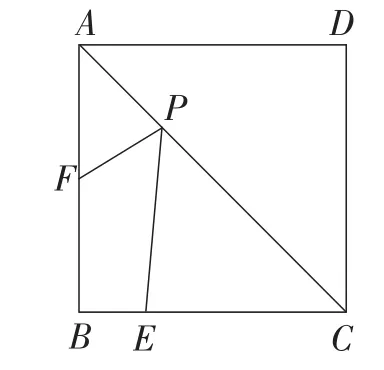
图5
解析:点E,F是定点,点P为动点,且点E,F在AC的同侧,求PF+PE的最小值是常见的一个基本图形问题,一般用对称法求解.
如图6,作点F关于AC的对称点F′,则AF′=AF=2.
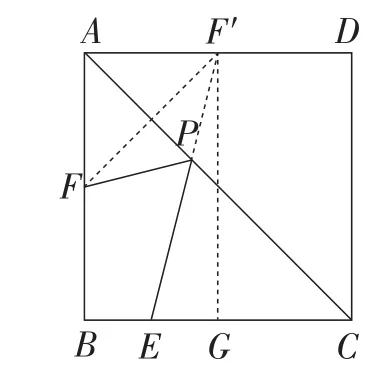
图6
连接F′E交AC于点P,此时PF+PE的值最小,为F′E.
【评析】“一动点+两定点”型最值问题是典型的最值模型,与教材上的一个基本图形密切相关,一般用对称法求解,此类题是各地中考试卷最常考的最值问题.
故PF+PE的最小值为
四、“两动点+一定点”型
例4(2015年湖北·鄂州卷)如图7,∠AOB=30°,点M,N分别是射线OA,OB上的动点,OP平分∠AOB,且OP=6,当△PMN的周长取最小值时,四边形PMON的面积为_______.

图7
解析:点P是定点,而点M,N都是动点,
如图8,分别作点P关于OA,OB的对称点P1,P2,连接P1P2交OA,OB于点M,N,
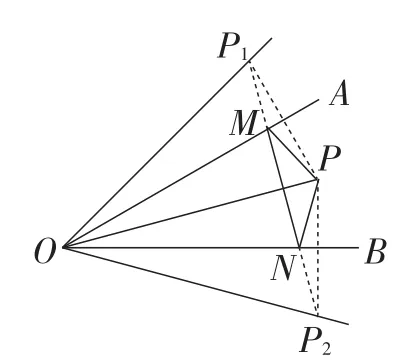
图8
则此时△PMN的周长最小.
连接OP1,OP2,
由∠AOB=30°,知△OP1P2为等边三角形,OP⊥P1P2.
所以P1P2=OP1=OP=6,∠MPO=∠MP1O=60°,∠NPO=∠NP2O=60°,∠MPN=120°.
设P1M=PM=P2N=PN=x,

从而四边形PMON的面积为

【评析】“两动点+一定点”型最值问题难度较大,一般可先将定点关于某条直线的对称点找出来,转化为“三点共线”,或利用“垂线段最短”求解.
五、“两动点+两定点”型
例5(2015年四川·南充卷)已知抛物线y=-x2+ bx+c与x轴交于点A(m-2,0)和B(2m+1,0)(点A在点B的左侧),与y轴相交于点C,顶点为点P,对称轴为l:x=1.
(1)求抛物线解析式.
(2)直线y=kx+2(k≠0)与抛物线相交于两点M(x1,y1),N(x2,y2)(x1<x2),当|x1-x2|最小时,求抛物线与直线的交点M和N的坐标.
(3)首尾顺次连接点O,B,P,C构成多边形的周长为L.若线段OB在x轴上移动,求L取最小值时,点O,B移动后的坐标及L的最小值.
解析:(1)略.
(2)略.
(3)点C,P为定点,点O,B为动点,O(0,0),B(3,0),P(1,4),C(0,3),O,B,P,C构成多边形的周长L=OB+BP+PC+CO.
所以要使L最小,只需BP+CO最短.
如图9,将点C向右平移3个单位得到点C′,
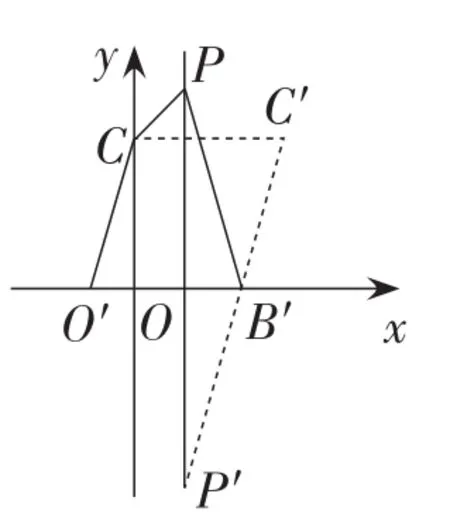
图9
则C′(3,3).
作点P关于x轴对称点P′(1,-4)
连接C′P′与x轴交于点B′,
设C′P′的解析式为y=ax+n,
【评析】“两动点+两定点”型最值问题难度较大,当两动点不在一条直线上时,一般可先作出两定点关于另一条直线的对称点,利用“两点之间,线段最短”求解;而当两个动点在同一条直线上时,需通过平移转化为“一动点+两定点”型问题求解.
六、“三动点”型
例6(2015年江苏·盐城卷)如图10,把△EFP按图示方式放置在菱形ABCD中,使得顶点E,F,P分别在线段AB,AD,AC上,已知EP=FP=4,∠BAD=60°,且
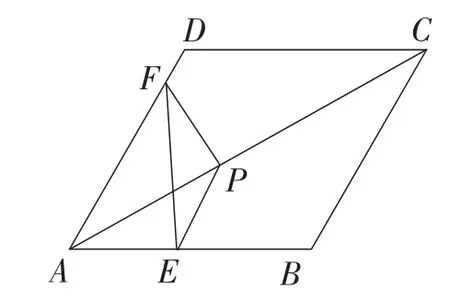
图10
(1)求∠EPF的大小;
(2)若AP=6,求AE+AF的值;
(3)若△EFP的三个顶点E,F,P分别在线段AB,AD,AC上运动,试直接写出AP长的最大值和最小值.
解析:(1)略.
(2)略.
(3)点E,F,P均为动点,
如图11,作PH⊥AB于点H,

图11
则AP=2PH≤2EP=8,当且仅当点H与点E重合时,等号成立.
故AP长的最大值为8.
又因为∠PAB=30°,
所以∠AEP≥∠PEF=∠PAE.
所以AP≥PE=4,当且仅当点F与点A重合时,等号成立.
故AP长的最小值为4.
【评析】此题是“三动点”型最值问题,其最大值是利用“垂线段最短”求解,而最小值是利用“大角对大边”获得.
波利亚说过,数学问题的解决仅仅只是一半,更重要的是解题的反思与回顾.各地中考试卷赋予了几何最值新的活力,精品试题层出不穷,有效地考查了学生分析问题和解决问题的能力.解决此类问题,需要用运动与变化的眼光去研究和观察图形,把握运动中的不变量,针对题目特点,合理地利用“垂线段最短”“两点之间,线段最短”等原理和基本图形,将复杂问题转化为简单的常见问题,当然上述类型中的解法不是孤立的,有时一道题几种方法都能奏效,而有时一道题却需要同时用几个方法才能解决.个中滋味,只有悉心体会,在解题中学习解题,才能实现解题的智慧托举.
[1]李玉荣.点击与圆有关的最值问题[J].中学数学教学,2014(2):63-66.
[2]李玉荣.一组最值问题“圆”来如此容易[J].中学数学(初中版),2015(6):90-91.
2016—08—14
李玉荣(1963—),男,中学高级教师,主要从事数学教学、命题及解题研究.

