中考试题解法“自然性”的四个“引擎”——以2015年江苏省连云港市中考试题第26题为例

孙朝仁（江苏省连云港市教育科学研究所）

中考试题解法“自然性”的四个“引擎”
——以2015年江苏省连云港市中考试题第26题为例

孙朝仁（江苏省连云港市教育科学研究所）

以2015年江苏省连云港市中考试题第26题为载体，呈现生成解题自然性的四个“引擎”，即通过溯源比较引发自然，通过内显变式引向自然，通过原型定向引导自然，通过系统生成引动自然，以此凸显崇尚自然和常规的自然解题要义．

数学试题；解法研究；自然引擎

“自然”取自然而然之意，即按照事物内部规律发展变化．把自然界的这种“自然性”借用到教学领域，则需要教师把握好生成解法自然性的四个“引擎”，即溯源比较、内显变式、原型定向和系统生成．以2015年江苏省连云港市中考试题第26题为例，呈现解题的自然性，以此凸显崇尚自然和常规的自然解题要义．

一、试题解法探析

题目（2015年江苏·连云港卷）在数学兴趣小组活动中，小明进行数学探究活动．将边长为2的正方形ABCD与边长为的正方形AEFG按图1位置放置，AD与AE在同一直线上，AB与AG在同一直线上．

图1

（1）小明发现DG⊥BE，试帮他说明理由．

（2）如图2，小明将正方形ABCD绕点A逆时针旋转，当点B恰好落在线段DG上时，试帮他求出此时BE的长．

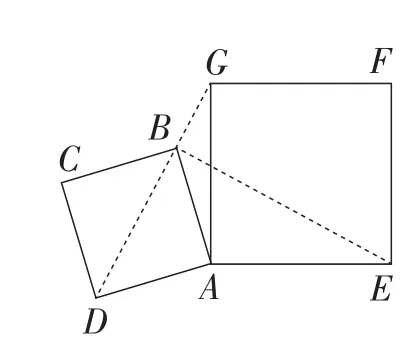
图2

（3）如图3，小明将正方形ABCD绕点A继续逆时针旋转，线段DG与线段BE将相交，交点为H，写出△GHE与△BHD面积之和的最大值，并简要说明理由．

图3

解析：第（1）小题考查了基本图形中两条直线的位置关系，可以借助全等变换获取解答方案.

如图4，延长EB交DG于点M，可得△EBA≌△GDA.

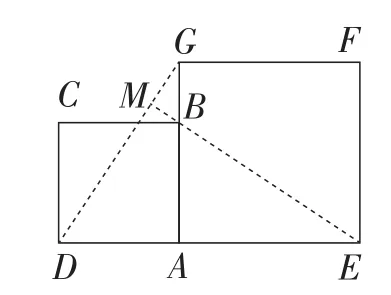
图4

从而得∠MGB=∠AEB.

又∠GBM=∠EBA，进而可知∠GMB=∠EAB=90°.

所以DG⊥BE．

这种基于三角形全等寻求角之间的数量关系，进而获取图形位置关系的方法，是每个学生易想易做的通法，也是解决基本图形问题的自然解法．

第（2）小题考查基本图形的特殊性，可借助操作不变性思想（旋转变换），在全等变换思想指导下获取线段等量关系（DG=BE），将未知线段（BE）转化为可求解线段（DG）．即如图5，过点A作AH⊥DG于点H，利用勾股定理可得从而有这种通过构造直角三角形，获取线段数量关系的方法，在初中阶段是一种普适解法.

图5

而第（3）小题考查了动点问题静态化思想．就△GHE面积最大而言，在底GE为定值的情况下，面积的最大值需要GE边上的高最长．由于无论图形旋转到何位置，总有DG⊥BE，因此，点H是始终在以EG为直径的圆上，显然唯有当点H与点A重合时，△GHE的高最大，此时其面积最大值为4．同时，△BHD的面积也最大，其最大值为2.因此，它们面积之和的最大值为6．这类带有几何直观特征的轨迹类猜想题，学生很容易借助特殊位置关系获取正确答案．尽管有些学生知其然，不知其所以然，但获取正确结果的自然性很大．

二、中考试题解法自然性的四个“引擎”

自然性是指在自然环境中自然变化所引起的自然行为.对于解题教学而言，其解法的自然性需要一定的“引擎”，方能让学生生成解题的自然性.这里的“引擎”主要有通过溯源比较引发自然，通过内显变式引向自然，通过原型定向引导自然，通过系统生成引动自然．

1.溯源比较，引发自然

溯源比较是生成解题自然性的基本引擎，反映解题系统内部的自然属性．这里的“溯源”是对问题来源的追问；“比较”是对同类问题的本质特征的把握．解题要回到自然，回到固有的生动活泼的思考之中．而通过溯源比较可以使得学生尽快进入生动活泼思考的心理状态，可见溯源比较是引发自然解题的起点．

“溯源”就是要寻找教材原型，便于引发自然解题．经过寻找发现，2015年江苏省连云港市中考试题第26题源于苏科版《义务教育教科书·数学》八年级下册第94页习题第16题：点C在线段AB上，分别以AC，BC为边在线段AB的同侧作正方形ACDE和BCFG，连接AF，BD．（1）AF与BD是否相等？证明你的结论．（2）如果点C在线段AB的延长线上，（1）中所得的结论是否成立？试画出图形并证明.

此中考试题改变了设问的方向，由探索数量关系转移到对位置关系的探寻，并对数量关系进行深度探究，包括对线段长度的求解和对面积最值的思考．

“比较”就是要思考解决同类问题的本质特征，为解题教学提供理性思维的自燃性．经比较，笔者联想到2014年江苏省连云港市中考试题第27题的前两道小题，试题如下.

某数学兴趣小组对线段上的动点问题进行探究，已知AB=8．

问题思考：如图6，点P为线段AB上的一个动点，分别以AP，BP为边在同侧作正方形APDC与正方形BPEF．

图6

（1）当点P运动时，这两个正方形的面积之和是定值吗？若是，试求出；若不是，求出这两个正方形面积之和的最小值．

（2）分别连接AD，DF，AF，AF交DP于点K.当点P运动时，在△APK，△ADK，△DFK中，是否存在两个面积始终相等的三角形？试说明理由．

苏科版《义务教育教科书·数学》八年级上册第68页习题第5题就研究了“母子型”图形的相关问题，只不过设问方向与2014年江苏省连云港市中考试题第27题考查角度不同：教材习题是从面积和周长的角度直接预设的，而2014年江苏省连云港市中考试题第27题“问题思考”是从函数和等积选择的角度设问的.在这样的比较中，自然获得一类试题的常规解法．在教学中，如果教师能经常引导学生思考问题的来源，并比较同类问题的本质特征，那么学生见到陌生问题就能自然寻求到问题解决的突破口，提高解题效率.

2.内显变式，引向自然

内显变式是生成解题自然性的关键引擎．变式是排除概念非本质属性干扰的重要手段，内显变式是解题自然性形成的关键策略．而由变式到解题行为发生的本身，又是实现解题思维跃迁的自然过程.其间，内显变式（变化参数设置、变换试题背景等）是引向解题自然的主要动力来源，当然并不排除外显变式（数量关系的变化、图形位置的变化等）的助推作用．无论是外显的还是内显的都反映解题教学需突破同一背景的变式思想．

心理学家马斯洛指出，学习者具有发自内心的生长力，教师的重要任务在于设置良好的学习环境，让学生自行学习．这里的“生长力”“学习环境”“自行学习”可理解为形而上的自然性因素，前者应该与原始自然属性对应；后两者应该与生产自然属性吻合．因为只有基于自然的背景中，方能让学习者的思维有序，向平稳过渡，实现解题自然．

从教材原型到2015年江苏省连云港市中考试题第26题的变式来说，显然属于内显变式．前者考查了静态直观和动态变化融合的较为直接的数量关系，而后者考查了基于位置变化背景背后的数量关系．就试题

示例内部逻辑关系来说，第（1）小题属于显性变式，利用几何直观可自然解决；第（2）小题属于隐性变式，需要进行构造与化归相结合来解决；第（3）小题属于外显变式，需要思考并抓住运动变化中的不变量，进而思考运动状态下的“极端”情形（最大值）．三道小题由浅入深，层层递进，又相互关联，在变式中让学生学会数学的思维，形成解题的自然属性.

3.原型定向，引导自然

原型定向是生成解题自然性的重要引擎．自然解题的过程就是学习者定向原型的自然而然过程．这里的“自然”就是顺应学生的心理发展水平，“而然”就是让问题思维水平尽可能与不同学习者的知觉水平自然衔接．这就要求试题本身具有清晰的原型起点，方能让学习者的解题思维逻辑连贯、模型清晰．就教材习题原型的思维起点而言，就是基本图形数量关系的建立（AF与BD是否相等），而初中阶段借助全等变换是获得线段数量关系的自然通法，因此原型定向具有选择心理水平层面的自然性．2015年江苏省连云港市中考试题第26题的思维起点，就是基本图形位置关系的建立（小明发现DG⊥BE，试帮他说明理由），而初中阶段借助概念是获得特殊位置关系的常规路径，这就为构造直角三角形埋下思维的自然伏笔．无论是教材原型还是试题示例，最终都是通过全等变换实现自然的解答．因此，全等变换是试题组块的自然通法，同时，定量分析自然解法的过程，又促进了原型定向的自然反哺功能．

依据心理学家安德森的心智技能形成三段论（认知阶段、联结阶段和自动化阶段），笔者认为，心智技能形成的逻辑起点就是原型定向与现有思维水平的一致性．真正的自然解法应该是原型定向的自然化序列过程，由教材原型到试题示例中采用的全等变换，其思维水平是梯级递进的自然过程．前者是直接变换的结果（全等三角形对应边相等的性质），后者是间接变换的结果（借助全等三角形对应角相等的性质，利用三角形内角和定理，获得直角的等量关系）．试题示例三个设问间的内部关系，均是以“垂直”这一位置关系为自然思维的起点，第（2）小题借助勾股定理解决问题，第（3）小题借助圆周角定理得以解决．而定理是高级思维的自然形态，时时监控学生的思维走向，有利于简单化思考，引导生成解题的自然性．

4.系统生成，引动自然

系统生成是引动解题自然性的高级引擎．“系统”在这里可理解为解题对象、解题矛体和解题受体，以及由受体转化为矛体的过程性因素的组合．“生成”具有不稳定性和不平衡性，可理解为在个体思维最近发展区的原型内化形态性和层次性，体现人人都能获得良好数学教育的课程理念．

系统生成引动解题自然主要体现在以下三个层面：一是学生自然想到的通性、通法；二是易于操作的常规性方法；三是具有清晰的思维线索，可水平关联和垂直联结．试题示例的三个设问可抽象成“图形位置关系—线段数量关系—面积数量关系”．从水平关联特征来看，揭示“数量—位置—数量”之间自然水平转换关系．这就要求解题时，关注位置关系中的自然解法（全等变换），只要在位置关系视野下，后续的自然思维将迎刃而解．从垂直联结特征来看，反映“化归—操作不变性—几何直观—数形结合”之间的相互补位．这就要求解题教学时，应用力于把握逻辑分析、逻辑监控和逻辑呈现，以及反例补偿等行为要素，方能引动自然解题，体现试题自然解法的功能．

任何科学都关心某种变化中不变的东西，而哲学关心普遍的规律．这里“不变的东西”不是“能指”而是“所指”，在解题领域可解释为系统生成的物质化外壳，具有独特性和不均衡性．换句话说，也就是不同个体在解题自然的反哺下，可获得不同层面的发展．而“普遍的规律”则是自然的自然属性，具有理性审美意识，在解题领域具有“常规”“通性”之美．也可以理解为，自然解法是尚简的、大道的和审美的．

生成自然解法，除了需要有自然的载体（中考试题）来承载，还需要用自然的引擎来引领，更需要拥有自然意识的主体（学习者）来显化．因此，解法自然不止于对具体问题的通法、通性的研究，而在于对解题教学系统各要素自然属性的表征研究，体现系统解题自然观．

［1］张逢臣，王志进.探索解题方法自然生成的轨迹［J］.中学数学教学参考（中旬），2015（4）：29-31．

［2］尤维明.探寻解题方法自然生成的源泉［J］.中学数学教学参考（中旬），2015（6）：49-50．

［3］云鹏，李健.得之自然成之天然［J］.中学数学教学参考（中旬），2015（6）：50-51．

［4］［德］菲利克斯·克莱因.高观点下的初等数学［M］.舒湘芹，陈义章，杨钦樑，译.上海：复旦大学出版社，1989．

2016—08—01

孙朝仁（1967—），男，正高级中学高级教师，主要从事初中数学教育与教学研究及科研管理.