对一道中考压轴题的解法探究

顾建锋（浙江省嘉兴市南湖区教育研究培训中心）

对一道中考压轴题的解法探究

顾建锋（浙江省嘉兴市南湖区教育研究培训中心）

经过对2015年浙江省嘉兴市中考试题压轴题最后一道小题的深入探究，突破了解答此题的思维难点.从不同的思维角度来思考此题，得到了不同的解题切入口，从而用多种方法解答了此题，同时对各种解法进行了简要回顾．

解法探究；数学关系；解法回顾

一、试题呈现

题目（2015年浙江·嘉兴卷）类比等腰三角形的定义，我们定义：有一组邻边相等的凸四边形叫做“等邻边四边形”．

（1）概念理解.

如图1，在四边形ABCD中，添加一个条件使得四边形ABCD是“等邻边四边形”．写出你添加的一个条件．

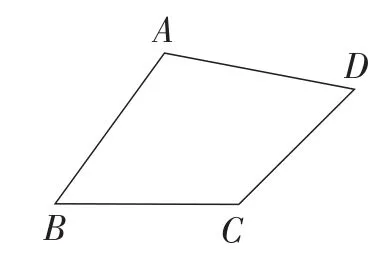
图1

（2）问题探究.

①小红猜想：对角线互相平分的“等邻边四边形”是菱形．她的猜想正确吗？试说明理由．

②如图2，小红画了一个Rt△ABC，其中∠ABC= 90°，AB=2，BC=1，并将Rt△ABC沿∠ABC的平分线BB′方向平移得到△A′B′C′，连接AA′，BC′．小红要使平移后的四边形ABC′A′是“等邻边四边形”，应平移多少距离（即线段BB′的长）？

图2

（3）应用拓展.

如图3，“等邻边四边形”ABCD中，AB=AD，∠BAD+∠BCD=90°，AC，BD为对角线，试探究BC，CD，BD的数量关系．

图3

此题是2015年浙江省嘉兴市中考试题的压轴题．试题以新定义为背景，题干文字精炼，图形外观简洁，设问递进探究，尤其是第（3）小题虽条件清晰，但需要添加辅助线才能解题，对学生的思维能力要求很高，笔者在阅卷过程中发现能够完整解答出第（3）小题的学生寥寥无几．阅卷结束后笔者进行了仔细研究，现把第（3）小题的解题思路整理出来与大家分享，以期得到各位同行的指正．

二、解法探究

在探究此题多种求解思路时，笔者发现该题蕴含了丰富的数学内容，解法多样.

1．在特殊位置寻找数量关系

解答第（3）小题最大的难处在于待求结论不明确，找不到未知量、已知量、条件之间的直接联系，于是思考，能不能使条件、结论都特殊化？在这样的思维驱动下之下，笔者进行了如下思考.

（1）如图4为对角互余的等邻边四边形的作图方法：①作Rt△AED，使∠ADE=90°；②在斜边AE上截取线段AB=AD，连接BD；③作△BDE的外接圆，并在该外接圆上任取一点C，则四边形ABCD即为对角互余的等邻边四边形，并且这样的等邻边四边形可以作出无数多个．

图4

（3）由条件∠BAD+∠BCD=90°，考虑将∠BAD和

图5

2．从条件入手探索证题方法

（1）以旋转变换知识为切入口.

面对题设条件“AB=AD”，从静态角度看能想到等腰三角形；从动态角度看，想到旋转变换，利用旋转将分散的角度、线段聚集．这是常见的思路．

解法1：如图6，将△ADC绕点A旋转到△ABF处，连接CF，

图6

则△ADC≌△ABF.

所以∠ADC=∠ABF，∠DAC=∠BAF，AC=AF，CD=FB.

从而得到△ACF∽△ABD.

又因为∠BAD+∠ADC+∠BCD+∠ABC=360°，

所以∠ABC+∠ADC=360°-(∠BAD+∠BCD)=360°-90°=270°，

得∠CBF=90°，

结论得证．

（2）以直角三角形知识为切入口.

面对题设条件“∠BAD+∠BCD=90°”，勾股定理浮现眼前，于是自然联想到构造直角三角形，这是解题的起点，接着思考将已知的两角怎样合并成一个直角，依据图形特征，在顶点C或点A处尝试构造直角，可以将零散的已知条件集中，为后续问题的探究铺平道路．

解法2：（方法1）如图7，过点C作∠DCG=∠BAD，截取CG=CD，连接DG，BG．

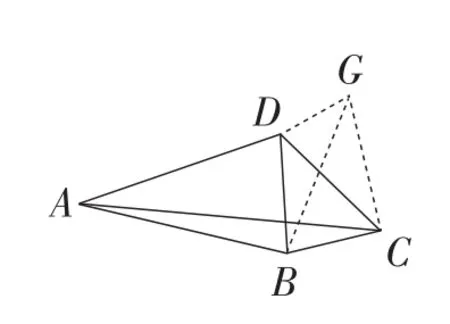
图7

因为∠BAD＋∠BCD＝90°，

所以∠BCG=90°.

由勾股定理，得BC2+CG2=BG2，

即BC2+CD2=BG2．

因为△ADB∽△CDG，

于是∠ADC=∠BDG.

所以△ADC∽△BDG.

（方法2）如图8，过点A作∠3=∠1，∠4=∠2，分别交CB，CD的延长线于点E，F，连接EF．

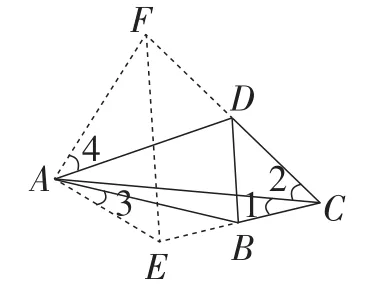
图8

由此容易推出∠EAF=90°和△EAB∽△ECA.

所以AE2+AF2=EF2，且

进而推出BC=BE．

再由上述条件不难推出EF=2BD.

即BC2+CD2=2BD2．

（3）以相似三角形知识为切入口.

解法3：如图9，分别延长AB，AD至点E和点F，使DF=AD，BE=AB，连接CF，CE，EF，

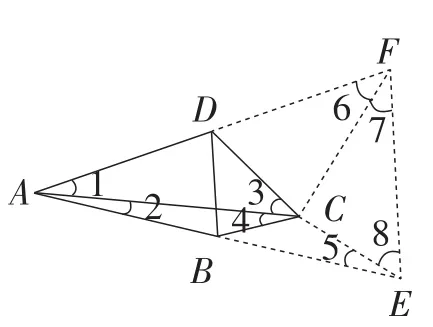
图9

则BD是△AEF的中位线，

从而得到EF=2BD.

于是△ABC∽△ACE.

得∠4=∠5，

又因为∠1+∠2+∠3+∠4=90°，

所以∠1+∠2+∠5+∠6=90°.

所以∠7+∠8=90°.

由勾股定理可得CE2+CF2=EF2.

即BC2+CD2=2BD2．

3．由结论变形引领证题方向

结论“BC2+CD2=2BD2”与勾股定理的符号表述相接近，引领证题的方向指向直角三角形，但结论“BC2+CD2=2BD2”毕竟有别于勾股定理的符号表述，于是考虑将结论“BC2+CD2=2BD2”变形为或从而突破思维瓶颈，将问题转化为直角三角形的构造或证明．

解法4：（方法1）如图10，过点B作BF⊥BC，使得BF=CD，连接AF，CF．

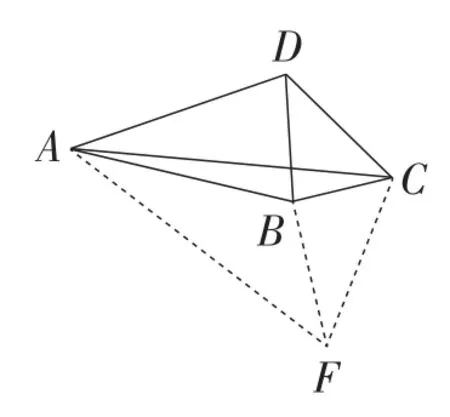
图10

易得∠ABF=∠ADC.

从而可证得△ADC≌△ABF.

（方法2）如图11，在对角线AC上取一点E，使∠ABE=∠1，连接DE．

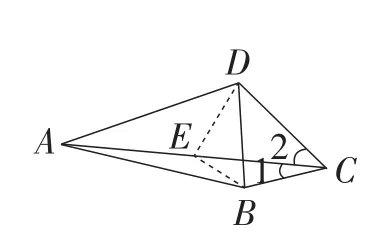
图11

易得∠BEC=∠BAC+∠1，且△ABE∽△ACB.

所以△ADE∽△ACD.

再由∠BAC+∠DAC+∠1+∠2=90°，得∠DEB=90°.

所以BE2+DE2=BD2，

即BC2+CD2=2BD2．

三、解法回顾

题目第（3）小题的解答从特殊图形探究数量关系开始，到一般图形下数量关系的探究结束，历经特殊到一般，以及先猜想后证明的思考过程．其中一般图形下数量关系的探究，解法多样，既异中有同，又各有千秋．

以旋转变换知识为切入口，解法巧妙，过程简洁，学生容易理解，但在平时的学习中，旋转变换的应用背景一般出现在特殊三角形（等腰三角形和等边三角形）和特殊四边形中（菱形和正方形），此题是在条件相对弱化的特殊四边形中，而且还是一个陌生四边形——等邻边四边形，学生不容易想到.所以，这种解法的思维起点是对旋转变换应用背景的一种补充，解答的关键是在图形中提炼出基本图形，即等腰三角形，进而想到运用旋转变换构筑辅助线．

以直角三角形知识为思维起点，学生虽容易想到，却难于入手．解题时根据对角互余的条件或结论“BC2+CD2=2BD2”的特征，构造合适的直角三角形是问题解答的首要条件，其次是运用相似三角形的知识找到边之间的关系结合勾股定理方能解决问题．

以相似三角形的知识为思维起点，学生的思维可能会多次受阻．解答时借助已知条件先构造相似三角形，再利用对应边、对应角之间的关系，以及勾股定理解决问题，虽属常规思路，但需添加辅助线众多，步骤繁杂，对学生的思维能力是一种挑战．

［1］范宏业．2014年安徽省中考第23题的解法分析［J］．中国数学教育（初中版），2015（5）：16-19，64.

2016—07—18

顾建锋（1975—），男，中学高级教师，主要从事中学数学教学与命题研究.