“三角函数线”在《三角函数》教学中的研究现状及教学建议
江苏省扬州市新华中学 (225009)
赵久勇 孟素红
“三角函数线”在《三角函数》教学中的研究现状及教学建议
江苏省扬州市新华中学 (225009)
赵久勇 孟素红
“三角函数线” 是三角函数概念中的一个辅助概念, 是用几何中的有向线段数值表示三角函数值的一种数形结合方法.现行高中教材《必修4(苏教版)》第12至13页中给出了正弦线、余弦线、正切线的定义,其目的是使我们在研究三角函数及解决三角问题时, 既可利用坐标系中代数工具的运算之便, 又可借助单位圆内几何图形的性质之利.但教材限于篇幅原因, 对于本可贯穿整个三角学习的三角函数线, 仅在描绘三角函数的图像、探究三角函数的性质时, 作了部分的应用,给人颇有利器初露锋芒即告收敛之感,笔者对近年来有关期刊刊登的有关“三角函数线”文章进行梳理,现将研究现状概括如下:
1 “三角函数线”在三角函数学习中的应用综述
1.1 解释三角函数定义
设α是一个任意角,它的终边与单位圆交于点P(x,y),则OM=x,MP=y与cosα=x,sinα=y相对照.用单位圆上三角函数线来解释三角函数,可以使正弦函数、余弦函数从自变量(角的弧度数)到函数值(单位圆上点的横、纵坐标)之间的对应关系更清楚、简明,突出了三角函数的本质,也使三角函数反映的数形关系更直接明了,为后续的研究奠定基础.
1.2 方便记忆三角函数在各个象限内的符号
由三角函数线的作法和三角函数的定义可知,某一个三角函数在同一个象限内的符号是一样的.如正弦的符号取决于P点纵坐标y的符号,余弦的符号取决于横坐标x的符号,若P点在第二象限,x<0,y>0.事实上,当P点在第二象限时,正弦线MP方向向上,数量为正,余弦线OM方向向左,数量为负,因此第二象限内的正弦为正,余弦为负;同样可得正切为负的,其余象限内的三角函数的符号也可一一确定.
1.3 明晰三角函数的定义域
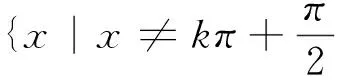
1.4 加深对三角函数性质的理解
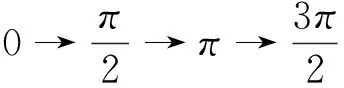
即随着角α值的增大,余弦值相应减小,从而余弦函数在[0,π]上是单调递减的.正弦函数、正切函数单调性类推可得.
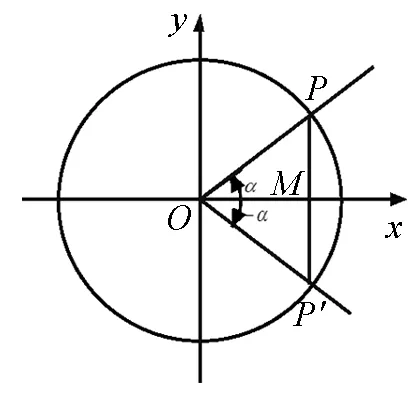
图1
(3) 奇偶性:如sinα,不论α如何,-α的终边OP′与α的终边OP关于x轴对称(如图1),这时,它们的正弦线长短相等,方向相反.即MP′=-MP⟺sin(-α)=-sinα.同理,余弦函数、正切函数奇偶性类推可知.
1.5 辨别同角三角函数的基本关系
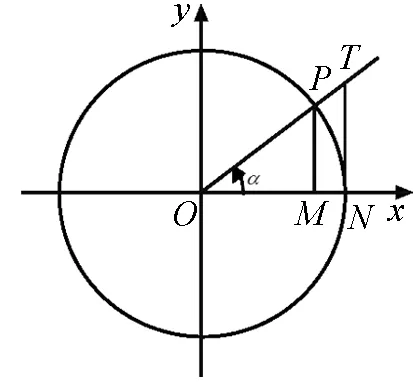
图2
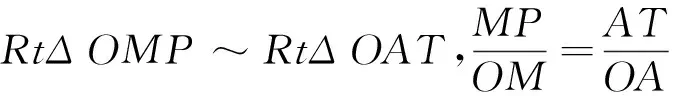
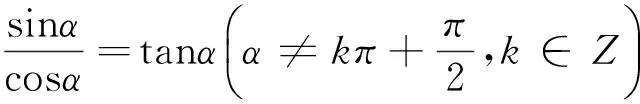
1.6 推导三角函数的诱导公式
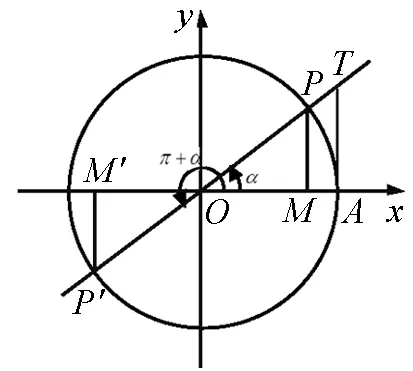
图3
由于单位圆具有很好的对称性,因此可以通过对单位圆上对称点对应的角的三角函数线来推导诱导公式.下面以诱导公式(二):f(π+α)=±f(α)为例来进行探究(如图3).
设角α的终边OP与单位圆的交点为P,则P点关于原点O的对称点P′也在单位圆上,终边OP′对应的角是π+α,观察角α和π+α的各三角函数线,正弦线分别是MP和MP′,余弦线分别是OM和OM′,正切线都是AT,且MP=-MP′,OM=-OM′,即有sin(π+α)=-sinα,cos(π+α)=-cosα,tan(π+α)=tanα.
2 “三角函数线”在解决数学问题中的应用
2.1 求三角函数的值
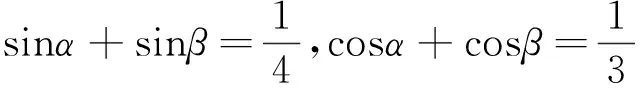
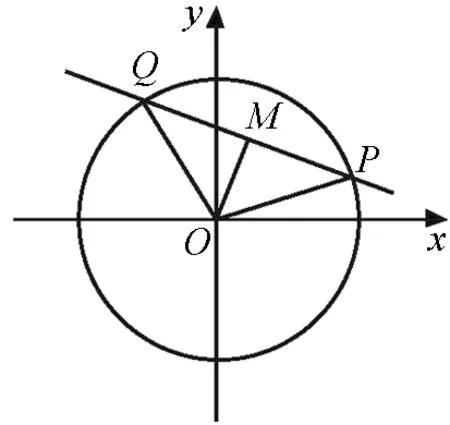
图4
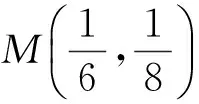
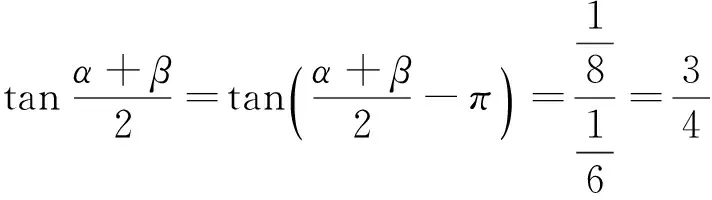
2.2 比较三角函数值的大小
例2 设α∈[0,2π) ,试比较sinα与cosα的大小关系
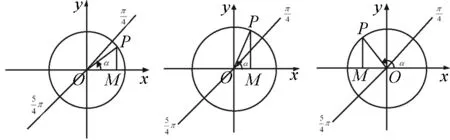
图5-1 图5-2 图5-3
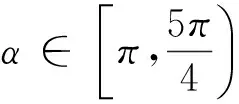
|OM|(如图5-4),MP>OM,即sinα>cosα;
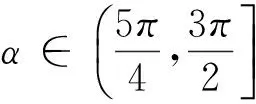
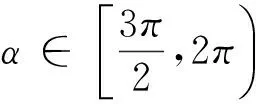

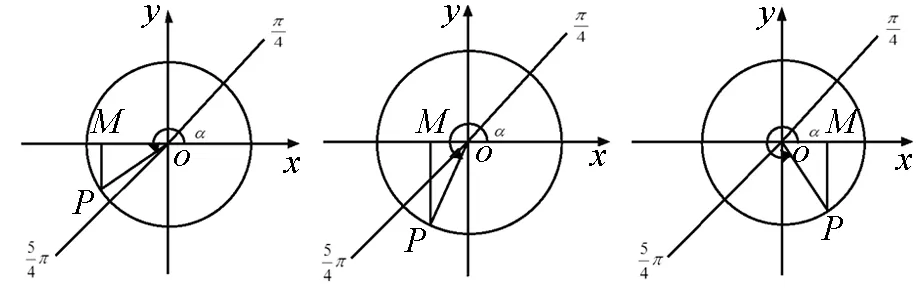
图5-4 图5-5 图5-6

2.3 解三角不等式
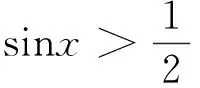
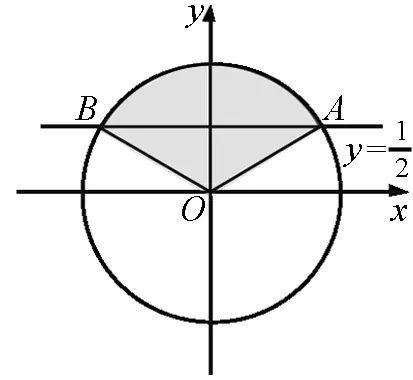
图6
2.4 证明三角等式和不等式
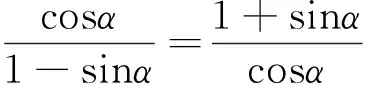
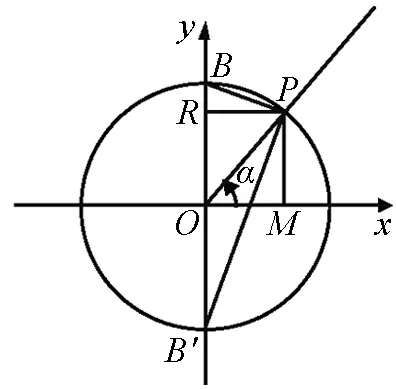
图7
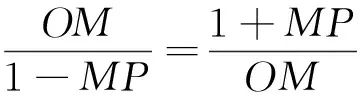
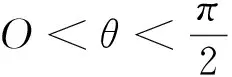
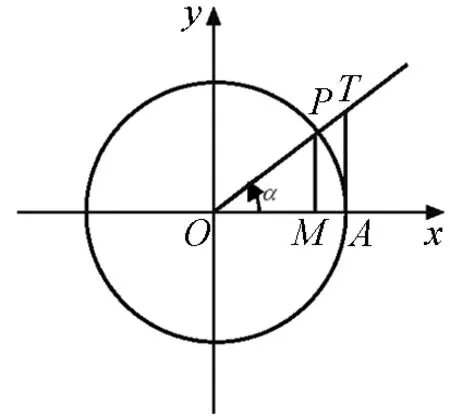
图8
3 教学建议
纵观以上研究,“三角函数线”的教学对学生的解题有很大帮助.但为使学生对于“三角函数线”定义的理解及生成过程不再疑惑重重, 为使学生在透彻理解定义的基础之上,更加清晰的应用其解题.
笔者认为教师在教学时需注意以下几个问题:
问题1 为什么用单位圆,其他圆是否可以?
问题2 为什么过点A(1,0)作单位圆的切线?过其他点是否可以?

图9
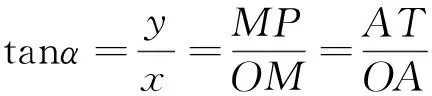
问题3 为什么当α为第二、三象限角时切线交其反向延长线于点T?
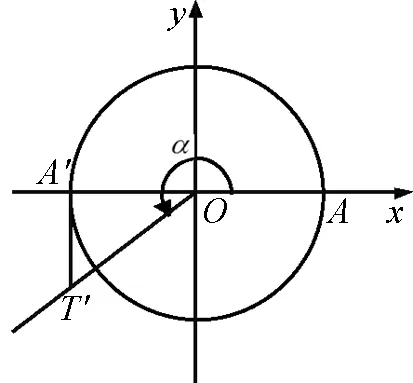
图10
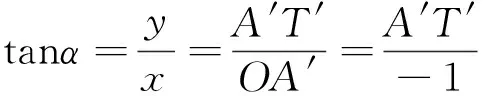
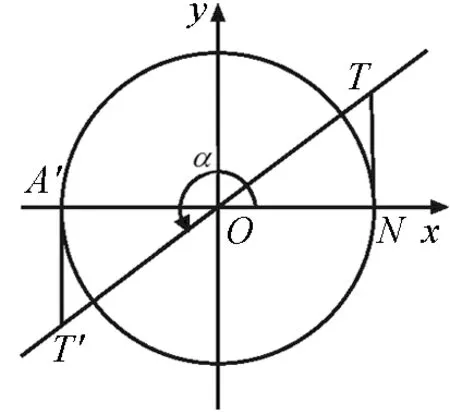
图11
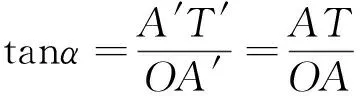
4 教学尝试
当然,在本届高一教学中,为了更好的便于学生对“三角函数线”的理解及应用,我尝试将教材中所介绍的“三角函数线”作了适当的修改(保留其使用几何图形来理解三角的思想).操作如下:
定理 sinα=α的终边与单位圆交点的纵坐标;cosα=α的终边与单位圆交点的横坐标; tanα=α的终边(或反向延长线)与单位圆正切线(过A与单位圆相切的直线)交点的纵坐标.
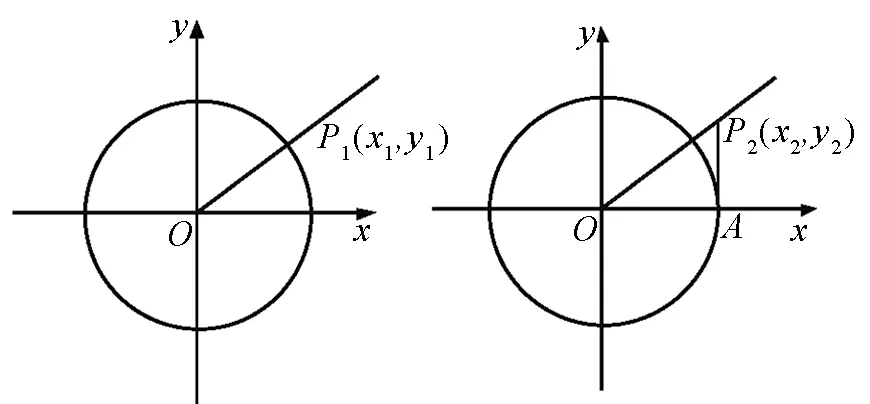
图12 图13
证明:(如图12)作单位圆,设角α终边与单位圆交点为P1(x1,y1).因为r=1,由正、余弦函数定义知sinα=y1,cosα=x1;(如图13)设角α终边与单位圆正切线交点为P2(1,y2),由正切函数定义知tanα=y2.
上述定理具有以下两大优点:
一.定理推导简便,推导过程中只用学生刚学过的三角函数定义,学生容易理解和掌握,同时对巩固三角函数定义也起到了积极作用.不需再引入“有向线段” 的有关概念,产生过程自然易懂,学生很容易接受.
二.定理完全能够很好的保留“三角函数线”的几何作用,而且应用范围更广.由于定理是将三角函数值与相关点的一个坐标直接对应,使用起来非常方便.除了作三角函数图像以外,还可轻松解决判断三角函数值的正负、比较三角函数的大小、已知三角函数值求角、解三角不等式等.
[1]陈曦,张海玲,王尚志.HPM 视角下“任意角三角函数的概念”教学研究[J].首都师范大学学报( 自然科学版),2014,12(第35卷第6期):23-27.
[2]王学先.三角函数中有趣的“楚河汉界”———“三角函数线”数学拓展型新课教学过程简录及评析[J].中国数学教育,2012,6:28-32.
[3]田新.三角函数线[J].数学通讯,1996,11:1-3.

