MPCK视角下的核心概念教学——观摩“向量的概念及其表示”课的体会与思考

浙江省宁波市北仑明港高级中学 (315806)

李鑫娟



MPCK视角下的核心概念教学
——观摩“向量的概念及其表示”课的体会与思考

浙江省宁波市北仑明港高级中学 (315806)

李鑫娟

数学教学内容知识(Mathematic Pedagogical Content knowledge ,简称MPCK)MPCK是关于某一特点的数学教学内容该如何进行表达、呈现和解释，从而使学生更容易接受和理解的知识.按照香港中文大学黄毅英教授的观点，MPCK是三个基本集：MK、PK、CK的公共部分.其中，数学学科知识(Mathematics Knowledge 简称MK)；一般教学法知识(Pedagogical Knowledge 简称PK) ；有关数学学习的知识(Content Knowledge,简称CK， 包括教学对象——学生学习背景、学习环境、教学宗旨等方面的知识)三者地位相当，MPCK即上述三者的交集.

数学知识几乎都是概念，而对学生今后生活起到观念性影响的是数学中的一些核心概念、核心思想方法.核心概念、核心思想方法的抽象性、层次性、表征多元性决定学生对它的理解需要经历一个不断往复、逐步加深、螺旋上升的过程.我们在教学中似乎忽视了几个核心问题：数学是什么？课堂是什么？学生是什么？宁波市李惠利中学特级教师苏茂鸣老师亲自开设研讨课《向量的概念及其表示》，这节课使人耳目一新，以其独到的见解和处理方式向我们展示了如何对数学的核心概念进行有效教学，如何在核心概念的教学中追逐数学的本质，如何让学生在核心概念的教学中习得数学的核心思想，又如何让数学课堂浸润数学文化.整节课也始终追求：自然的数学、自由的课堂、自主的学生，一气呵成，自然连贯.笔者听课后，感触颇深，回味无穷，粗浅提笔谈谈对此节课的体会与思考.

一堂有效的数学课应该有一条主线把教师与学生的理解、倾听、认知形成一条线索，促进双方的理解和感悟.教师可以更好的驾驭课堂，学生可以更容易的建构本节课的新内容融入现有的知识体系，更好地达成教学目标.苏老师遵循“直通始终、明确方向、整体连续”的注意点，理出了“问题情景——提出问题——学生活动——意义建构——数学理论——数学应用——反思提升”这样一条主线，教学效果证明，这是一条行之有效的核心主线.

(一)生活感知 初识概念

引子 章节引言

设计意图：向量概念不是凭空产生的.用一个简单直观的问题让学生感受“既有大小又有方向的量”的客观存在，自然引出学习内容，使学生更有亲切感，有助于激发学习兴趣.从而使学生体会向量是沟通几何性质和代数运算的高速公路，没有运算，向量只是一个“坐标”，因为有了运算，向量的力量才无限，使他们真正感受到向量引入的必要性.

问题1 一艘船从港口O出发，向东航行了3千米到达A处，又航行了60千米到达B处，遇到意外情况需要派直升机援助.请问：直升机应该到何处寻找该船？

学生发现：(1)该船没有告知速度(2)该船没有告知航行方向，无法确定船只的位置.

设计意图：通过实例创设情境，源于学生的最近发展区，使学生初步感知即将学习的概念的实际背景，明白学习的必要，产生求知欲.

(二) 感知积累 内化概念

问题2 你能举出哪些既有大小又有方向的量？哪些只有大小，没有方向的量？

学生举例：既有大小又有方向的量:位移、速度、力、加速度；只有大小没有方向的量：时间、距离、长度.

在学生举例的同时，苏老师巧妙地就着学生的话语引出了数学史的内容，以伟人牛顿的光辉人格魅力感染学生，对他们进行了一次心灵的洗涤.恰到好处地穿插数学史，不仅丰富了课堂内涵，更让我们看到了苏老师的博学和对课堂的把握.

设计意图：形成区别不同量的必要性，概念抽象需要丰富典型的实例，让学生举例可以观察到他们对概念属性的领悟，形成对概念的初步认识.学生的直观感知经验十分重要，但切不可超之过急，否则感知就会成为过场，当感知多次重复形成“共同的印象”，下一步就可以进行联想和想象，从而对感知的内容进行内化，为形成概念作铺垫.

(三)抽象概括 同化概念

定义1 我们把既有大小又有方向的量叫做向量；把只有大小没有方向的量叫做数量.

定义2 带有方向的线段叫作有向线段，数学上用有向线段表示向量.

设计意图：在经历了直观感知和想象内化后，苏老师和学生们一起通过“去粗取精，去伪存真，由此及彼，由表及里”的反复提炼推敲，利用学生认知结构中原有的有关概念来同化向量这一核心概念，抽象概括出向量的本质特征，这样的设计显得顺其自然，同时也为概念的应用埋下伏笔.

类比实数的构成，在实数中的数字“0”和“1”，在对数的学习和后继的运算都有着举足轻重的地位.那么向量中有那些特殊的向量呢？

定义4 单位向量：长度等于1个单位的向量.

设计意图：向量的引入是为了简化计算，优化数学解题方法，特殊向量的引入是为了完善向量的体系，没有运算的向量就没有生命力.

(四)实际应用 活化概念

例1 (完善问题1)一艘船从港口出发，以20km/h的速度向东航行3小时到达A处，又向南航行了60km到达B处.

(1)画出该船的两次位移；

(2)画出从O到B的向量，并说说该向量的大小和方向.

例2 下列说法正确的是( ).

A.平面直角坐标系xoy中的x轴是向量

B.单位向量一定大于零向量

D.有向线段就是向量，向量就是有向线段

概念活化是指数学概念从其无活性状态变为具有活性的过程，通常表现为灵活运用概念解决实际问题，目的是进一步深刻理解概念，培养迁移能力.

设计意图：向量本身就具备代数和几何双重属性，问题1的引入本身就具有开放性，以问题为驱动，同时可以为后继概念的学习引用.给出概念并不意味着概念就在学生的脑袋里生根发芽了，这只是概念形成的开始，从而例题2是在定义给出后对概念进行的辨析，即适当做一些“逗留”从正反两方面辨析向量是什么，什么不是向量，如何用文字和符号表征向量概念，以加深学生对概念的理解.

(五)辨析理解 固化概念

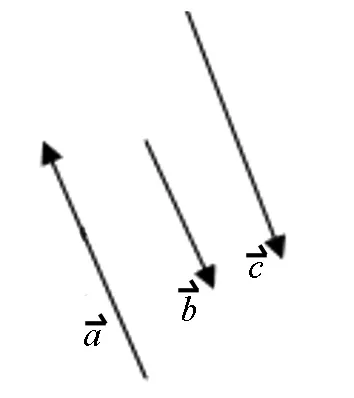
图1

定义5 相等向量：长度相等且方向相同的向量.

规定：零向量和零向量是相等向量.

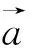
设计意图：学生活动可以有效调动学生的兴趣和积极性，让他们从大小和方向两个方面展开思考，教师适时介入，强化本质特征，规范概念表达，与学生一同完成概念的定义.

相等向量和平行向量是对向量的再次审视，从特殊的位置进行深度的挖掘，对概念的形成过程进行回味，思考概念定义语句的含义和特点，揭示概念的内涵和外延，把握相关概念的区别和联系，从而达到对概念固化的目的.教师多媒体课件的演示更让学生直观感知，形象记忆，同时也给学生学习向量的流程的回味，加深对向量本质的理解，如何对新知识点展开自主学习.

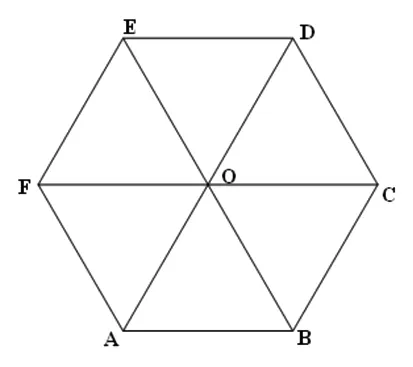
图2

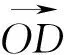
练习：下列说法正确的个数为( ).

A.0 B.1 C.2 D.3

设计意图：通过例题活用，巩固概念.在问题的解决中，把握相关概念的区别和联系，引导他们经历从具体实例中领悟向量概念的本质，类比数的概念获得向量的概念，类比数的集合认识向量的集合，类比直线的基本关系认识向量的基本关系.在题目中体会认识一个数学概念的基本思路，而不是死记硬背一个概念.

(六)反思过程 顺化概念

(1)本节课我们研究了一个新的数学概念——向量，主要研究了哪些内容？

(2)从今天概念产生的过程和问题解决的过程看，对你以后的学习有什么启示？

(3)本节课老师送你们几句话：方向长度两要素，类比实数有特殊；三次规定零向量，相等共线(平行)慎看图.

(4)课后体验：(象棋中的跳“马”问题)在象棋棋盘中，“马”每走一步就确定一个向量(位移).起初“马”在点A处，最终目标是“马”要到达点B处.为实现这个目标①请你设计一种走法，并在图中画出向量表示；②在你设计的走法中，是否可以出现共线但不相等的向量？举例说明.

设计意图：这样设计帮助学生顺化概念，理解整个向量的概念体系，从而达到有点连线的整体感，为学生完全掌握概念，形成有序的认知结构提供帮助，同时概念的产生和问题的解决过程也为后继的学习提供借鉴平台.课后归纳和体验更是把这节课提升了一个高度.

从MK的角度看，本节课的例子和例题都是苏老师在MPCK的三个维度，比较和吸取教材及现实生活中的典型实例，体现了数学学科的特点：抽象性、逻辑性、结构性，全面反映了数学教与学的特点.以发展智力、培养能力和创新能力为出发点，具有典型性和代表性.向量是本节课的核心概念，因为它是沟通代数、三角和几何的桥梁，对更新和完善数学知识结构起着重要的作用.它不仅有着丰富的实际背景和几何背景，作为数学模型，它广泛地应用于解决数学、物理学科和实际生活中的问题，在整个高中数学中的地位是不言而喻的.本课不仅要理解向量概念、更要了解概念产生和发展的过程，渗透基本的数学思想方法.在教学活动中始终贯穿：从具体实例和章头图引入向量的概念及几个特殊向量；从大小和方向两方面刻画向量的本质，让学生体会认识研究数学新对象的方法和基本思路，从而提高提出问题分析问题和解决问题的能力.

从PK的角度看，在概念的引入部分，首先是从日常生活或数学中有代表性的事例入手，分化出相关概念的属性，从而概括出其共同属性.并在特定的情境中检验，确定关键属性.本节将数学思想和数学史有机的结合，发挥了“数学育人”的功能.引言使学生从一个比较宏观的角度了解即将学习的新内容——向量的特点和意义，感受数学文化的魅力，同时起到“先行组织者”的作用，激发了学生有意义学习的心向，提高了学习的效率.在概念形成的过程中，均采用“归纳——表征——精致——内化”的过程，体现人类的认知规律，在初步表征概念时渗透类比的思想，并在概念的内涵和外延的锤炼中，精致和内化数学概念，优化学生的数学认知结构.

从CK的角度看，不同认知水平的学生对该问题的认识有一定的差异，特别是在引入阶段如何做到“开启全章、奠定基调、渗透方法”，要求体现新课程理念的教材，提出了大量具有思考价值的问题，让学生带着问题学习，尽可能展示知识的发生、发展过程.在宏观上苏老师为学生勾勒出研究框架和整体思路，学生能“抬头看”，知道往哪里走，这也是起始课的重要任务；微观上，引导学生通过类比，有序地给出向量的定义、讨论向量的表示、定义特殊向量、研究向量的关系，这样的编排是符合学生的认知规律的.在课堂教学流程的设计上，重现知识的发生和发展过程.在教学预设和课堂动态生成取得平衡的过程中，让流畅的教学过程成为学生经历概念的产生和发展以及问题的解决过程，也成为学生在教师的指导下进行意义建构概念、实现“再创造”的过程.

概念教学是高中数学教学的一个难点，教师要在自身的MPC多下功夫，站在人的发展和课程相融的高度，把精力集中在数学核心知识及其思想方法的学习和研究上，不断提高自己.路漫漫而修远兮，吾将上下而求索！