对2016年四川卷高考理科10题的研究

四川省内江师范学院数学与信息科学学院 (641100)

余小芬 刘成龙



对2016年四川卷高考理科10题的研究

四川省内江师范学院数学与信息科学学院 (641100)

余小芬 刘成龙

2016年是四川省高考自主命题的最后一年，2017年将回归全国统一命题．基于此背景，2016年四川卷的总体特点是：“稳定不乏新颖，平和不掩亮点”．整张试卷在平稳过渡的同时，涌现了一大批优秀试题，比如：理科第5题、6题、10题、15题、18题、19题、21题等等．这些优秀试题不仅具有良好的测评功能，而且是研究的良好素材．本文仅对理科10题进行研究，权作抛砖引玉！

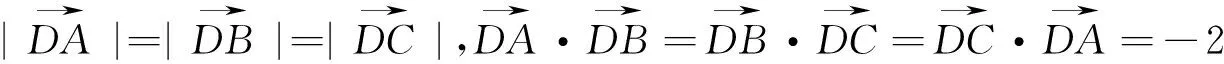
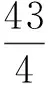
该题是四川卷选择题中的压轴题，具有构思巧妙、背景公平、形式新颖、内涵丰富等特点，是四川卷中的亮点题．下文从试题立意、试题背景、试题解法、试题推广、试题改编五个视角对该题进行研究．

1.试题立意

试题立意是指试题的考查目的．命题者基于考查目的，选择适当的考查内容、拟定恰当的考查形式、设置合理的数学问题．把握试题的立意不仅是透过题目表层意义把握试题本质的过程，更是再现命题者思维智慧的过程．下面从考查基础知识、考查思想方法、考查能力素质三个方面分析该题的立意．

第一、以考查基础知识立意．本题以平面向量的基本概念、线性运算、数量积、垂心、外心的向量表示以及点的运动轨迹等基础知识为考查内容．

第二、以考查思想方法立意．本题考查了数形结合、化归与转化等数学思想方法．解答本题，首先需要把题目中信息转化为对应的几何图形，再把最大值问题转化为熟悉的三点共线问题或向量共线或三角问题或条件最值问题．

第三、以考查能力素质立意．本题考查了考生思维能力、运算能力、推理能力．解答本题需要经历两个环节：

第一环节 首先需要通过推理得到D为外心和垂心，进而得到ΔABC是等边三角形，这是解答试题的难点；其次根据题意画出几何图形，这是解答试题的关键点；最后通过运算得到ΔABC的边长．

第二环节 根据图形拟定恰当的方法是解答的重点．试题求最值的解答思路很多，比如向量法，三角函数法，柯西不等式法等，但数学思维能力较强的学生，直接基于三点共线可轻松解答，真正做到“多想少算”．

2.试题背景

试题背景指命题时试题取材的背景．试题背景引领试题编拟的方向，凸显试题的立意．研究试题背景，可以准确把握试题的本质、认识试题的情景、理解试题的设问、拓宽试题的解法、加强试题的拓展．常见的试题背景有教材背景、现实背景、高考数学背景、高等数学背景、竞赛数学背景、数学史背景等等．下面重点分析该题的教材背景．

教材背景1 源于教材习题

源于人教版《高中数学》必修4第二章《平面向量》复习参考题B组第5题、第8题(120页)：

教材背景2 源于教材例题

源于人教版《高中数学》必修2第四章《圆的方程》例5(122页)：

例5 已知线段AB的端点B的坐标是(4,3)，端点A在圆(x+1)2+y=4上运动，求线段AB的中点M的轨迹方程．

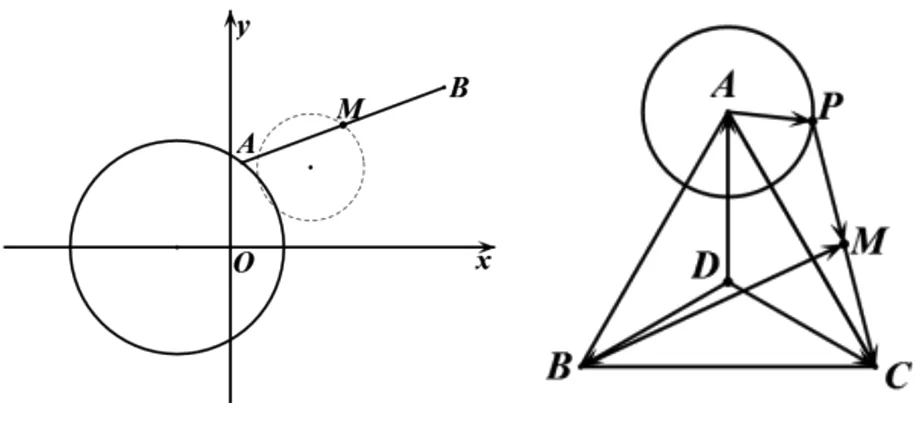
图1 图2

3.试题解法

试题的解法研究是研究高考试题的主要形式和重要内容．解法研究的主要方法有一题多解、多题一解等等．其中，一题多解指从不同视角对同一问题进行分析进而得到多种解答方法．通过对解法间共性与差异的把握，既能让学生认识问题的本质，又能培养学生的发散思维．

解法研究的首要环节是理解题目(波利亚语)．具体来讲，解题者应该搞清楚“未知量是什么？已知数据是什么？已知条件是什么？已知条件能推出哪些结论.”

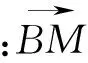
题设条件推出的信息：

(1)⟹①D为ΔABC外心；

(3)⟹P在以为A圆心, 半径为1的圆周上.

(4)⟹M为CP的中点．

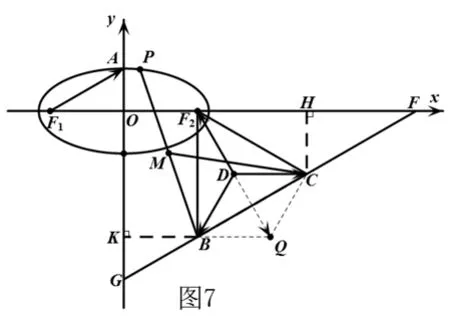
对以上信息进行加工处理，可以得到与题意相匹配的几何图形(图2)，下面从不同的视角给出该题的多种解答．

视角1 平面几何的视角

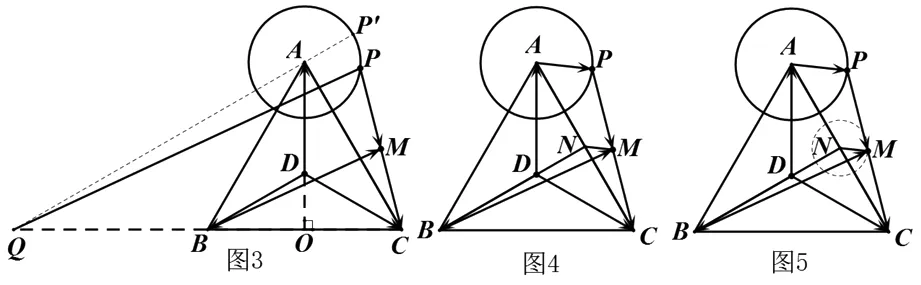
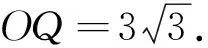
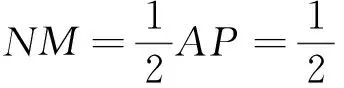
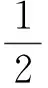
视角2 向量的视角

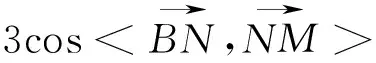
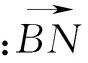
视角3 解析法的视角

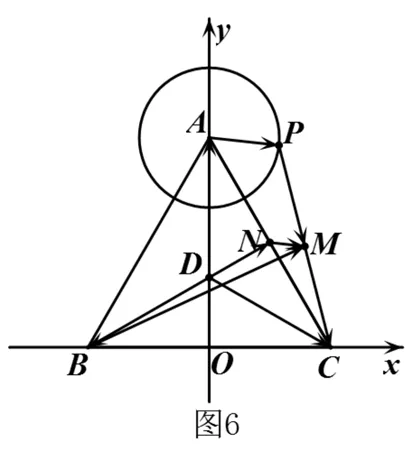
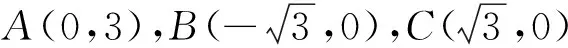
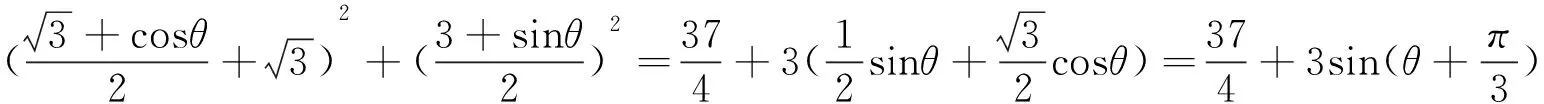
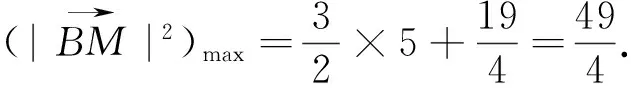
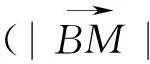
4.试题推广

试题推广是指通过变式把已有试题变成更一般的试题．试题推广有利于完善学生认知结构．试题推广的方法有：增加元的个数、提升元的次数，数字字母化，结论一般化等等．

试题推广 在平面内，定点A,B,C,D满足

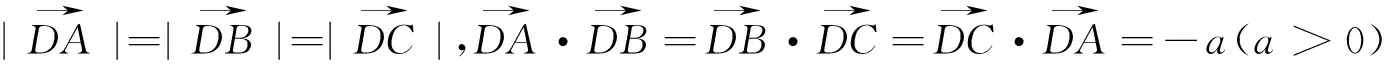
点评：把10题中的数字字母化，得到了比10题更一般的结论．

5.试题改编

试题改编是研究高考试题的重要方式．试题改编有利于深化对问题的本质认识，有利于实现解法的迁移．试题改编的基本方式有：变换试题背景、强化或弱化已知条件、改变设问方式等等．

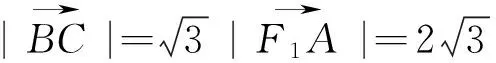
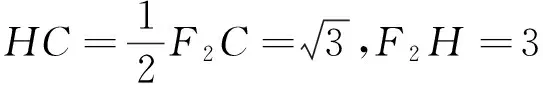
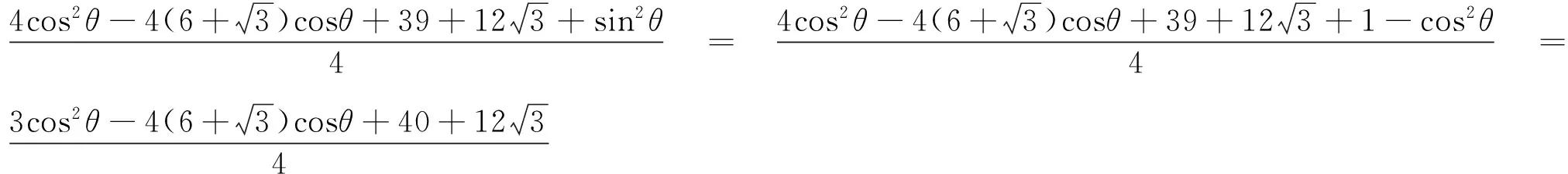
令cosθ=t(t∈[-1,1])，故

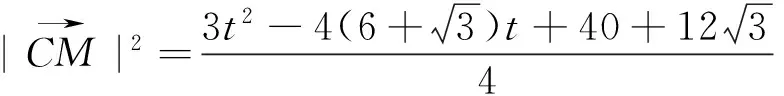
至此，笔者从5个角度对四川卷理科第10题进行了深入研究，希望有兴趣的老师们继续前行！

[1]赵思林．高考数学解题分析[M]．四川：四川大学出版社2011．

[2]刘成龙，余小芬．研究高考试题的几点方法[J]．中学数学研究(江西)，2008,9．