从学生解题难点看解法自然生成

浙江省温州市第十九中学 (325000)

何 萍 张 莎



从学生解题难点看解法自然生成

浙江省温州市第十九中学 (325000)

何 萍 张 莎

1.试题

2.解法展示

图1

图2

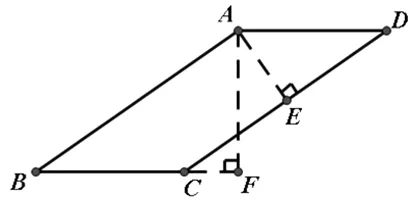
图3

3.解题思考

3.1 解法错误难点分析

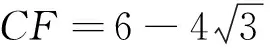
3.2 难点解决的自然生成策略

基于以上难点分析，设计解题认知活动，展开解题过程教学.

问题1 一个周长是28的平行四边形是确定的吗？

启发学生画出不同形状的平行四边形(图4)，体会一个周长是28的平行四边形是不确定的，四条边和四个内角都是变量.

由问题1的启发，学生画出图1和图2.

追问：你是怎么作出这两个图形？

启发学生根据条件求得AD=6，AB=8后，再由这两条高线在平行四边形内或外的位置不同产生分类.

追问：当平行四边形的边或角中，哪些量变化时，会产生了这两条高线不同的位置？

启发学生进一步认识当平行四边形内角变化或边长变化时，引起ΔABC和ΔACD的形状变化，出现钝角三角形、直角三角形、锐角三角形，导致这两条高线位置在四边形内或外部.

问题3 你能求出哪些线段的长？

学生求出线段DE、CE、BF、CF的长.

追问：观察以上线段是否都符合实际情况？

引导学生发现在图(1)下，CF的值不符合实际情况.即当CF的值为负数时，说明BF>BC.

问题4 你怎么调整平行四边形的形状，使得BF>BC？

引导学生在图1的基础上将图形调整到图3求解.

本题解答对分类讨论的获得不是一蹴而就的，而是经历去伪存真的发现和循序渐进的突破后逐步形成的.这种历经挫折后的调整与变通，并且自然而然想到的解题方法，渗透分类思想，才是切合学生需要的自然解法.

3.3 解法自然生成的思考

所谓自然解法，不应当是针对某一问题的某一种特定的解法，自然解法应当是基于解题者的知识结构和思维习惯而产生的一种最本能的反应，最容易想到的方法，是解题者的一种原生态的思考方式.现在的解题教学中，教师往往用自己已有的经验方法去强化学生练习，而忽略了学生解题中的思维难点.长此以往，容易造成学生解题的思维定势，导致碰到没见过的题目就无法入手.笔者认为，数学解题核心目标是发展数学认知和元认知水平，解题教学的切入点应该从引导学生自然合理的数学思考入手，通过设计合理的解题认知活动，让学生独立自主地发现解题思路，在解题的认知活动中发展数学认知水平和元认知水平，提高分析问题和解决问题的能力.尤其重视针对学生解题难点启发思考.对于解题者在解题心理过程中，出现的解题思路受阻、解题方向错误、解题方法不当等难点，基于尊重学生原生态的思考方式，从培养学生思维品质的角度，帮助学生突破难点，教会学生思考.