初中数学运用反例法教学探讨

福建省尤溪县管前中学 郑忠

初中数学运用反例法教学探讨

福建省尤溪县管前中学 郑忠

反例法和反证法同属于数学逆向思维的两个不同的层面.反证法的教学只限于认识即可，因为深入的反证法在高中阶段才是重点.反例法教学对学生数学思维的发展意义重大，是培养学生的逆向思维，将来进一步学习反证法的必经之路.

初中数学 反例教学 逆向思维

初中数学新课标中关于在反例和反证法的教学中，要求学生能够“通过具体的例子理解反例的作用，知道利用反例可以证明一个命题是错误的”；“通过实例，体会反证法的含义”.下面结合教学实践，就初中数学教学中，运用反例法教学谈一些看法和做法，以期抛砖引玉.

一、反例的作用

反例不仅在培养逆向思维能力中占重要地位，同时在纠正错误结论、澄清概念、开拓数学等新领域中也起到了非常重要的作用.我们可以说（撇开定义、陈述及艰苦的工作不谈）数学由两大类，即证明和反例组成，而数学的发现也是朝着这两个主要目标，即提出证明和构造反例.由此可见反例之重要.

二、反例教学的具体操作

在新课程标准实施中，我们更加重视反例教学.学生能创造性的构造反例，对培养学生思维的逆向性、缜密性、克服思维定势、优化思维品质具有无可替代的作用.

1.培养缜密的逆向思维.

在讲授三角形全等的识别方法时，学生从正面探讨“边角边（SA S）”、“角边角（A SA）”、“边边边（SSS）”时比较容易理解，但要理解为什么“边边角”不成立时感觉比较困难.

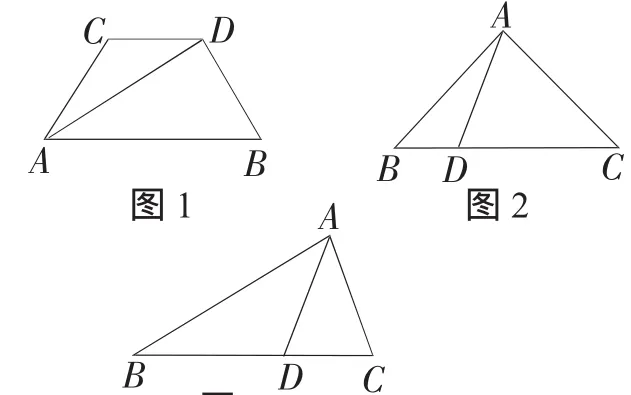
图3

此时提示学生研究反例，笔者在教学中发现和总结出了如下几个反例供同行们参考：

（1）如图1，四边形ABDC是等腰梯形，△ACD和△ABD满足两边对应相等（AC=BD、AD=AD）及其中一对应边的对角相等（∠CDA=∠BAD），但显然△ACD和△ABD不是全等.

（2）如图2，等腰△ABC中，AB=AC，D是BC上一点，△ACD和△ABD满足两边对应相等（AC=AB、AD=AD）及其中一对应边的对角相等（∠B=∠C），但显然△ACD和△ABD不是全等.

（3）如图3，在△ABC中，AC=AD，则△ABD和△ABC满足两边对应相等（AC= AD、AB=AB）及其中一对对应边的对角相等（∠B=∠B），但显然△ABD和△ABC不全等.

2.克服思维定式，优化思维品质.

例如，我们知道：在圆中，等弦所对的圆心角相等，则下述命题“等弦所对的圆周角相等”吗？反例如图4，弦AB所对的圆周角∠C≠∠D，所以这个命题是假命题.

图4

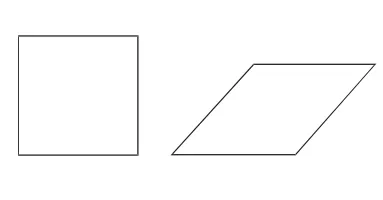
图5

又如，如果两个三角形的三边对应成比例，那么两三角形相似，那么对于两多边形，学生也容易认为，“对应边成比例的两多边形相似”.我们举一个反例就可以使学生印象深刻地认识到自己的错误：一个正方形和一个菱形（图5），显然它们的对应边成比例，但它们不相似.同样地，对应角相等的两多边形相似吗？我们可以举一个长方形和一个正方形（图6）作为反例，它们的对应角相等，但它们并不相似.

再如，命题“在圆中，如果直径平分弦，则必垂直弦”是否正确？学生可能受到垂径定理的干扰，或者自己随手画了画，就认为这个命题是对的.其实我们很容易忽视图7的这个情形.

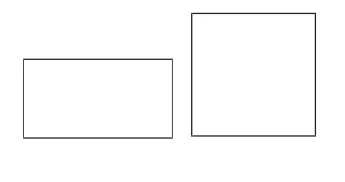
图6

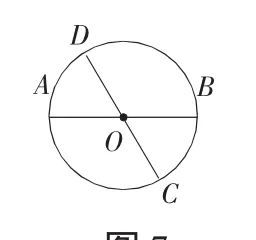
图7

3.挖掘思维深度，培养创造能力.

例：判断命题“一组对边及一组对角相等的四边形是平行四边形”是否正确，说明理由.

反例构造1：如图8，四边形ABCE是平行四边形，通过A、C、E三点画圆O，以点A为圆心，AE为半径画弧交圆O于点D，连接AD、CD.则∠E=∠D，AE=AD；又因为∠B=∠E，所以∠B=∠D；且AE=BC，所以AD=BC.所以在四边形ABCD中，有AD=BC，∠B=∠D，满足命题的条件，但显然四边形ABCD不是平行四边形.

图8

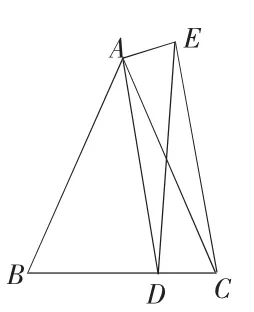
图9

反例构造2：如图9，△ABC是等腰三角形，AB=AC，在边BC上取一点D，连接AD，作∠ADE=∠DAC，截取DE=AC.则△ADC≌△DAE，所以DE=AC，且∠ACD=∠AED.所以四边形ABDE满足一组对边相等（AB=DE），一组对角相等（∠AED=∠B），但显然四边形ABDE不是平行四边形.

反例构造3：其实是上例的更简洁易懂的说法：如图9，等腰△ABC中，D是BC上的一点，现用剪刀将△ADC沿着AD剪下，翻转后如图△AED位置粘上，则四边形ABDE就是满足要求的反例.