特征选择的多准则融合差分遗传算法及其应用

关晓颖， 陈果，林桐

南京航空航天大学 民航学院， 南京 210016

特征选择的多准则融合差分遗传算法及其应用

关晓颖， 陈果*，林桐

南京航空航天大学 民航学院， 南京 210016

为了全面评价特征子集的好坏，提高特征子集作为最佳子集的可靠性，以及更快找到最佳子集，提出了一种用于特征选择的多准则融合差分遗传算法。引入多个评价准则对特征子集进行评价，并对遗传算法的选择算子进行改进，有利于选出适应度高且具有重要特征的个体；同时，引入差分策略改进变异算子,提高种群多样性和算法搜索能力；最后通过仿真实验和滚动轴承实例验证了该方法的有效性。

特征选择； 多准则； 差分进化； 遗传算法； 滚动轴承； 故障诊断

特征选择的任务就是求出一组对分类最有效的特征，即在特征维数减少到同等水平时，其分类性能最佳。Filter法和Wrapper法是常用的方法。Filter法利用单独的可分性准则来选择特征；Wrapper法利用分类器进行特征选择[1]。由于Wrapper法是直接利用分类器的错误率作为特征选择的依据，具有特征选择精度高的优点，但由于每次选择子集后都需要进行学习训练，耗时大。而Filter法的单个评价准则不能全面评价特征子集的好坏。基于此，特征选择既要定义有效的可分性准则进行特征评价，还需要设计有效的算法提高最优特征组合的可靠性和搜索效率。

特征选择的过程可以看作是一个求解组合优化问题的过程，因此可以用解决组合优化问题的方法来解决特征选择问题。遗传算法(Genetic Algorithm，GA)在这方面具有很大的潜力，尤其当选择的空间很大(特征维数很高)且对特征间的关系缺乏认识时。遗传算法通过模拟自然界中生物进化的遗传规律寻找最优的进化结果，属于带导向性的随机优化算法，具有良好的全局搜索能力和隐含的并行性。目前，遗传算法被广泛应用于特征选取，国内外学者对基于遗传算法的特征选择方法进行了研究并取得良好的效果[2-8]。

然而，现有应用于特征选择的遗传算法中，对于Filter方法，更多是采用单个评价准则；其次，在GA的改进上，未充分考虑特征权重对GA搜索的引导性，以及传统的变异算子不容易变异得到更多的优秀个体。有鉴于此，本文提出一种用于特征选择的多准则融合的差分遗传(Differential Evolution and Genetic Algorithm with Multi-criteria Evaluation, MEDEGA)算法，算法的第1阶段采用ReliefF算法[9]获得特征权值，为第2阶段的GA搜索提供先验知识和导向；第2阶段提出差分遗传算法，以简单遗传算法(Simple Genetic Algorithm, SGA)为基础，利用特征权值，并结合适应值对选择算子进行改进，以及采用差分策略改进变异算子，另外，还以特征子集作为整体进行评价；第3阶段注重最优特征子集的可靠性评价，在每次GA终止时得到的结果进一步评价，选择频繁出现的特征或特征组合，避免偶尔出现的特征所产生的干扰。算法实现了加快种群收敛速度，提高算法性能，有效改善特征选择的效果。最后，用仿真实例验证了方法的有效性，并将方法应用于滚动轴承故障特征的选择研究，得到了滚动轴承故障诊断的最优特征子集。

1 多准则融合差分遗传算法

1.1 算法基本流程

遗传算法是模拟遗传继承和达尔文的适者生存原理，它以适应度函数(或目标函数)为依据，通过对群体施加遗传算子操作来实现群体内个体基因重组的迭代处理过程，逐代演化产生出越来越好的近似解。遗传算法的实现涉及5个主要因素：个体的编码、初始群体的设定、适应度函数(评价函数)的设计、遗传算子(选择、交叉、变异、精英策略)和算法控制参数。特征选择的过程就是一个求解组合优化问题的过程，为了求得最优特征子集及提高算法的性能，遗传算法要重点解决的问题有：① 构造适应度函数；② 遗传算子(选择、杂交和变异)的设计。

针对Filter方法的单个评价准则不能全面评价特征子集的好坏，为了提高选择精度，以及提高特征子集作为最佳子集的可靠性，本文提出了多准则融合差分遗传算法用于特征选择，分别从3个方面去选择和评价特征子集：第一，单个特征对分类的贡献，为GA搜索提供先验知识和导向。采用ReliefF算法计算单个特征权值，权值越大，则该特征对分类的影响就越大；第二，特征子集作为一个整体进行评价，选取类间距离大、类内距离小的特征子集；第三，提高最优特征子集的可靠性，避免偶尔出现的特征所产生的干扰，结合多次测试的结果，选择频繁出现的特征或特征组合。图1为基于多准则融合的特征选择示意图，图2为MEDEGA算法的流程图。

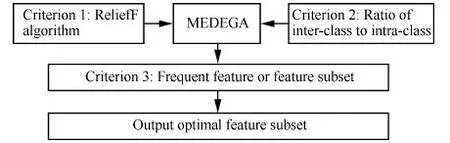
图1 基于多准则融合的特征选择示意图Fig.1 Illustration of feature selection based on multi-criteria

图2 提出的多准则融合差分遗传(MEDEGA)算法流程图Fig.2 Flowchart of proposed differential evolution and genetic algorithm with multicriteria evaluation (MEDEGA) algorithm

1.2 算法关键技术

1.2.1 ReliefF算法

ReliefF算法[9]是Kononenko在1994年提出的，它是一种改进的Relief算法，也是目前Filter特征选择的方法之一，它主要用于处理多类问题以及回归问题。通过不断调整权值，使得和类别相关性高的特征赋予较高的权值。

算法的主要思想是：每次从训练样本集D中随机取出一个样本Ri，找出与样本Ri同类的k个最近邻Hj，对每个类C≠class(Ri)，找出与Ri不同类的k个最近邻Mj(C)，然后根据式(1)更新每个特征的权值：

(1)

式中：diff(A,R1,R2)表示样本R1和样本R2在特征A上的差；m为重复次数。diff(A,R1,R2)的计算公式为

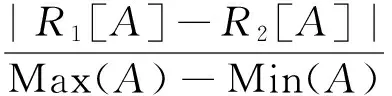
(2)

然而，虽然ReliefF算法适合处理具有大量实例的高维数据集，评估效率高，在噪声过滤方面表现优异，但它不能去除冗余特征[10]。

1.2.2 适应度函数

由于特征之间可能存在不同程度的相关性，不应只关注单个特征对分类的贡献，应将特征子集作为一个整体进行评价，选取类间距离大、类内距离小的特征子集。因此，本文定义特征子集的类间距离与类内距离之比作为适应度函数，其计算公式为

(3)

式(3)中的分子衡量了类间的疏散程度，值越大，则说明类间越疏散；分母衡量了类内的聚集程度，值越小，则说明类内越聚集。

1.2.3 特征权值与适应值相结合的选择算子

采用ReliefF计算得到特征权值，得到了单个特征对分类的贡献；适应度函数从类间与类内距离计算特征子集整体对分类的贡献。特征权值作为先验知识，为算法搜索提供导向性，将适应度高且具有重要特征的个体选出，本文设计了特征权值与适应值相结合的选择算子，具体如下：

1) 计算特征子集权值的均值；假设特征子集的特征个数为n，W(Ai)为特征Ai的权值，则计算特征子集权值的均值为

(4)

2) 计算个体k的适应值在种群中的比重

(5)

式中：m为种群规模；fk为个体k的适应值。

3) 计算个体被选择的概率

pk=t·aver+(1-t)Sk

(6)

式中：t为[0,1]的随机数，表示适应值与特征权值的比重。本文取t=0.5。

4) 计算累积概率以构造一个轮盘。

5) 轮盘赌选择：在[0,1]区间内产生一个随机数，若该随机数小于或等于个体k的累积概率且大于个体k-1的累积概率，则选中个体k。

1.2.4 差分变异

差分进化(Differential Evolution，DE)是一种基于群体差异的启发式随机搜索算法，变异操作方面使用差分策略，即利用种群中个体间的差分向量对个体进行扰动，实现个体变异。DE的变异方式有效利用群体分布特性，提高算法搜索能力，避免遗传算法中变异方式的不足[11]。

本文采用了改进的差分变异[12]，在每一个新个体的生成过程中用到了父代多个个体的线性组合, 而不是遗传算法传统单一的父代染色体交叉技术；并且根据两个父体的度量距离来决定变异基因位数，然后根据式(10)计算基因值。有利于提高种群的多样性和提高算法的搜索能力。具体如下：

1) 随机选择3个不同父代个体r1、r2、r3。

2) 计算两个父代个体的距离

(7)

3) 确定个体变异基因数，p为(0,1)随机数。

(8)

4) 每个基因位的变异：随机选择一个基因位i，设该基因位的值表示为hi；根据选出的3个父代个体，使用式(9)计算它们在基因位i的线性组合并赋给hi,即

(9)

式中：F为缩放因子，一般是取值范围为 [0,2]的常量，用于控制差分向量的扰动程度。经验表明F取值太小容易使种群过早收敛，而F取值过大时算法收敛速度会明显下降[13]。本文取F=1.0。

由于r1,r2,r3的取值是0或1(文中所有GA的编码方式均采用二进制编码)，这3个变量取值就有8种组合，而根据式(9)计算得到，其中6种组合的结果是0或1，而另外2种组合(001和110)的结果分别是-1和2，因此，hi的最终值可根据式(10)计算得到：

(10)

2 仿真数据验证

2.1 仿真数据

为了测试算法的寻优能力，作了如下仿真试验。样本数共281个，3类样本组成，这3类的样本数分别为93、108和80，特征维数为20，其中特征1和特征2是有效的分类特征，特征3至特征20的取值为0到1之间的随机数，对分类基本不起任何作用。各样本在特征1和2张成的空间的分布如图3(a)所示，特征3和特征4的分布如图3(b)，图3中每种颜色代表一种类别。显然，遗传优化的目标是得到最优特征组合11000000000000000000。

图3 仿真数据Fig.3 Simulation data

2.2 算法结果及分析

为了验证MEDEGA算法的性能，与其他3种算法进行比较,这3种算法分别是：差分遗传算法(Different Evolution and Genetic Algorithm，DEGA)、基于ReliefF的遗传算法(Genetic Algorithm based on ReliefF，RGA)、SGA。遗传算子设置如表1所示。

其他参数取值及说明如下：

1) 交叉率。取值过大会破坏群体中的优良模式，不利于进化，取值过小，产生新个体的速度较慢，一般建议取值范围是0.4～0.99[14]，本文交叉率取值为0.7。

表1 4种算法的遗传算子Table 1 Genetic operators in four algorithms

2) 变异率。取值较大可能会破坏很多较好的模式，取值太小则产生新个体的能力和抑制早熟现象能力较差，一般建议取值范围是0.000 1～0.1[14]，本文变异率取值为0.05。

算法共测试50次，每次运行100代。

2.2.1 研究算法的收敛速度

图4所示是在50次测试中选取各种算法最快找到最优特征组合的一次测试，并分别从4种种群规模为80、100、150和200对4种算法的收敛情况进行分析。从图中可得到，在不同的种群，MEDEGA都能最快找到最优解，基本都在10代以内就收敛到最优解；当在种群规模为80和100时，MEDEGA和DEGA找到最优解的速度相差不大，但和RGA或SGA差别就大；但当在种群规模为150和200时，4种算法的差别就没那么明显，但种群规模大，搜索时间就需要更多。因此，总体来看，MEDEGA在不同种群规模中收敛速度均是最快的。

图4 4种算法在不同种群规模的收敛曲线图Fig.4 Convergence graphs of different population sizes with four algorithms

2.2.2 种群均值情况

图5所示是在50次测试中选取各种算法最快找到最优特征组合的一次测试，分析种群均值情况。从图中可得到，MEDEGA和DEGA这两种算法种群均值比RGA和SGA的种群均值高很多，特别是MEDEGA，在进化初期比其他3种算法的种群均值都高，这说明在进化初期就能快速搜索到优秀的个体，并且将父代优秀的基因或基因模式学习并遗传给后代。

2.2.3 最优特征子集可靠性

从50次测试的角度对各种算法找到的最优特征子集可靠性进行分析。其中，表2中的“Frequency of the best feature subset”是指在50次测试中，成功找到最优特征组合“1100000000 0000000000”的次数；“Frequency of the optimum pattern”是指50次测试中成功找到特征最佳模式“11******************”的次数(“*”代表一个“0”或“1”)； “Solution speed”表示50次测试中成功找到最优特征组合的平均求解次数。

在表2中，从成功找到最优特征组合次数和求解速度这两个方面来看，MEDEGA和DEGA相差不太大，MEDEGA略优于DEGA，但MEDEGA和DEGA明显优于RGA和SGA；从找到最佳模式的次数来看，MEDEGA较其他3种算法具有明显的优势。由于在实际应用中，遗传算法的适应度函数设计要结合实际问题，综合考虑各方面的因素，并且往往有些方面是互相制约的。因此，为了避免偶然性或干扰性，增加找到解的可靠性及适用性，本文根据最优适应值所对应的特征组合，综合考虑50次测试中特征或特征组合出现次数。当某个特征或特征组合出现的次数越多，说明选中它们是更可靠的。因此，从结果来看，本文所采取的方法对提高解的可靠性和适用性是有效的。

图5 4种算法在不同种群规模的种群均值Fig.5 Average values of different population sizes with four algorithms

表2 可靠性和求解速度的比较数据Table 2 Comparison of reliability and solution speed

AlgorithmPopulationsizeFrequencyofthebestfeaturesubsetFrequencyoftheoptimumpatternSolutionspeedMEDEGA80174319100284415150224616200234312DEGA80223226100262821150202022200131317RGA80232901006285215014295920082746SGA8053671100532571505256720073246

综合以上图4、图5和表2的分析：图4和图5 是对50次测试中的一次测试进行比较分析，从种群收敛速度和种群均值这两个方面对算法的性能进行分析；表2则从50次测试进行总体分析。可以看出MEDEGA比其他3种算法表现得更优，这是因为MEDEGA算法以特征权值作为先验知识，对算法的搜索起到引导作用；另外，变异操作采用差分变异，将3个不同父代个体进行线性组合生成一个新的个体，这更利于将父代优秀的基因或基因模式学习并遗传给后代。同时，还综合考虑最优适应值及其对应特征或特征组合选中的次数，增加最终选出的特征组合的可靠性和适用性。另外，MEDEGA和DEGA在各方面的性能相差不大，但MEDEGA与RGA的性能相差比较大，说明差分变异与权值相比，差分变异对算法的性能改善作用更大。

3 滚动轴承故障特征选择

3.1 滚动轴承故障模拟实验

采用沈阳发动机设计研究所研制的带机匣的航空发动机转子试验器进行故障模拟实验[15]，分别在试验器垂直上方和水平方向布置加速度传感器，获取机匣的振动加速度信号，振动信号通过NI USB9234 数据采集器进行采集，加速度传感器信号为B&K 4805，采样频率为10.24 kHz，实验的对象为6206型滚动轴承，轴承参数如表3 所示，试验器如图6所示。分别在转速为1 500、1 800、2 000、2 400 r/min下进行了3组故障模拟试验，每组试验数据包括正常、外圈故障、内圈故障、以及滚动体故障4种状态(如图7所示)，每个转速下均有两个测点，其中CV为涡轮机匣垂直上方测点，CH为涡轮机匣水平方向测点。

利用时域、频域和时频分析法得到13个无量纲特征量[16]，13个无量纲特征量的符号定义为：歪度S1、波型因数S2、冲击指标S3、峰值指标S4、峭度S5、裕度指标S6、重心频率S7、均方频率S8、频率方差S9、内圈频率包络谱特征量S10、外圈频率包络谱特征量S11、滚动体频率包络谱特征量S12、以及保持架频率包络谱特征量S13。故障样本数据如表4所示，其中：“All CV”表示在转速1 500、1 800、2 000、2 400 r/min下，涡轮机匣垂直上方测点获得的样本数据；“1 500 CH”表示在转速1 500 r/min下，涡轮机匣水平方向测点获得的样本数据；其他数据集命名类似。

图6 航空发动机转子试验器Fig.6 Aero-engine rotor test rig

图7 故障加工后的6206型轴承Fig.7 Bearing 6206 after fault processing

表3 6206型轴承基本参数Table 3 Basic parameters of bearing 6206

mm

3.2 滚动轴承故障特征选择结果及分析

遗传算法的参数取值：群体规模为50，交叉率为0.7，变异率为0.05，式(6)中的t=0.5，缩放因子F=0.5。算法共测试50次，每次运行50代。

对表4的滚动轴承故障样本数据，利用ReliefF算法得到了13个特征的权值，如图8所示。通过图8(a)可以看出，在CV测点，特征9(即S9)的权值最大，即它对分类的重要性最大。而对于图8(b)即在CH测点，对所有的数据集来说，没有具体某个特征对分类的贡献是比较明显的，但相对来说，S9和S11对分类的贡献相对比较大。

表4 滚动轴承故障样本数据Table 4 Sample data sets of rolling bearing fault diagnosis

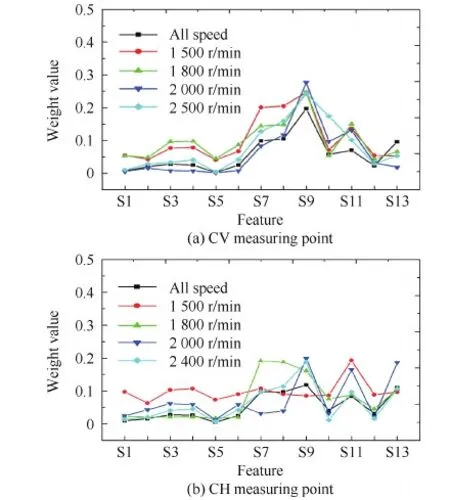
图8 特征权值Fig.8 Feature weight values

针对表4的滚动轴承故障样本数据，对所提取出的13个特征，分别利用4种算法进行特征选择，结果如表5所示。利用Weka软件对特征选择后的滚动轴承故障进行分类识别，其结果如图9 所示。在Weka软件里采用J48算法验证分类的准确率，10折交叉验证。

表54种算法找到的特征子集

Table5Selectedfeaturesubsetsobtainedbyfouralgorithms

DatasetAlgorithmMEDEGADEGARGASGAAllCV2,8,9,10,112,8,9,112,8,9,112,9,111500CV7,8,97,8,97,8,97,8,91800CV7,9,10,117,9,117,9,117,9,112000CV1,7,9,10,112,7,9,10,117,9,119,112400CV7,9,108,9,108,9,108,9,10AllCH2,7,9,11,122,8,9,10,112,8,9,118,9,111500CH2,8,9,112,8,9,112,8,9,118,9,111800CH7,8,9,117,8,9,117,8,97,8,9,112000CH7,8,9,11,132,8,9,117,9,119,112400CH8,9,11,127,9,117,9,118,9,11

图9 4种算法的分类准确率Fig.9 Classification accuracy by four algorithms

从表5和图9可以看出，MEDEGA找到的特征子集所对应的分类准确率要优于另外3种算法，除了1个数据集(All CH)比最高分类准确率低1.21%，其他的数据集，MEDEGA的分类准确率都优于或等于其他的算法(6个优于，3个等于)。并且，个别数据集是以相同的特征组合得到更高的分类准确率；有些数据集是特征子集稍多1～2个特征，得到更高的分类准确率，这说明MEDEGA具有更强的搜索能力，较好地改善了遗传算法的早熟现象。同时，从表5中可以看出，MEDEGA选出的特征也符合实际的应用。

3.3 滚动轴承故障特征选择中的收敛速度

为了验证算法在滚动轴承故障特征选择中的收敛速度，选取表5中的1 500 CV数据集作为研究对象，这是因为从表5可知4种算法只在这个数据集上找到的特征子集是相同的，因此，收敛速度的比较是基于各种算法达到的目标相同的情况下进行的。从图10中可以看出MEDEGA以更快的速度找到最优解。

图10 4种算法在数据集1 500 CV的收敛曲线图Fig.10 Convergence graph with four algorithms in dataset 1 500 CV

3.4 采用单准则与多准则的特征选择结果及分类准确率

比较本文算法MEDEGA(采用多准则融合)与采用单准则(ReliefF、基于类间类内距离)的特征选择方法的性能。它们找到的最优特征子集与分类准确率分别如表6和图11所示。其中，表6中“类间类内”得到的特征子集是将基于类间类内距离的准则与GA结合，类间类内距离作为GA的适应度函数。另外，考虑到比较的有效性，对于ReliefF，每个数据集按特征权重大小依次取靠前的特征，且特征个数与MEDEGA的特征个数相同。

表6单准则与多准则融合得到的特征子集

Table6Selectedfeaturesubsetsobtainedbysinglecriterionandmulti-criteria

DatasetAlgorithmMEDEGAReliefFInter-classandintra-classAllCV2,8,9,10,117,8,9,11,132,9,111500CV7,8,97,8,98,91800CV7,9,10,117,8,9,118,9,112000CV1,7,9,10,117,8,9,10,1110,112400CV7,9,108,9,108,9,10AllCH2,7,9,11,127,8,9,11,132,8,9,111500CH2,8,9,114,7,111,7,8,111800CH7,8,9,117,8,9,138,112000CH7,8,9,11,133,4,9,11,137,9,112400CH8,9,11,127,8,9,137,11

图11 单准则与多准则融合的分类准确率Fig.11 Classification accuracy by single criterion and multi-criteria

从图11可以看出，10组数据中，仅有2组数据的结果比ReliefF稍差，而比类间类内准则的结果均要好。由此可见，MEDEGA的分类准确率总体上要优于其他两种单准则的分类准确率，说明本文提出的多准则融合方法对提高特征子集的分类准确率是有效的。

4 结 论

1) 提出了一种用于特征选择的多准则融合的差分遗传算法，通过对选择算子和变异算子进行改进，既保证群体多样性，又提高了搜索速度，同时，采用多准则融合的评价准则，增强了解的可靠性。利用仿真实验对算法进行了验证，结果表明了方法的正确有效性。

2) 针对航空发动机转子试验器的滚动轴承故障实验数据，利用本文方法进行了故障特征选择研究，结果也表明了本文方法的有效性。

[1] 张学工. 模式识别[M]. 3版. 北京: 清华大学出版社, 2010: 157.

ZHANG X G. Pattern recognition[M]. 3rd ed. Beijing: Tsinghua University Press， 2010: 157 (in Chinese).

[2] AKRAM A, RAMI N, AHMED A A. Enhancing the diversity of genetic algorithm for improved feature selection[C]//2010 IEEE International Conference on Systems Man and Cybernetics (SMC). Piscataway, NJ: IEEE Press, 2011: 1325-1331.

[3] MAJID M, NICOLAS H Y. On the use of the genetic algorithm filter-based feature selection technique for satellite precipitation estimation[J]. IEEE Geoscience and Remote Sensing Letters, 2012, 9(5): 963-967.

[4] CANUTO A M P, NASCIMENTO D S C. A genetic-based approach to features selection for ensembles using a hybrid and adaptive fitness function[C]//The 2012 International Joint Conference on IEEE Neural Networks (IJCNN). Piscataway, NJ： IEEE Press, 2012: 1-8.

[5] 高鹏毅, 陈传波, 张葵, 等. 一种使用多Filter初始化GA种群的混合特征选择模型[J]. 小型微型计算机系统, 2012, 33(11): 2379-2384.

GAO P Y, CHEN C B, ZHANG K, et al. Hybrid model initializing the genetic population with multiple filters for feature selection[J]. Journal of Chinese Computer Systems, 2012, 33(11): 2379-2384 (in Chinese).

[6] 任江涛, 孙婧昊, 黄焕宇, 等. 一种基于信息增益及遗传算法的特征选择算法[J]. 计算机科学, 2006, 33(10): 193-195.

REN J T, SUN J H, HUANG H Y, et al. Feature selection based on information gain and GA[J]. Computer Science, 2006, 33(10): 193-195 (in Chinese).

[7] 陈果, 邓堰. 遗传算法特征选取中的几种适应度函数构造新方法及其应用[J]. 机械科学与技术, 2011, 30(1): 124-128.

CHEN G, DENG Y. Several new methods for features extraction based on genetic algorithm and their application[J]. Mechanical Science and Technology for Aerospace Engineering, 2011, 30(1): 124-128 (in Chinese).

[8] 刘元宁, 王刚, 朱晓冬, 等. 基于自适应多种群遗传算法的特征选择[J]. 吉林大学学报(工学版), 2011, 41(6): 1690-1693.

LIU Y N, WANG G, ZHU X D, et al. Feature selection based on adaptive multi-population genetic algorithm[J]. Journal of Jilin University (Engineering and Technology Edition), 2011, 41(6): 1690-1693 (in Chinese).

[9] KONONENKO I. Estimation attributes: Analysis and extensions of ReliefF[C]//Proceedings of the 1994 European Conference on Machine Learning, 1994: 171-182.

[10] 张丽新, 王家廞, 赵雁南, 等. 基于Relief的组合式特征选择[J]. 复旦学报(自然科学版), 2004, 43(5): 893-898.

ZHANG L X, WANG J X, ZHAO Y N, et al. Combination feature selection based on Relief[J]. Journal of Fudan University (Natural Science), 2004, 43(5): 893-898 (in Chinese).

[11] 杨启文, 蒋静坪, 曲朝霞, 等. 应用逻辑操作改善遗传算法性能[J]. 控制与决策, 2000, 15(4): 510-512.

YANG Q W, JIANG J P, QU Z X, et al. Improving genetic algorithms by using logic operation[J]. Control and Decision, 2000, 15(4): 510-512 (in Chinese).

[12] DENG C, ZHAO B, YANG Y, et al. Binary encoding differential evolution for combinatorial optimization problems[C]//Proceedings of the 2011 Third International Workshop on Education Technology and Computer Science, 2011: 11-14.

[13] 刘琛, 林盈, 胡晓敏. 差分演化算法各种更新策略的对比分析[J]. 计算机科学与探索, 2013, 7(11): 983-993.

LIU C, LIN Y, HU X M. Analyses and comparisons of different update strategies for differential evolution[J]. Journal of Frontiers of Computer Science and Technology, 2013, 7(11): 983-993 (in Chinese).

[14] 周明. 遗传算法原理及应用[M]. 北京: 国防工业出版社, 1999: 59.

ZHOU M. Genetic algorithms: Theory and applications[M]. Beijing: National Defense Industry Press, 1999: 59 (in Chinese).

[15] 陈果, 郝腾飞, 程小勇, 等. 基于机匣测点信号的航空发动机滚动轴承故障诊断灵敏性分析[J]. 航空动力学报, 2014, 29(12): 2874-2884.

CHEN G, HAO T F, CHENG X Y, et al. Sensitivity analysis of fault diagnosis of aero-engine rolling bearing based on vibration signal measured on casing[J]. Journal of Aerospace Power, 2014, 29(12): 2874-2884 (in Chinese).

[16] 梅宏斌. 滚动轴承振动监测与诊断[M]. 北京: 机械工业出版社, 1995.

MEI H B. Rolling bearing vibration monitoring and diagnosis[M]. Beijing: China Machine Press, 1995 (in Chinese).

关晓颖女， 博士研究生。主要研究方向： 智能计算、 遗传算法、 模式识别及故障诊断。

Tel.: 025-84891850

E-mail: xiaoying_close@sina.com

陈果男， 博士， 教授， 博士生导师。主要研究方向： 航空发动机智能诊断及专家系统， 航空发动机整机振动与转子动力学、 故障诊断。

Tel.: 025-84891850

E-mail: cgzyx@263.net

林桐男， 硕士研究生。主要研究方向： 航空发动机状态检测与故障诊断技术。

Tel.: 025-84891850

E-mail: nuaa_lintong@163.com

*Correspondingauthor.Tel.：025-84891850E-mail:cgzyx@263.net

Featureselectionmethodbasedondifferentialevolutionandgeneticalgorithmwithmulti-criteriaevaluationanditsapplications

GUANXiaoying,CHENGuo*,LINTong

CollegeofCivilAviation,NanjingUniversityofAeronauticsandAstronautics,Nanjing210016,China

Inordertomakeawholeevaluationtotheselectedfeaturesubset,whichimprovesthereliabilityofthebestsubsetandthespeedofitssearching,thepaperpresentsanovelfeaturemethodbasedondifferentialevolutionandgeneticalgorithmwithmulti-criteriaevaluation.Thisalgorithmisusedtoevaluatethefeaturesubsetbythemulti-criteriaevaluation.Meanwhile,theimprovedgeneticoperatorswereproposed,whichimprovestheselectionoperatorandthemutationoperator.Designingtheselectionoperatorwithacombinationoffeatureweightvaluesandfitnessisbeneficialtoselectingtheindividualswhichcontainthehighfitnessandimportantfeaturesfromthepopulation.Inaddition,itintroducesdifferentialstrategytoimprovemutationoperator,whichimprovesthediversityofevolutionpopulationandsearchingefficiency.Finally,simulationexampleteststhevalidityoftheproposedalgorithm.Thevalidityoftheproposedmethodisalsoverifiedwithrollingbearingfaultdiagnosis.

featureselection;multi-criteria;differentialevolution;geneticalgorithm;rollingbearing;faultdiagnosis

2015-11-19；Revised2016-01-14；Accepted2016-01-29；Publishedonline2016-02-021627

URL：www.cnki.net/kcms/detail/11.1929.V.20160202.1627.004.html

NationalNaturalScienceFoundationofChina(61179057)

2015-11-19；退修日期2016-01-14；录用日期2016-01-29； < class="emphasis_bold">网络出版时间

时间：2016-02-021627

www.cnki.net/kcms/detail/11.1929.V.20160202.1627.004.html

国家自然科学基金 (61179057)

*

.Tel.：025-84891850E-mailcgzyx@263.net

关晓颖， 陈果， 林桐． 特征选择的多准则融合差分遗传算法及其应用J． 航空学报,2016,37(11):3455-3465.GUANXY，CHENG，LINT.Featureselectionmethodbasedondifferentialevolutionandgeneticalgorithmwithmulti-criteriaevaluationanditsapplicationsJ.ActaAeronauticaetAstronauticaSinica,2016,37(11):3455-3465.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2016.0036

V263.6

A

1000-6893(2016)11-3455-11