弹性飞机跨声速机动载荷计算方法
张辉, 李杰
西北工业大学 航空学院, 西安 710072
弹性飞机跨声速机动载荷计算方法
张辉, 李杰*
西北工业大学 航空学院, 西安 710072
基于跨声速非定常气动力求解的重叠场源法,开展了弹性飞机跨声速机动载荷计算方法研究,为现代飞机结构强度设计提供更加可靠和精确的临界载荷计算方法。首先通过采用重叠场源法求解关于62%根弦俯仰振荡的LANN机翼在马赫数为0.822的非定常气动力并与实验结果进行对比,验证了重叠场源法对跨声速激波效应预测和非定常气动力计算的能力;其次应用频域气动力有理近似技术拟合场源法计算得到的广义气动力系数矩阵,建立了机动载荷分析的状态空间模型;然后完成了某型民用飞机俯仰机动载荷分析,研究了俯仰机动飞行情况下飞机机体状态量及飞机部件载荷响应规律。计算结果表明:考虑机体弹性变形后,机翼和平尾气动载荷响应最大值分别减小了5.1%和10.6%,升降舵气动载荷响应最大值增大了16.2%,在飞机结构强度设计中必须考虑机体弹性效应对飞机部件载荷的影响。
机动载荷; 非定常气动力; 气动力影响系数矩阵; 跨声速; 重叠场源法
飞机飞行载荷是飞机结构设计的依据,飞机载荷计算的准确程度直接决定了强度分析的准确性和结构设计的可靠性,同时载荷计算的准确有利于减小飞机结构重量,提高飞机使用的经济性。然而现代飞机飞行载荷的精确计算面临着巨大的挑战,一方面,现代飞机的飞行速度大大提高,对于民用客机如A380、波音787等,其巡航马赫数都已超过0.8,对于战斗机如F22以及中国的歼10等均已实现超声速巡航,这使得飞机部件严重受载情况经常发生在跨声速飞行条件,在跨声速飞行条件下激波效应引起的气动力非线性明显增强,在飞机机动飞行达到较大迎角时出现翼面流动分离,将进一步增强气动力非线性特征,长期以来用于机动载荷分析所建立的线性气动力方法不能有效预测气动力的非线性特性,很大程度地影响了机动载荷计算的精度。另一方面,现代飞机设计在追求高巡航、超机动和敏捷性的同时又要求飞机具有较低的结构重量系数和较长的机体寿命,因而现代飞机设计往往降低了对飞机结构的刚性要求,广泛采用轻质的新型复合材料[1],这使得气动弹性效应对机动载荷的影响逐渐明显,引起翼面的弯矩、扭矩及剪力发生较大变化,机动载荷计算必须考虑气动弹性变形的影响。
围绕弹性飞机的机动载荷计算问题,国外研究者Kier[2]比较了用于机动载荷分析的准定常涡格法、改进的片条理论以及基于偶极子格网法的有理函数逼近3种非定常气动力模型对载荷计算的影响;Petersson等[3]的研究得到了由非线性刚体气动力模型和线性气动弹性模型组成的弹性飞机耦合计算模型用来计算给定飞行条件下飞机结构的静气动弹性载荷,并将计算得到的载荷用来进行飞机结构优化设计研究;Raveh[4]发展了一种基于计算流体力学(CFD)方法的超静定气动弹性配平系统的优化方法,利用迎角、平尾偏度及机翼控制面偏转配平飞机,该方法提供了计算跨声速范围内非线性静气动弹性载荷的方法;Flansburg[5]研究了AMC-X运输机构型临界机动载荷的模拟方法,气动力采用了势流面元理论,与传统的机动载荷求解方法相比,该模拟方法实现了机动模拟和载荷计算的耦合求解。Meirovitch和Tuzcu[6]研究了飞行中的弹性飞机对初始条件和外部激励响应的计算模拟,发展了针对弹性飞机动力学机动和控制问题统一的描述形式,可综合考虑弹性飞机的结构、气动和控制等因素,其气动力求解方法采用片条理论,这使得计算效率很高,但同时限制了其适用范围。国内彭小忠和邱传仁[7-10]关于大型飞机载荷计算进行了较全面的研究,研究了飞机运动参数及总载荷求解、飞机部件分布载荷计算方法、载荷计算中的气动弹性修正方法和载荷临界情况筛选方法等,为国内大型飞机载荷计算提供了重要的技术参考。杨超等[11]提出了一种可同时考虑结构几何非线性和曲面气动力效应的大变形飞机静气动弹性配平和载荷分析方法,该方法利用三维曲面涡格法计算大变形飞机的曲面气动力,引入非线性结构有限元计算方法考虑结构几何非线性,采用曲面样条插值方法解决气动/结构耦合问题。通过对国内外关于弹性飞机机动载荷计算的相关文献的调研发现,目前国外研究者对综合考虑弹性飞机的结构、气动和控制因素的耦合求解机动载荷的方法关注较多,气动力求解方法开始逐渐采用非线性方法;国内研究者对弹性飞机平衡机动载荷的计算研究较多,考虑了气动力非线性的影响并采用了耦合求解气动/结构的方法进行静气动弹性载荷分析,但对于动力学机动载荷计算还仍按照传统的非耦合方法,弹性变形的影响主要通过弹性修正进行处理。
本文基于重叠场源法[12]进行跨声速非定常气动力计算,生成气动力影响系数(Aerodynamic Influence Coefficient, AIC)矩阵,利用目前已经发展较完备的基于AIC矩阵的气动弹性分析方法,通过建立机动载荷计算的状态空间模型,发展了一种适用于跨声速范围内弹性飞机机动载荷计算的方法。
1 气动力求解方法
面元方法能够处理复杂构型,可以提供较精确的气动力,更重要的是可生成AIC矩阵,该矩阵被认为是工业气动弹性设计过程中的关键基础之一[13]。然而对于跨声速流动,通常认为面元方法是不适用的,因为它不能考虑跨声速激波效应。近年来,CFD方法[14]通过求解Euler或Navier-Stokes(NS)方程可提供精确的跨声速解,但是它不能生成AIC矩阵,不能有效地应用于常规的气动弹性分析中。Liu等[15]的研究已经表明:如果将高精度CFD方法得到的定常流动解引入跨声速小扰动方程,跨声速激波效应即可被考虑到,基于该思想Chen等[12]发展了重叠场源方法并用于气动弹性分析。图1给出了本文建立的基于重叠场源法求解时间线化的跨声速小扰动(Time-Linearized Transonic Small Disturbance TLTSD)方程生成AIC矩阵的流程框图。

图1 非定常气动力求解流程框图Fig.1 Flowchart of solving unsteady aerodynamics
1.1 基于雷诺平均NS方程的定常流动数值方法
基于雷诺平均NS(RANS)方程数值求解的控制方程为
(1)
式中:Q=[ρρuρvρwρe]T为守恒向量,ρ、e和(u,v,w)分别为密度、单位质量气体的总能量和直角坐标系下的速度分量;Ω为控制体体积;S为控制体表面矢量;F和FV分别为通过表面S的无黏通量和黏性通量。空间无黏项采用三阶迎风MUSCL(Monotonic Upstream-centered Scheme for Conservation Laws)插值的Roe格式,黏性项采用中心差分格式离散,采用隐式LU-SGS(Lower-Upper Symmetric Gauss-Seidel)方法进行时间推进,选用Spalart-Allmaras(SA)湍流模型,通过多重网格技术来加速收敛[16]。
1.2 跨声速小扰动积分方程
由结构振荡幅值线化非线性跨声速小扰动方程得到TLTSD方程[17],即

(2)

φ(xo,yo,zo)=φs+φv+φshock
(3)
φs为表面面元强度对速度势的影响,可写为
(4)

φv为体源对速度势的影响,φshock为激波面对速度势的影响,可分别写为
(5)
(6)
式中:Δσv为穿过激波面体源强度的跳跃;dS为激波面面元。当不存在跨声速激波时,Δσv=0,φshock自动消失。另外,当激波出现时,也可通过对φv完成如下分部积分运算以消掉φshock。
(7)
得到
(8)
式中:xs为激波位置;ε为激波面无限小厚度。由式(6)和式(8)可得
(9)
1.3 场源模型的建立及流场数值解的插值
针对复杂飞机构型,建立气动模型需要将其分为翼面类和机身类部件处理。翼面类部件为薄面,其展向截面可由翼面厚度分布表示,这类部件包括机翼、平尾、垂尾和挂架等,由位于翼面类部件均平面的非定常涡面来模拟;机身类部件为非升力面类的体,如机身、发动机短舱、导弹弹体以及副油箱等,机身类部件表面离散为体表单元,每个体表单元上布置非定常源以模拟由于体的体积效应产生的气动力分布。围绕翼面类部件或机身类部件定义体块,然后将体块分割为若干体单元,完成场源模型的建立。
建立了合适的场源模型后,将基于RANS方程的定常流场数值解插值到场源模型的各个体单元上,从而考虑跨声速激波效应对非定常气动力计算的影响。因为CFD计算网格单元分布比场源模型的体单元分布密集得多,所以CFD结果到场源体单元的插值可以通过如下步骤完成:
步骤1选择需要插值的场源模型体块,记为VOLUME_i。
步骤2建立场源模型的体块与CFD网格块的关系,确定与场源模型对应的网格块,记为BLOCK_i。
步骤3选择VOLUME_i内需要插值的体单元CELL_i。
步骤4在网格块BLOCK_i内,计算并搜索距离CELL_i最近的CFD网格点,记为GRID_INTER。
步骤5将CFD网格点GRID_INTER的数据信息赋值给CELL_i体单元控制点。
步骤6重复步骤1~步骤5,完成某一体块内所有体单元的插值。
步骤7重复步骤1~步骤6,完成场源模型所有体单元的插值。
1.4 跨声速非定常气动力计算算例
20世纪80年代美国空军莱特航空实验室(Air Force Wright Aeronautical Laboratories,AFWAL)针对LANN机翼进行了一系列的超临界机翼跨声速实验研究,实验在NLR 2 m×1.6 m 跨声速风洞中完成,实验马赫数从0.62到0.95覆盖了大部分跨声速飞行范围,基于平均气动弦长的雷诺数约为5.0×106,LANN机翼模型可绕62%根弦做俯仰振荡,减缩频率在0~0.3之间变化,振幅约为0.25°,AFWAL-TR-83-3050[18]研究报告给出了详细的定常和非定常压力分布实验结果,本节以LANN机翼为计算算例验证本文非定常气动力求解方法的可靠性。
LANN机翼为中等展弦比跨声速机翼构型,配置12%厚度超临界翼型,半展长为1 m,翼根弦长为0.361 m,翼尖弦长为0.181 m,1/4弦线后掠角为25°,从翼根到翼尖扭转4.8°。图2给出了本文采用的LANN机翼表面网格,整个计算域内网格节点约为100万。计算状态取马赫数Ma=0.822,迎角α=0.6°。LANN机翼展向位置η=47.5%和η=65.0%翼面压力系数Cp分布的计算结果(Cal.)与实验结果(Exp.)[18]对比如图3所示。由图3可见,在展向位置η=47.5%计算对机翼上表面激波位置的预测与实验结果相比稍靠后,在展向位置η=65.0%计算结果与实验结果吻合较好。由此可见本文基于RANS方程的数值求解程序能够有效地对跨声速流动进行数值模拟,可以较好地预测机翼表面跨声速激波位置及强度。本文基于RANS方程的数值求解程序的计算精度与当前主流的CFD数值求解方法相当,可以作为重叠场源法求解非定常气动力的背景流场,为下文基于重叠场源法的非定常气动力计算奠定了基础。

图2 LANN机翼表面网格Fig.2 LANN wing surface mesh

图3 LANN机翼压力系数分布的计算与实验结果对比Fig.3 Comparison of steady pressure coefficient distribution between calculable and experimental results on a LANN wing
建立LANN机翼场源模型如图4所示,依据文中给出的插值步骤,将基于RANS方程的数值计算结果插值到该场源模型的体单元,然后通过求解跨声速小扰动方程以得到翼面非定常气动力结果。图5给出了LANN翼面绕62%根弦俯仰振荡的(展向位置η=47.5%和η=65.0%处)本文计算所得非定常压力系数分布结果与实验结果[18]的对比,可见本文跨声速非定常气动力计算方法对η=47.5%处激波位置的预测与实验结果相比略微靠后,约在翼面弦向34%位置附近,η=65.0%处非定常压力系数计算结果与实验结果吻合较好,激波位置约在翼面弦向39%附近。这与定常流动数值解预测的激波位置是一致的,说明本文所用CFD流场数值解到场源体单元的插值方法可靠,非定常激波位置和强度由定常流场数值解确定。图5中同时给出了基于偶极子格网法(Doublet Lattice Method, DLM)的计算结果,对比可见,DLM线性方法完全不能模拟跨声速激波效应。

图4 LANN机翼场源模型Fig.4 Field-panel model of LANN wing

图5 LANN翼面绕62%根弦俯仰振荡的非定常压力系数Fig.5 Unsteady pressure coefficient on a LANN wing caused by pitch oscillation about 62% root chord
2 机动载荷分析方法
2.1 机动载荷分析的时域方程
对于机动载荷分析,气动控制面产生气动力的情形有3种:① 控制系统激励气动控制面;② 飞行员操纵控制面偏转;③ 飞机配平所需的控制面偏转。考虑这3种情形气动控制面产生的气动力,机动载荷分析的时域矩阵方程为[19]
(10)
式中:Mhh、Bhh和Khh分别为广义质量矩阵、广义阻尼矩阵和广义刚度矩阵;ξ为飞机刚体模态及弹性模态构成的广义模态坐标向量;P0为飞机配平控制面偏转产生的气动力,即
P0=q∞Q0δtrim
(11)
式中:q∞为动压;Q0为飞行员操纵控制面初始配平条件引起的广义气动力系数矩阵;δtrim为控制面偏角矢量。Ph(t)包括了飞机机体引起的气动力、控制系统激励控制面偏转引起的气动力和飞行员操纵控制面偏转引起的气动力,将Ph(t)转换到频域内,可写为
Ph(iω)=-q∞Qhh(ik)ξ(iω)-
q∞Qhc(ik)δc(iω)-q∞QhP(ik)δP(iω)
(12)
式中:Qhh为飞机机体引起的广义气动力;Qhc为控制系统激励控制面偏转引起的气动力;δc为控制系统激励控制面的偏转角;δP为飞行员操纵控制面的偏转角。
2.2 机动载荷分析的状态空间建模
机动载荷分析研究,由于飞行员操纵引起的弹性飞机瞬态载荷响应问题,将飞行员操纵控制面产生的气动力处理为外部力,弹性飞机机动载荷响应问题就与气动伺服弹性响应问题类似,这样就可以利用求解气动伺服弹性(Aeroservoelasticity, ASE)问题的方法研究弹性飞机的机动载荷响应问题。状态空间法已经广泛应用于时域气动伺服弹性分析[20-22],根据研究ASE问题的状态空间建模方法建立适用于机动载荷分析的状态空间模型,利用频域非定常气动力 (Unsteady Aerodynamic Force, UAF)有理近似方法[23]拟合广义气动力系数矩阵并将其延拓到复数域,其表达式为
[Qhh|Qhc|QhP]=[Ah,0|Ac,0|AP,0]+
[Ah,1|Ac,1|AP,1](b/V)s+
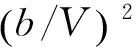
(13)
引入气动力滞后根扩增的扩充向量:
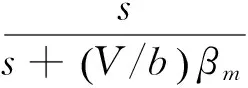
(14)
将式(10)通过拉普拉斯变换到复数域,并将式(13)和式(14)代入可得机体结构在气动力作用下运动方程的状态空间方程,即
(15)
式中:
2.3 机体状态坐标系下的状态空间模型
广义坐标ξ可写为广义刚体模态坐标xq和广义弹性模态坐标xe,即

对于自由飞行状态,即自由-自由边界条件下的飞机,刚体模态坐标为
xq=[q1q2…q6]
通常,模态坐标定义在进行结构有限元分析的主轴系中,主轴系与体轴系的定义一般相差一个俯仰角。在这两个坐标轴系内分别定义包含6个刚体自由度的刚体模态矩阵Rp和RB,这样主轴系到体轴系的转换关系为
进一步,将机体坐标系中的刚体自由度转换为机体状态量。对于对称飞行条件,机体状态量xAS=[xhθuαq],x为x轴方向扰动位移,h为z轴方向扰动位移,θ为扰动俯仰角,u为x轴方向扰动速度,α为扰动迎角,q为扰动俯仰速率。xAS和xR之间的转换关系[24]可写为
(16)
式中:Tx和Tz分别为x轴和z轴方向的位移;Ry为y轴方向的角位移。对于反对称飞行条件,xAS=[yβprφψ],其中,y为横侧向扰动位移,β为扰动侧滑角,p为扰动滚转角速率,r为扰动偏航角速率,φ为扰动滚转角,ψ为扰动偏航角。xAS和xR之间的转换关系[24]可写为
(17)
式中:Ty为y轴方向的位移;Rx和Rz分别为x轴和z轴的角位移。对于非对称机动飞行条件,转换矩阵即为以式(16)和式(17)转换矩阵为子矩阵的12×12阶矩阵。将变换关系代入式(15)得到状态空间方程,即
(18)
式中:ARR、ARξ、Aξξ、BRR和BRξ为状态空间模型系数矩阵,由上述转换关系得到。
3 某型飞机机动载荷计算分析
以国内某民用大型飞机为例,进行俯仰机动载荷计算分析,重点关注了其飞行包线内高马赫数状态下的载荷情况,气动力求解采用第1节介绍的重叠场源法,研究了俯仰机动飞行情况下飞机机体状态量及部件载荷的响应规律,同时考虑了机体弹性效应对飞机机动载荷的影响,为飞机结构强度设计提供参考依据。
3.1 计算模型
该飞机为翼吊式短舱布局,机翼为大展弦比、后掠式平面形状,其几何参数、重量及惯性矩如表1 所示。

表1 几何参数和质量特性Table 1 Geometrical parameters and mass property
气动力求解需要引入高精度的CFD定常流场数值解,并建立场源模型,将CFD数值解插值到场源模型,通过求解跨声速小扰动方程得到气动力影响系数矩阵,为进一步的机动载荷分析提供基础。图6(a)给出了该飞机CFD数值计算网格,整个流场计算域分割为32块,网格节点数约为600万;分别针对机身、机翼、平尾、垂尾及发动机短舱独立生成体单元以建立重叠场源模型,如图6(b)所示。

图6 气动模型Fig.6 Aerodynamic model
为了考虑机体结构弹性变形对机动载荷分析的影响,建立图7所示的结构模型,结构模型采用简单梁单元模拟,质量分布由CONM2卡片给出,基于Nastran模态分析模块求解飞机的结构总体质量阵,总体刚度阵和结构模态振型。

图7 结构有限元模型Fig.7 Structural finite element model
3.2 俯仰机动载荷分析
俯仰机动是飞机机翼、平尾和升降舵的严重载荷情况之一,飞行员通过操纵升降舵的偏转控制飞机进行俯仰机动飞行,升降舵的偏转规律通常包括了三角形输入、梯形输入和反梯形输入3种类型,升降舵偏转的具体时间历程根据飞机达到规定过载系数确定。作为俯仰机动载荷计算分析的方法验证,本节仅采用了升降舵的梯形输入,升降舵偏转角δe的时间t历程如图8(a)所示,从 0 s 开始,升降舵以40 (°)/s的偏转角速度上偏10°,随后保持至0.95 s,然后回舵至初始配平升降舵偏转角度。计算马赫数为0.80时俯仰机动过程中机体状态量以及机翼、平尾和升降舵承受的气动载荷在上述升降舵偏转规律下的响应时间历程如图8(b)~图8(f)。图中红色实线为采用刚体模型计算的结果,绿色点划线为采用弹性模型计算的结果。
俯仰机动的初始飞行状态为1g稳定水平直线飞行,表2给出了1g过载状态时静气动弹性配平变量值,该配平结果作为俯仰机动载荷计算分析的初始条件。

表2 1g过载时飞机静气动弹性配平结果Table 2 Trim variables value for aircraft with 1g load
由图8可以看到,对于不考虑机体弹性效应的刚性模型,在图8(a)所示的升降舵偏转角输入下,迎角从2.11°快速增大,在1.43 s附近达到最大值5.92°,随后振荡趋于稳定;俯仰角速度q在大约0.97 s内从0 (°)/s快速增大到5.53 (°)/s;平尾和升降舵气动载荷(FTail和FElevator)在0.30 s附近达到最大,分别为-74 857 N和-25 528 N,在0.30 s~0.95 s内平尾和升降舵气动载荷均稍有减小,回舵后,平尾承受的法向气动载荷快速减小,其中一段时间内承受的气动载荷方向变为向上,原因是该时间段内飞机正向俯仰角速度较大,由此引起平尾区域气流的上洗使得平尾有效迎角明显增大,平尾气动载荷随之而变。机翼气动载荷的响应时间历程与迎角的变化规律相似,1.43 s时机翼承受的气动载荷FWing最大,约为607 509 N,机翼载荷最大状态明显滞后于平尾及升降舵最大载荷状态;对比图8中实线和点划线可见,考虑机体弹性效应后,飞机俯仰机动机体状态量和飞机各个部件载荷响应时间历程基本相似,区别仅在于量值大小,与刚性模型的计算结果相比,迎角和俯仰角速度响应的最大值分别增大了0.47° 和0.12 (°)/s,机翼和平尾气动载荷响应最大值分别减小了5.1% (31 170 N)和10.6% (7 965 N),而升降舵气动载荷响应最大值增大了16.2% (4 127 N),引起这种变化的主要原因是俯仰机动的初始状态1g过载时弹性模型需要的升降舵配平角度明显大于刚性模型对应的升降舵配平角,在此基础上计算输入相同的升降舵偏转规律图8(a)后,在升降舵承受气动载荷最严重时,弹性模型的升降舵偏角为-14.04°,而刚性模型只有-11.34°。

图8 机体状态量和部件载荷响应历程Fig.8 Flight dynamic response of airframe states and component loads
图9给出了飞机俯仰机动中平尾及升降舵最大载荷状态时弹性与刚性模型压力系数分布的比较,该状态下整个平尾区域内压力系数均为负值,升降舵范围内的压力系数负值明显增大,这符合真实物理机理,首先飞机俯仰机动平尾及升降舵达到最大载荷状态时,升降舵正处于向上的最大偏转位置,升降舵区域的当地迎角为较大的负值,升降舵必定承受向下的较大气动载荷,其次偏转升降舵引起的气流扰动不是只限于升降舵操纵面,该扰动将扩及整个平尾翼面使得整个翼面压力系数分布发生改变。此外,与刚性模型相比,弹性模型机翼压力系数明显变小,与机翼气动载荷变化趋势一致,这种变化主要由机翼发生的负扭转弹性变形引起。
图10给出了飞机俯仰机动机翼最大载荷状态时弹性与刚性模型压力系数分布的比较,与图9 相比,无论是刚性模型还是弹性模型,该状态下的压力系数均明显增加,由图8(d)可知该状态下刚性模型和弹性模型机翼气动载荷比图9对应状态分别增大了266 760 N和277 590 N,此处机翼载荷的增大主要是俯仰机动中迎角响应的结果;除去升降舵的平尾区域内的压力系数不再全是负值,并且可以看出弹性模型的压力系数比刚性模型的压力系数偏大,平尾压力系数分布变化的原因一方面是随着飞机迎角的增大,平尾有效迎角相应增加,另一方面机体弹性效应的影响使得机身发生弯曲变形,从而引起平尾的有效迎角进一步增大,使得弹性模型的压力系数比刚性模型的压力系数偏大,此外,弹性模型升降舵区域内的压力系数与刚性模型相比更小,这与图8(f)升降舵载荷响应历程对比结果一致,主要是弹性模型和刚性模型不同的升降舵配平偏转角度引起的。

图9 平尾及升降舵载荷最大状态时弹性与刚性模型压力系数分布的比较Fig.9 Comparison of pressure coefficient contours obtained by rigid and flexible models when loads on tail/elevator reach maximum
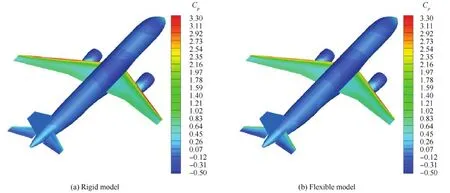
图10 机翼载荷最大状态时弹性与刚性模型压力系数分布的比较Fig.10 Comparison of pressure coefficient contours obtained by rigid and flexible model when loads on wing reach maximum
图11和图12分别给出了飞机俯仰机动升降舵和平尾最大载荷状态时以及机翼最大载荷状态时的气动弹性变形,由图可见机翼与机身均发生了明显的弯曲变形,机身的弯曲变形使得平尾向下偏转,其有效迎角增大,这与上一部分关于弹性变形对平尾压力分布影响分析的结论相吻合。图13 和图14分别给出了平尾以及升降舵最大载荷状态时和机翼最大载荷状态时机翼弹性主梁弯曲位移Tz和扭转角度θ沿着机翼展向y/c的分布,两个载荷状态下机翼翼尖上翘分别约0.63 m和0.48 m,机翼最大载荷状态时机翼的弯曲变形更大,两个载荷状态下机翼的扭转角均为负值,扭转角在内翼范围内变化较剧烈,在外翼范围内变化较平缓,机翼最大载荷状态时机翼的扭转变形较大,但是,考虑弹性变形后,在平尾及升降舵最大载荷状态时,机翼气动载荷减小了约12.3%,而在机翼最大载荷状态时,机翼气动载荷只减小了5.1%。究其原因,由图8(b)俯仰机动迎角响应历程可以得到,弹性变形使得飞机的迎角响应增大,在平尾及升降舵最大载荷状态时,弹性变形引起的迎角响应增大了0.29°,而在机翼最大载荷状态时,弹性变形引起的迎角响应增大了0.47°,综合弹性变形引起的迎角和机翼扭转角结果可以看到,在平尾及升降舵最大载荷状态时弹性变形对机翼载荷的影响更大。由此可见,两个载荷状态下弹性变形对机翼载荷的影响是合理的。
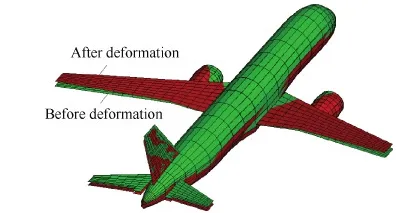
图11 平尾及升降舵载荷最大状态时气动弹性变形Fig.11 Aeroelastic deformation when loads on tail/elevator reach maximum

图12 机翼载荷最大状态时气动弹性变形Fig.12 Aeroelastic deformation when loads on wing reach maximum
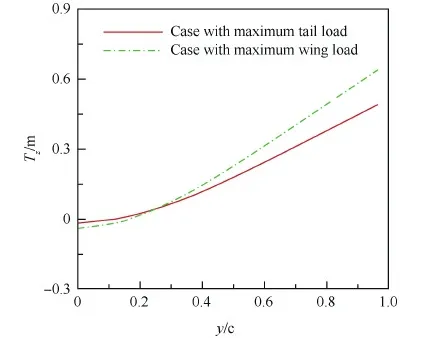
图13 两种载荷最大状态时机翼弹性主梁弯曲变形对比Fig.13 Comparison between two load maximum cases for bending deformation of elastic beam of wing

图14 两种载荷最大状态时机翼弹性主梁扭转变形对比Fig.14 Comparison between two load maximum cases for torsional deformation of elastic beam of wing
4 结 论
气动力求解采用重叠场源法,建立机动载荷分析的状态空间模型,完成了某型飞机跨声速俯仰机动载荷计算分析。
1) 重叠场源法可以有效地预测翼面跨声速激波位置和强度,适用于跨声速非定常气动力的求解,并且能够生成气动力影响系数矩阵,便于进一步的气动弹性应用。
2) 计算得到了俯仰机动过程中机翼、平尾和升降舵的严重载荷情况,当升降舵向上偏转到最大角度时,升降舵和平尾承受的载荷达到最大,而机翼最大载荷状态则相对滞后。
3) 机体弹性效应对飞机各个部件载荷均有一定程度的影响,考虑机体弹性变形后,机翼和平尾气动载荷响应最大值分别减小了5.1%和10.6%,而升降舵气动载荷响应最大值增大了16.2%;机身的弯曲变形引起平尾的偏转,使得平尾有效迎角增大,随着飞机迎角的增大,机身弯曲变形增大,机身弯曲变形引起平尾有效迎角的变化就越大,因而在飞机响应到较大迎角时,机身的弯曲变形对平尾载荷的影响必须重点考虑;此外,在考虑机体弹性效应对俯仰机动中飞机翼面载荷的影响时,需要综合考虑弹性变形引起的迎角响应效应和翼面扭转效应。
[1] 万志强, 唐长虹, 邹丛青. 柔性复合材料前掠翼飞机静气动弹性分析[J]. 复合材料学报, 2002, 19(5): 118-124.
WAN Z Q, TANG C H, ZOU C Q. Static aeroelastic characteristics analysis of a flexible forward-sweep composite aircraft[J]. Acta Materiae Compositae Sinica, 2002, 19(5): 118-124 (in Chinese).
[2] KIER T M. Comparison of unsteady aerodynamic modelling methodologies with respect to flight loads analysis: AIAA-2005-6027[R]. Reston: AIAA, 2005.
[3] PETERSSON O, LEITNER M, STROSCHER F. Structure optimization framework for aircraft subject to transient maneuver and gust loads: AIAA-2010-9122[R]. Reston: AIAA, 2010.
[4] RAVEH D E. Maneuver load analysis of overdetermined trim systems: AIAA-2007-1985[R]. Reston: AIAA, 2007.
[5] FLANSBURG B. Maneuver loads simulation for an advanced transport aircraft: AIAA-2008-1906[R]. Reston: AIAA, 2008.
[6] MEIROVITCH L, TUZCU I. Time simulations of the response of maneuvering flexible aircraft[J]. Journal of Guidance, and Dynamics, 2004, 27(5): 814-828.
[7] 彭小忠. 大型飞机飞行载荷计算方法[J]. 民用飞机设计与研究, 2004(3): 12-20.
PENG X Z. Calculation method about flight loads of large aircraft[J]. Civil Aircraft Design and Research, 2004(3): 12-20 (in Chinese).
[8] 彭小忠, 邱传仁. 大型飞机载荷计算中的气动弹性修正方法[J]. 民用飞机设计与研究, 1998(1): 8-14.
PENG X Z, QIU C R. Correction method for flight loads of large aircraft considering aeroelastics[J]. Civil Aircraft Design and Research, 1998(1): 8-14 (in Chinese).
[9] 彭小忠, 邱传仁. 飞机载荷临界情况筛选方法[J]. 民用飞机设计与研究, 1998(2): 17-22.
PENG X Z, QIU C R. Method of screening critical loads of aircraft[J]. Civil Aircraft Design and Research, 1998(2): 17-22 (in Chinese).
[10] 彭小忠, 邱传仁. 大型运输类飞机部件分布载荷计算方法[J]. 民用飞机设计与研究, 1999(2): 11-19.
PENG X Z, QIU C R. Calculation method on distribution loads of large transport aircraft[J]. Civil Aircraft Design and Research, 1999(2): 11-19 (in Chinese).
[11] 杨超, 王立波, 谢长川, 等. 大变形飞机配平与飞行载荷分析方法[J]. 中国科学: 技术科学, 2012, 42(10): 1137-1147.
YANG C, WANG L B, XIE C C, et al. Aeroelastic trim and flight loads analysis of flexible aircraft with large deformations[J]. Scientia Sinica (Technologica), 2012, 42(10): 1137-1147 (in Chinese).
[12] CHEN P C, GAO X W, Tang L. An overset field-panel method for unsteady transonic aerodynamic influence coefficient matrix generation: AIAA-2004-1512[R]. Reston: AIAA, 2004.
[13] CHEN P C, GAO X W, TANG L. Overset field-panel method for unsteady transonic aerodynamic influence coefficient matrix generation[J]. AIAA Journal, 2004, 42(9): 1775-1787.
[14] 张淼, 刘铁军, 马涂亮, 等. 基于CFD方法的大型客机高速气动设计[J]. 航空学报, 2016, 37(1): 244-254.
ZHANG M, LIU T J, MA T L, et al. High speed aerodynamic design of large civil transporter based on CFD method[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(1): 244-254 (in Chinese).
[15] LIU D, KAO Y F, FUNG K Y. An efficient method for computing unsteady transonic aerodynamic of swept wings with control surface[J]. Journal of Aircraft, 1998, 25(1): 25-31.
[16] KRIST S L, BIEDRON T, RUMSEY C L. CFL3D user’s manual (Version 5.0): NASA/TM-1998-208444[R]. Washington, D.C.: NASA, 1998.
[17] LU S, VOSS R. TDLM—A transonic doublet lattice method for 3D potential unsteady transonic flow computation: DLR-FB 92-95[R]. Goettingen, FRG: DLR Institute fur Aeroelastik, 1992.
[18] STEIGINGA A, HOUWINK R. Correlation of experimental and quasi-3D theoretical airloads on the osillating LANN supercritical wing model: AFWAL-TR-83-3050[R]. Amsterdam: National Aerospace Lab, 1983.
[19] SMITH T A, HAKANSON J W, NAIR S S, et al. State-space model generation for flexible aircraft[J]. Journal of Aircraft, 2004, 41(6): 1473-1481.
[20] MOR M, LIVNE E. State-space unsteady aerodynamic for aeroservoelastic configuration shape optimization of flight vehicles: AIAA-2004-1762[R]. Reston: AIAA, 2004.
[21] SUH P M, CONYERS H J, MAVRIS D N. Rapid state space modeling tool for rectangular wing aeroservoelastic studies: AIAA-2015-1135[R]. Reston: AIAA, 2015.
[22] 杨超, 黄超, 吴志刚, 等. 气动伺服弹性研究的进展和挑战[J]. 航空学报, 2015, 36(4): 1011-1033.
YANG C, HUANG C, WU Z G, et al. Program and challenges for aeroservoelasticity research[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(4): 1011-1033 (in Chinese).
[23] 宋晨, 杨超, 吴志刚. 3种气动弹性状态空间建模方法的对比[J]. 航空学报, 2007, 28(S1): 82-86.
SONG C, YANG C, WU Z G. Comparison of three aeroelastic state space modeling methods[J]. Acta Aeronautica et Astronautica Sinica, 2007, 28(S1): 82-86 (in Chinese).
[24] BALDELLI D H, CHEN P C, PANZA J. Unified aeroelastic and flight dynamic formulation via rational function approximations [J]. Journal of Aircraft, 2006, 43(3): 763-772.
张辉男, 博士研究生。主要研究方向: 理论与计算流体力学, 气动弹性力学。
Tel.: 13991164363
E-mail: zhanghui_0104@126.com
李杰男, 博士, 教授, 博士生导师。主要研究方向: 理论与计算流体力学, 设计空气动力学。
Tel.: 13679258367
E-mail: lijieruihao@163.com
*Correspondingauthor.Tel.:13679258367E-mail:lijieruihao@163.com
Maneuverloadanalysisforflexibleaircraftintransonicflow
ZHANGHui,LIJie*
SchoolofAeronautics,NorthwesternPolytechnicalUniversity,Xi’an710072,China
Basedontheoversetfield-panelmethodforcomputingunsteadyaerodynamicsintransonicflows,thecalculationapproachofmaneuverloadforflexibleaircraftintransonicflowsisdeveloped,forthepurposeofprovidingexpedientandaccuratecriticalloadsforthedesigninstructuralstrengthofmodernaircraft.TheLANNwinginpitchmodeabout62%rootchordatMachnumber0.822issolvedtovalidatetheunsteadypressurecoefficientwiththeexperimentaldata,andexcellentagreementshowsthecapabilityoftheoversetfield-panelmethodinpredictingtheshocklocationandstrength.Statespacemodelforanalyzingmaneuverloadsisgeneratedthroughrationalaerodynamicapproximations,thenthetransientloadanalysisofatransportaircraftinpitchingisconductedtoinvestigatetheresponseoftheairframestatesandloadsactingonthecomponentsoftheaircraft.Theresultsindicatethatthepeakloadsactingonthewingandhorizontaltaildecreaseby5.1%and10.6%respectively,whileoneontheelevatorincreasesby16.2%,duetothestructuraldeformation.Therefore,theeffectofstructuraldeformationonloadsmustbeconsideredinthedesignconcerningstructuralstrengthofmodernaircraft.
maneuverload;unsteadyaerodynamics;aerodynamicinfluencecoefficientmatrix;transonic;ovesetfield-panelmethod
2015-12-28;Revised2016-01-31;Accepted2016-03-08;Publishedonline2016-03-171651
URL:www.cnki.net/KCMS/detail/11.1929.V.20160317.1651.008
s:NationalNaturalScienceFoundationofChina(11172240);AeronauticalScienceFoundationofChina(2014ZA53002);NationalBasicResearchProgramofChina(2015CB755800)
2015-12-28;退修日期2016-01-31;录用日期2016-03-08; < class="emphasis_bold">网络出版时间
时间:2016-03-171651
www.cnki.net/KCMS/detail/11.1929.V.20160317.1651.008
国家自然科学基金 (11172240); 航空科学基金 (2014ZA53002); 国家“973”计划 (2015CB755800)
*
.Tel.:13679258367E-maillijieruihao@163.com
张辉, 李杰. 弹性飞机跨声速机动载荷计算方法J. 航空学报,2016,37(11):3236-3248.ZHANGH,LiJ.ManeuverloadanalysisforflexibleaircraftintransonicflowJ.ActaAeronauticaetAstronauticaSinica,2016,37(11):3236-3248.
http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn
10.7527/S1000-6893.2016.0070
V 211.47
A
1000-6893(2016)11-3236-13

