Kriging模型及代理优化算法研究进展

韩忠华

西北工业大学 航空学院 翼型叶栅空气动力学国家级重点实验室， 西安 710072

Kriging模型及代理优化算法研究进展

韩忠华*

西北工业大学 航空学院 翼型叶栅空气动力学国家级重点实验室， 西安 710072

代理模型方法由于能显著提高工程优化设计问题的效率，在航空航天及其他领域得到了广泛重视，并逐渐发展成为一类优化算法，本文称其为代理优化(SBO)算法。在现有的代理模型方法中，如多项式响应面、径向基函数、神经网络、支持向量回归、多变量插值/回归、多项式混沌展开等，源于地质统计学的Kriging模型具有代表性，是一种非常具有应用潜力的代理模型方法。以飞行器设计领域的优化问题为背景，介绍了Kriging代理模型及应用于优化设计的理论和算法的最新研究进展。首先，概述了Kriging模型的基本理论和算法，并讨论了影响Kriging模型鲁棒性和效率的几个关键性问题。其次，回顾了Kriging模型理论和算法研究的3个最新研究进展，包括梯度增强型Kriging、CoKriging和分层Kriging模型。而后，分析提炼了基于Kriging模型的代理优化算法的优化机制和优化框架，给出了“优化加点准则”和“子优化”的概念，并介绍了目前常用的几种优化加点准则及其相应子优化问题的求解与约束处理；同时，还介绍了最新提出的局部EI加点准则以及代理优化的终止条件。最后，介绍了代理优化在标准测试函数算例验证、飞行器气动与多学科优化设计典型算例确认方面的研究进展，并对当前存在的一些关键科学问题以及未来研究方向进行了讨论。

优化方法； Kriging； 代理模型； 飞行器设计； 多学科设计优化(MDO)

现代优化方法在飞行器设计中的应用可追溯到20世纪50年代末60年代初，最初应用于结构优化设计[1-2]。大约20世纪70年代开始被引入到气动优化设计[3-4]，而后随着多学科设计优化(MDO)在20世纪80年代的兴起[5-6]，逐渐成为航空航天各学科领域的研究热点[7-8]。对于MDO的研究，由于涉及多个学科的大量设计变量和状态变量，且各学科之间可能存在复杂耦合关系，使得直接调用各学科高可信度分析模型(如计算流体力学(CFD)或计算固体力学(CSM))时，面临优化难度大、优化时间过长的问题。于是，代理模型方法应运而生，并逐渐得到重视，成为MDO研究的重要分支和关键技术[9-12]。

所谓代理模型，通常是指在分析和优化设计过程中可替代那些比较复杂和费时的数值分析的近似数学模型，也称为响应面模型、近似模型或元模型[13-15]。代理模型方法不仅可大大提高优化设计效率，而且可降低优化难度，并有利于滤除数值噪声和实现并行优化设计。代理模型方法的雏形是20世纪70年代应用于结构优化设计的多项式响应面[16-17]；自20世纪80年代MDO兴起后，代理模型方法成为了MDO研究的重要分支[18]；大约在20世纪末，代理模型方法被引入到气动优化设计领域[19-21]。在代理模型方法研究方面，目前已发展了包括多项式响应面 (RSM)[16-17]，Kriging模型[22-23]、径向基函数(RBFs)[24-27]、神经网络(NN)[28-29]、支持向量回归 (SVR)[30-31]、多变量插值和回归 (MIR)[32-33]、多项式混沌展开(PCE)[34-35]等多种代理模型方法[31，36-38]。文献[31，36]对代理模型方法及其应用的发展进行了回顾。在多维空间样本点合理选取研究方面，除了采用经典试验设计方法外(例如全因子、中心组合、D-优化等)，目前还发展了适用于计算机数值模拟实验的拉丁超立方 (LHS)[39]、正交设计、均匀设计 (UD)[40]等现代试验设计方法。

在代理模型方法发展之初，其作用是作为近似模型，用于替代比较复杂和费时的数值分析模型进行优化设计。对于这种“替代算法”，优化结果很大程度上依赖于代理模型近似精度，且无法保证能收敛到真实最优解。近年来，随着研究的不断深入，代理模型的作用发生了转变，不再是简单替代，而是构成了一种基于历史数据来驱动样本点加入，并逼近局部或全局最优解的优化机制。在这种新的优化机制下，通过合理构造加点策略，可保证所产生的样本点序列精确收敛于优化问题的真实最优解。同时，复杂多维问题的代理模型不必在整个设计空间内具有高的近似精度，而只需在重要的区域特别是最优解附近具有高的近似精度。总之，由于代理模型在优化设计问题中作用的转变(以及一系列特定算法的产生)，使得基于代理模型的优化方法正逐渐发展成为可与传统梯度优化和无梯度优化具有相同功能的一类通用优化方法[38]。为了方便起见，本文称其为代理优化(Surrogate-based Optimization， SBO)算法。

在现有的代理模型方法之中，源于地质统计学的Kriging模型是一种具有代表性的方法。Kriging模型(也称为高斯随机过程模型或克里金模型)的思想由南非采矿工程师Krige于1951年在其硕士论文中提出[22](Krige的生平可参见文献[31])。在1963—1971年期间，法国数学家Matheron进行了完善和发展，形成了完整的数学理论和模型[41](称为区域变量理论[42])。出于对Krige教授开创性工作的尊重，他在1963年首次将该理论称为Krigeage[41](后来人们称其为Kriging模型)。

Kriging模型理论形成后，最初应用于地质储量估计，后来发展成为一类非常流行的地质统计学插值方法。1989年，Sacks 教授等[23]将Kriging理论进一步推广到确定性计算机实验的设计和分析领域，并给出了一种较实用的Kriging算法(或Kriging模型)。由于Sacks 教授等里程碑式的研究工作，使得 Kriging模型不仅在地质、水文、气象、环境科学等自然科学领域得到应用，也在航空航天、汽车等工程科学领域得到研究、发展和应用。Kriging模型不仅能给出对未知函数的预估值，还能给出预估值的误差估计，这是Kriging模型区别于其他代理模型的显著特点。Kriging模型由于其对非线性函数的良好近似能力和独特的误差估计功能，正受到越来越多研究者的关注，是目前最具代表性和最具应用潜力的代理模型方法之一。

在飞行器设计领域，随着各学科高可信度数值模拟技术(如CFD或CSM)的发展和现代优化算法的应用，Kriging模型已经逐步引起了该领域科研人员和工程设计人员的重视[43-45]。基于Kriging模型的代理优化算法，被尝试应用于气动优化设计[46-52]、结构优化设计[53-54]、导弹设计[55-56]、航天飞行器设计[57]、高速列车外形优化设计[58]以及多学科优化设计[59-60]，并很可能发展成为该领域最实用和最流行的优化方法。但是，与经典的梯度优化算法[61]和进化算法(如遗传算法[62]) 等优化算法相比，基于Kriging模型的代理优化算法虽然潜力巨大，但由于发展时间较短，有些算法还不够成熟。目前所发表的关于Kriging模型的文献分散在众多不同学科领域，采用不同行业的科学语言进行表述，缺乏系统性和通用性。特别在该航空航天领域，目前还没有专门介绍Kriging模型理论、算法以及最新研究进展的综述性文献报道，可供研究人员参考的经验也很少。

在航空航天领域，由于各学科数值模拟技术的日益成熟，基于高可信度数值模拟技术的优化设计方法及其在飞行器设计中的应用，将继续成为未来10～20年内的研究热点之一。例如最近NASA发布的2030年CFD愿景研究报告中[63]，多学科分析与优化被列为需要重点发展的6大关键领域之一。因此，研究更高效、更实用的代理模型及其相应的优化理论和算法，无疑将是一项重要内容。

本文以飞行器设计领域的优化问题为背景，系统介绍Kriging模型及其优化设计方法的最新进展。第1节概述了Kriging模型基本理论和算法；第2节对Kriging模型理论和算法研究的最新进展进行了综述，并讨论了影响建立Kriging模型的鲁棒性和效率的几个关键性问题；第3节介绍了将Kriging模型应用于优化设计问题的代理优化算法最新进展，包括优化加点准则和最新约束处理方法；第4节给出了代理优化算法验证与确认的最新进展；最后，对该领域存在的若干关键科学问题及未来发展方向进行了讨论。

1 Kriging模型基本理论和算法概述

Kriging模型存在不同变种，根据其采用的全局趋势模型不同，可分为“简单Kriging”、“普通Kriging”和“泛Kriging”。这里以最常用的普通Kriging为例，对Kriging模型的基本理论和算法进行简要介绍。

1.1 代理模型问题的基本描述

应用于飞行器优化设计的数值分析方法(如CFD或CSM)，其共同特点是采用迭代方法求解所满足的控制方程，最终获得所关心的性能数据，如升力、阻力和力矩或应力、变形等。对优化设计问题而言，可将数值分析程序或软件看成一个“输入-输出”系统，即作为输出量的目标函数和约束函数可看成是设计变量的函数。如果能建立目标函数和约束函数对设计变量的代理模型，就能对最优点进行快速预测，从而大大提高优化效率。

(1)

对这n个设计方案进行数值分析(CFD或CSM)，从分析结果中得到相应的n个函数响应值：

yS=[y(1)y(2)…y(n)]T=

(2)

1.2 Kriging模型及其预估值

Kriging模型是一种插值模型，其插值结果定义为已知样本函数响应值的线性加权，即

(3)

于是，只要能给出加权系数ω=[w(1)w(2)…w(n)]T的表达式，便可得到设计空间中任意设计方案的性能预估值。为了计算加权系数，Kriging模型引入统计学假设：将未知函数看成是某个高斯静态随机过程的具体实现。该静态随机过程定义为

Y(x)=β0+Z(x)

(4)

式中：β0为未知常数，也称为全局趋势模型，代表Y(x)的数学期望值；Z(·)为均值为零、方差为σ2(σ2(x)≡σ2,∀x)的静态随机过程。在设计空间不同位置处，这些随机变量存在一定的相关性(或协方差)。该协方差可表述为

Cov[Z(x),Z(x′)]=σ2R(x,x′)

(5)

式中：R(x,x′)为 “相关函数”(只与空间距离有关)，并满足距离为零时等于1；距离无穷大时等于0；相关性随着距离的增大而减小。

基于上述假设，Kriging模型寻找最优加权系数ω，使得均方差

(6)

最小，并满足如下插值条件(或无偏差条件)：

(7)

采用拉格朗日乘数法，经过推导可证明最优加权系数ω由式(8)描述的线性方程组(也称为Kriging模型方程组)给出

(8)

式中：i=1,2，…，n；μ为拉格朗日乘数。式(8)写成矩阵形式为

(9)

式中：

(10)

其中：R为“相关矩阵”，由所有已知样本点之间的相关函数值组成；r为“相关矢量”，由未知点与所有已知样本点之间的相关函数值组成。求解线性方程组式(9)，并代入式(3)可得Kriging模型预估值为

(11)

通过分块矩阵求逆，该模型可最终写为

(12)

式中：β0=(FTR-1F)-1FTR-1yS；列向量Vkrig只与已知样本点有关，可在模型训练(见1.4节)结束后一次性计算并存储。之后，预测任意x处的函数值只需要计算r(x)与Vkrig之间的点乘，其计算时间相比CFD或CSM分析而言完全可以忽略。此外，Kriging模型还能够给出预估值的均方差估计：

σ2{1.0-rTR-1r+(1-FTR-1r)2/FTR-1F}

(13)

该均方差可用于指导加入新样本点，以提高代理模型精度或逼近优化问题的最优解(见第4节)。

1.3 相关函数的选择

在式(12) 所示的Kriging模型中，R和r的构造均涉及相关函数的选择和计算。目前比较流行的一类相关函数为

(14)

1≤pk≤2；k=1,2，…,m

(15)

图1 一维高斯指数函数示意图Fig.1 Schematic of 1D Gaussian exponential function

实践证明，在实际应用中一些其他的相关函数可近似满足高斯假设，也具有很好的性能。例如，目前比较流行一类三次样条函数：

(16)

该函数二阶可导，在光滑性和鲁棒性方面取得很好的折中。

1.4 模型参数训练(或优化)

建立Kriging模型时，可以对其模型参数(或超参数)进行训练，从而大大增强代理模型的灵活性。一般采用“最大似然估计”或“交叉验证”[66]。最大似然估计是使式(17)函数值最大：

(17)

式中：超参数p仅针对高斯指数函数才存在；|R|为相关矩阵的行列式。对于式(17),β0和σ2的最优值可解析地给出：

β0(θ,p)=(FTR-1F)-1FTR-1yS

(18)

将式(18)代入式(17)后，取对数，并忽略常数项，优化问题转化为使式(19)最大：

(19)

由于无法解析地求出θ和p的最优值，这里需要采用数值优化算法，如拟牛顿方法等梯度优化算法[61]或Hooke & Jeeves模式搜索[67]、Simplex单纯形法[68]、遗传算法[62]等无梯度算法。文献[45]深入讨论了Kriging模型超参数训练方法。

1.5 Kriging模型具体实现的几个关键性问题

采用上述理论编写一个可用的Kriging模型计算机程序并非难事,例如较早流行的DACE工具箱[69]就是用MATLAB编写，语句较少。但是，不同 Kriging模型程序的性能却差异很大。根据作者多年成功开发Kriging模型程序的经验，这里介绍影响Kriging模型的效率和鲁棒性的几个关键问题，供读者参考。

首先，需要对样本点进行归一化。所谓归一化，也就是将样本点各设计变量的取值均转化到 某个统一的区间(例如[0,1]或[-1,1])上：

(20)

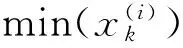
其次，必须合理地进行模型参数的优化。合理的模型参数，可显著提高Kriging模型近似精度，使之明显优于多项式响应面、径向基函数等代理模型。但是，不恰当的模型参数值，可能使Kriging模型预测精度差，甚至建立失败。

再次，需要在任何情况下保证Kriging模型相关矩阵R的正定性。在某些极限情况下，例如两个样本点无限靠近时，相关矩阵的两行或两列近似相等，出现奇异性。即便不出现上述极限情况，矩阵的条件数可能很大，使得求解Kriging线性方程组的误差较大，导致模型预测精度降低甚至预测失败。为了增加鲁棒性，可采用所谓的“正则化”方法(或加入所谓的Nugget效应[70])，在矩阵R对角线上加一个小的常数：

R′=R+γI

(21)

γ=(103+n)εM

(22)

其中：εM=2.22×10-16为双精度时的机器零(不同的计算机可能不同，读者可以自己测试)。另外，γ取值越大，Kriging模型越趋近于回归模型, 从而可滤出数值噪声[71]。

最后，需要采用合理的矩阵分解方法。就建立Kriging模型本身的计算量而言，最耗时部分是相关矩阵求逆。为了提高效率，一般不需要直接求逆，而是求出R-1与矢量的乘积(如R-1yS或R-1r)即可。一种比较有效的方法是采用LU(Lower-upper)分解；但由于相关矩阵对称正定，因此可采用效率更高的Cholesky分解：

R=LLT

(23)

(24)

式中：i,j=1,2,…,n。

理论分析和实践表明，Cholesky分解的效率比LU分解提高1倍。对于具有n个样本点的问题，Cholesky分解的浮点计算次数(FLOPS)和内存占用量约为

FLOPS≈(1/3)n3+2n2

Memory size≈8×10-6n2MB

(25)

2 Kriging模型理论和算法研究新进展

经过调研，认为Kriging模型理论和算法的发展及其在航空航天工程设计领域的应用共经历了4个阶段：① 20世纪50年代初至70年代初，是Kriging模型思想的提出和理论形成阶段[22，41-42]；② 20世纪70年代初至80年代后期，是Kriging模型理论和算法的发展和成熟阶段[23]；③ 20世纪90年代初至20世纪末，是Kriging模型在航空航天领域初步应用的阶段[72-78]；特别是随着MDO研究的兴起，代理模型技术得到高度重视，Kriging模型成为最具代表性的代理模型之一；④ 21世纪是Kriging模型理论和算法的进一步完善[43-45,71,79]，并在航空航天领域进一步应用的阶段[80-81]。

这里结合本文的研究工作，重点介绍21世纪以来，在Kriging模型的研究和应用过程中，出现的具有代表性的3个研究新进展。

2.1 梯度增强型Kriging模型

梯度信息可用于提高Kriging模型精度[82-85]。而如果采用Adjoint方法[86]等快速求解梯度方法，还可提高建立Kriging模型的效率[87-88]。与传统有限差分法相比，Adjoint方法的优点在于只需求解一次流动控制方程和伴随方程[86]，便可获得对所有设计变量的梯度，梯度计算效率与设计变量数无关。利用梯度信息来提高Kriging模型的精度，成为一种新的代理模型方法，称为梯度增强型Kriging (Gradient-Enhanced Kriging, GEK)模型

实现引入梯度信息的最简单做法是利用一阶泰勒展开：

(26)

式中：i=1,2，…,n；k=1,2，…,m。

将某样本点处的m个偏导数值变成m个附加样本点的函数值，然后再基于这n+n×m个样本点建立Kriging模型。该方法缺点是：其近似精度与步长Δxk密切相关；步长太大，数值误差较大；步长太小，容易出现相关矩阵的奇异性。该方法是一种间接引入梯度信息方法[84]。

这里介绍一种直接引入梯度信息的方法。需要说明的是，除了一阶导数信息外，二阶导数信息(Hessian)也可用于提高代理模型的精度[89]。由于获得二阶导数的计算代价较大，且对于提高代理模型精度的作用有限，因而下文中主要介绍如何在Kriging模型中引入一阶偏导数信息。

对于一个具有m个设计变量的优化问题，首先假设对目标函数(或状态变量)y在n个抽样位置，获得n个函数值及n×m个偏导数值。则式(1)和式(2)中的抽样位置及函数响应值相应地变为

S=[x(1)…x(n)x(1)…x(1)…

(27)

由式(27)可知，每一个偏导数信息都被看作是一个独立的样本信息。这种表述方法具有一般性：如果在某些样本点处梯度信息不可用，便从上述样本数据集的相应位置上去除即可；如果没有任何偏导数信息，GEK模型将退化为传统的Kriging模型。因此，GEK模型是一种可考虑梯度信息的更一般化的Kriging模型。

GEK模型对未知函数的预估值定义为所有抽样函数值和偏导数值的线性加权，即

(28)

Cov[Z(x(i)),Z(x(j))]=σ2R(x(i),x(j))

(29)

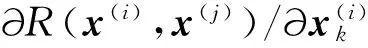
与传统的Kriging模型类似，可推导出GEK模型对未知函数的预估值表达式为

(30)

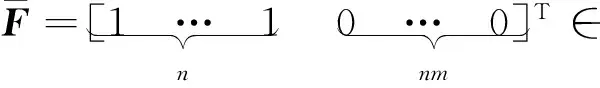
(31)

(32)

其中：相关矩阵R、一阶导数矩阵∂R以及二阶导数矩阵∂2R定义为

(33)

相关矢量r及其一阶导数∂r定义为

(34)

GEK模型对预估值的均方差估计为

(35)

在构造GEK模型过程中，模型参数训练方法见文献[88，90]。

需要说明的是，GEK模型相关矩阵中还涉及相关函数的一阶和二阶导数。对于三次样条函数，可推导出其一阶导数为

(36)

(37)

且Rk和ξl的计算参见式(16);sign()为取符号运算。

同理，可推导出其二阶导数表达式为

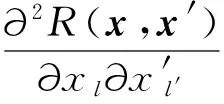
(38)

(39)

2.2 CoKriging模型

CoKriging模型是20世纪70年代发展起来的一种更有效的地质统计学插值模型[91-95]。在地质统计学领域，为了提高对某个抽样比较困难的量的预测精度，提出了采用更容易抽样的量进行辅助预测的Kriging模型，称为CoKriging模型[92]。2000年，Kennedy和O’Hagan[96]首次将CoKriging模型推广应用于工程科学领域，发展了一种采用低可信度计算机程序结果，来辅助预测高可信度计算机程序结果的CoKriging方法。目前国际上对CoKriging模型的研究主要集中在地质统计学和数学统计学等领域，在航空航天等工程科学领域的研究也逐渐得到重视[14，97-101]。

2010年，文献[101]独立提出了一种可用于建立变可信度代理模型的实用CoKriging模型(见文献[14])。下面对该模型进行介绍。

对于一个具有m个设计变量的优化问题，在设计空间中同时采用高可信度分析(例如Navier-Stokes方程或密网格数值模拟)和低可信度分析(例如Euler方程或疏网格数值模拟)进行抽样，并建立所谓的变可信度代理模型。更多建立变可信度模型的方法请参见文献[88]。变可信度代理模型在达到相同近似精度的条件下，可显著提高建立代理模型的效率。

假设高、低可信度分析程序的抽样位置为

(40)

式中：下标“1”和“2”分别代表高、低可信度，例如n1和n2分别代表高、低可信度样本点数(假设n2≫n1)。相应的目标函数或约束函数的响应值为

(41)

CoKriging模型预估值定义为

(42)

式中：λ1、λ2分别为对高、低可信度响应值的加权系数。假设存在分别与y1、y2对应的2个静态随机过程：

(43)

则设计空间不同位置处，随机变量之间的协方差和交叉协方差定义为

(44)

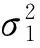
(45)

(46)

且有

(47)

Cokriging模型预估值的均方差为

(FTR-1F)-1(φ-FTR-1r)

(48)

(49)

剩余参数θ(11)、θ(12)、θ(22)没有解析最优解，可以通过数值优化方法求解式(50)的最大值得到

(50)

需要说明的，上述CoKriging模型也可引入梯度信息，得到梯度增强CoKriging模型(GECK，见文献[101]附录部分)。

由于可合理假定高、低可信度数值分析结果具有相似的函数变化趋势，为简化起见，可假定

(51)

式中：h为空间距离；ρ为避免出现矩阵奇异接近1的常数，可取ρ=0.999 9。

2.3 分层 Kriging 模型

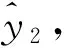
首先，假设y1对应的随机过程定义为

(52)

式中：β0为待定的自适应因子，它反映了高、低可信度函数之间的相关性；如果β0=0，说明高、低可信度函数之间没有相关性。β0的引入，有效避免了引入低可信度分析后代理模型精度反而变差的风险。采用与Kriging模型类似的推导方法(详细推导过程见文献[13])，可得到HK模型的预估值为

(53)

式中：

(54)

预估值的均方差为

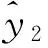
(55)

HK 模型的参数训练方法与第1节中Kriging模型基本相同，这里不再赘述。需要说明的是，如果存在梯度信息，可采用2.1节类似的方式引入梯度信息，形成梯度增强型分层Kriging模型。

2.4 有关Kriging模型的其他研究新进展

限于篇幅，这里简要介绍关于Kriging模型的其他代表性研究进展。文献[71]采用最大似然估计对式(21)的正则化参数γ进行优化，发展了可滤除数值噪声的Kriging模型。此外，传统 Kriging模型采用预设的全局趋势模型,这样的近似精度可能不是最佳的。于是，文献[102]发展了一种采用贝叶斯理论框架来识别其趋势模型的方法，称为“盲Kriging”模型。为了避免识别过程陷入局部最优，文献[103-104]分别采用遗传算法和交叉验证来寻找Kriging模型最优趋势模型，发展了所谓的“动态Kriging”模型。针对传统Kriging模型无法处理具有随机性的计算机实验的问题，文献[105]引入固有不确定性(Intrinsic Uncertainty) 和非固有不确定性(Extrinsic Uncertainty)的概念，并提出了1种所谓的“随机Kriging模型”，可用于鲁棒优化设计问题。

3 基于Kriging模型的代理优化算法

第1节和第2节中介绍了如何建立Kriging代理模型。本节讨论将其应用于求解式(56)一般性优化问题的研究新进展：

Miny(x)

(56)

式中：y(x)、gi(x)为目标函数与约束函数；NC为约束个数；xu、xl为设计变量的上、下限。

本节首先通过与传统优化算法比较，梳理提炼出了代理优化算法的优化机制和算法框架。其次，给出了“优化加点准则”和“子优化”的概念，并针对常用优化加点准则，介绍了特定的约束处理和混合子优化技术；同时，还介绍了1种改进的加点准则。最后，给出了优化终止条件。

3.1 代理优化算法框架

将代理模型用于求解优化设计问题，最初采用的方法是在建立具有合理精度的代理模型后，采用代理模型去替代比较费时的精确数值模拟分析，进行优化设计。很显然，这种替代算法很大程度上依赖于代理模型精度；如果精度过低，将可能导致优化效果不佳甚至失败。这种方法也被称为第1代方法。第1代方法尽管被人们广为接受，但由于没有形成独立的优化机制，因而无需讨论其算法框架。后来，人们发展了根据一定的准则加入新的样本点，循环更新代理模型的第2代方法，并逐步发展成为今天的代理优化算法。但直到目前，国际上还没有讨论代理优化算法的通用算法框架的文献报道。

于是，在文献调研和研究实践基础上，本文对传统优化方法和代理优化方法[15]的算法框架进行了比较(图2和图3)。不难看出，代理优化算法的基本原理和过程可描述为：① 对设计空间进行试验设计抽样并运行精确数值模拟分析获得响应值，建立初始代理模型；② 基于代理模型，按照一定的优化加点准则(如最小化代理模型预测(MSP)、改善期望(EI)、改善概率(PI)、均方差(MSE)、置信下界(LCB)等)，采用传统优化算法求解相应的子优化问题，以很小的计算代价，对最优解进行预测；③ 对这些预测的最优解再次运行精确数值分析，并将结果作为新的样本数据添加到现有数据集中，不断更新代理模型，直到所产生的样本点序列收敛于局部或全局最优解。

图2 传统的梯度或无梯度优化框架Fig.2 Framework of conventional gradient-based and gradient-free optimizations

图3 代理优化算法框架Fig.3 Framework of SBO algorithm

图4 按通用优化算法重新整理的代理优化算法框架Fig.4 Rearranged framework of SBO algorithm using general optimization algorithm

为了更好地认识代理优化算法，对图3进行重新整理，将“建立代理模型和根据加点准则的子优化”过程看作一个独立模块，得到图4。比较图4 和图2，不难发现，除优化器(Optimizer)模块外，二者完全相同。这就是说，“建立代理模型和根据加点准则的子优化”是代理优化算法的优化机制。

从代理优化算法的原理不难看出，初始样本的选择、代理模型及其训练、优化加点准则及其子优化求解，是代理优化算法的3大要素。

3.2 试验设计与初始样本选择

代理优化算法的第1步是选择初始样本点，并建立初始代理模型。虽然理论上可以像梯度优化算法那样只给出1个初始点，但针对全局优化问题，更好的方法是通过试验设计(DoE)选取1组样本。

试验设计的思想是通过选取最少的样本点，使获取的关于未知设计空间的信息最大化。Giunta等在文献[39]中将DoE方法分为两类：经典试验设计和现代试验设计方法。经典试验设计方法包括全因子设计、中心组合设计(CCD)、Box-behnken设计、D优化(D-Optimal)方法等。经典试验设计方法主要用于安排仪器实验,并考虑到如何减小实验随机误差的影响。现代试验设计方法包括拟蒙特卡罗方法、准蒙特卡罗方法、拉丁超立方、正交试验设计(OAD)、哈默斯利序列采样方法(HSS)。中国方开泰教授发明的均匀设计[40]也属于现代试验设计方法的范畴。现代试验设计主要采用“空间填充”的思想，用于安排确定性的计算机试验，其中尤以拉丁超立方和均匀设计方法比较流行。图5给出了针对2个变量(V1和V2)选取25个样本点的示意图。

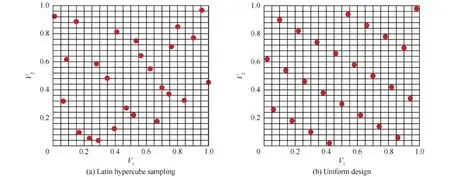
图5 采用拉丁超立方和均匀设计针对2维设计空间选择的25个样本点示意图Fig.5 Schematics of 25 sample points selected by Latin hypercube sampling and uniform design for a 2D design space

不同试验设计方法选取的样本点不同，导致初始代理模型的近似精度不同，从而对代理优化的效率有影响。同样影响优化效率的是初始样本点数目。文献[31，37]讨论了样本点数的选择。对于传统代理模型优化方法，必须使代理模型具有足够精度。因而一般初始样本点数与后期增加的样本点数的比值在2∶1以上。例如对于二次响应面方法，对于m维问题的初始样本点数必须大于m(m+1)/2。而对于基于Kriging模型的代理优化算法，初始样本点数理论上不受设计空间维数的限制，且优化效率对初始样本点数的依赖也并不明显。一般情况下初始样本点数与后期增加的样本点数之比在1∶2 以下。

3.3 优化加点准则及其子优化求解

建立初始代理模型后，下一步是通过一定的法则循环选择新的样本点，直到优化收敛。所谓“优化加点准则”[15,31,71,106]，是指如何由所建立代理模型去产生新的样本点的法则或规则。所谓“子优化”，是相对主优化而言，指采用传统优化算法求解由加点准则所确定的优化问题，得到新的样本点的过程。主优化加点循环中的每一步，都要进行一次完整的子优化迭代，直到子优化收敛。但由于在子优化中，无需访问精确数值分析，因此计算时间可以忽略。

针对基于Kriging模型的代理优化算法，国际上已经发展了多种加点准则[31,106-107]，包括MSP准则[15，108]、EI准则[15，20，74]、PI准则[106-107，109]、MSE准则[106，109]、LCB准则[75，106-107]。为了说明这5种常见加点准则的原理和子优化问题的建立，下面以某一维函数为例，采用4个样本点S=[0 0.4 0.6 1.0]T建立Kriging模型。该一维函数来自文献[31]，表达式为

y=(6x-2)2sin(12x-4)x∈[0,1]

(57)

3.3.1 最小化代理模型预测准则

最小化代理模型预测准则是最简单、最直接，也是最早被采用的方法[15，106-110]。其原理是直接在代理模型上寻找目标函数的最小值。带约束的子优化问题数学模型为

(58)

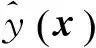
图6 一维问题MSP加点法则原理图Fig.6 Schematic of MSP infill-sampling criterion for a 1D problem

对于全局优化问题，为了提高子优化的精度，本文作者最近提出了一种遗传算法与梯度优化算法相结合的混合子优化方法。将多种优化算法获得的目标函数值最小的解作为式(58)子优化的最终优化解。对于遗传算法，可采用文献[111]提出的约束处理方法。在该方法中，遗传算法的适应度函数值为

(59)

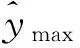
对于局部优化问题，可采用当前最优点作为初始点，直接采用BFGS、SQP等梯度优化算法[61]或Hooke & Jeeves[67]、Simplex[68]等局部搜索算法进行子优化。另外，为了确保代理优化算法收敛性，文献[38，112]还给出了一种信赖域方法。即在初始点附近设定一个初始的信赖域半径r0，建立代理模型后，子优化只在信赖域内进行，即搜索范围限制为

x∈[max(x0-r0,xl),min(x0+r0,xu)]

(60)

式中：x0为优化初始点(或样本点中满足约束的最优点)。对子优化结果，采用精确数值模拟分析并更新代理模型，同时调整信赖域半径大小，直到整个优化收敛。文献[38，112]给出的信赖域半径调整方法为

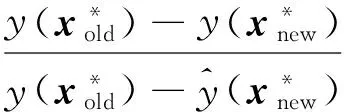
(61)

式中：质量因子δ′为目标函数的实际改善与预测改善的比值。δ′的合理计算是其中的关键；如果计算不合理，可能使信赖域半径缩小过快，从而导致优化出现早熟。因此，还有待于发展更好的质量因子计算方法或其他提高收敛性的方法。

3.3.2 改善期望准则

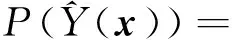
(62)

对于最小化问题，目标函数改善量I(x)定义为

(63)

I(x)的期望值为[15,74,107]

E[I(x)]=

(64)

图7 某一维问题EI函数分布示意图 Fig.7 Schematic of EI function distribution for a 1D problem

通过求解最大化EI值的子优化问题：

MaxE[I(x)]

s.t.xl≤x≤xu

(65)

从而可得到新的样本点x*。

(66)

这样可以得到所谓的约束EI值为[109-110]

Ec[I(x)]=E[I(x)∩Gi≤0]=

(67)

于是，可采用3.3.1节中提出的混合子优化方法，求解无约束子优化问题：

s.t.xl≤x≤xu

(68)

从而得到新的样本点x*。

EI 方法理论上是一种全局优化算法[74，107]，但优化后期收敛较慢。于是，本文作者最近提出了一种所谓的“局部EI”方法。其基本思想是：优化过程中，代理优化的子优化不必找到整个设计空间内EI函数的最大值，而只需在当前最优点附近寻找一个较大的值即可。这种方法是受到梯度优化算法的启发。众所周知，梯度优化过程中每一步的线搜索过程不一定要精确进行，只需搜索有限步数即可(满足所谓的“Armijo准则”)。因而不难想到, 对于EI最大值搜索也不需要精确进行，而是在一定范围内搜索即可。实践证明，这样不仅能显著提高收敛效率，而且能保持一定的全局优化性能，对于实际的工程设计问题可能是一种比较好的选择。

3.3.3 改善概率准则

改善概率准则方法[31]实际上是EI方法派生的方法。与EI准则类似，该准则通过计算目标函数改善的概率，并将改善概率最大点作为新的样本点。目标函数改善的概率为[106-107，109]

(69)

对于上述一维问题，PI函数分布如图8所示。

图8 某一维问题的PI函数分布示意图 Fig.8 Schematic of PI function distribution for a 1D problem

对于约束优化问题，可采用与约束EI类似的方法进行处理。于是，可采用3.3.1节提出的混合子优化方法，求解下面的子优化问题

s.t.xl≤x≤xu

(70)

得到新的样本点x*。

3.3.4 均方差准则

均方差准则(MSE)方法是直接运用Kriging模型提供的均方差估计(或均方根误差(RMSE),如图 9所示)的一种改善代理模型全局精度的加点准则。即采用遗传算法等全局优化算法，并结合局部优化算法，求解下面的子优化问题[106，109]：

s.t.xl≤x≤xu

(71)

从而得到新样本点x*。对于带约束的问题，可引入满足约束的概率，可求解下面的子优化问题

s.t.xl≤x≤xu

(72)

得到新的样本点x*。

图9 某一维问题的均方根误差函数分布示意图Fig.9 Schematic of RMSE function distribution for a 1D problem

3.3.5 置信下界准则

(73)

图10 某一维问题的LCB函数分布示意图Fig.10 Schematic of LCB function distribution for a 1D problem

该准则约束的处理与MSP准则类似。即可采用3.3.1节提出的混合子优化方法求解下面的约束子优化问题

(74)

从而得到新的样本点x*。

文献[106-107，113]均对上述优化加点准则进行了比较，得到了一些具有指导性的建议。这里再补充几点说明：

1) 除MSP准则适用于多项式响应面、径向基函数等其他代理模型外，EI、PI、MSE、LCB准则一般只适用于Kriging模型以及其他具有误差估计功能的代理模型。

2) 除上述的5种比较流行的加点准则，还可采用目标搜索(Goal-seeking)[107]和条件下界等方法[31]。但这些准则不是通用的加点准则。

3) 各种加点准则可组合使用，形成组合加点法则。组合加点不仅可克服单一准则的缺陷，提高其鲁棒性。另外，还可在每一步迭代加入任意点数的新样本点，这就是所谓的多点加点法则[114]或并行加点法则[31]。

4) 不仅可用于单目标优化，也可用于多目标优化[20，31]。

5) 既可用于全局优化，也可用于局部优化问题。对于局部优化问题，为了提高收敛性，可采用信赖域方法[107]和采用梯度增强型Kriging[113]。

3.4 代理优化的终止条件

优化终止条件是优化算法必须要具备的一个因素。目前国内外还没有关于定义代理优化算法优化终止条件的文献报道。于是，本文作者最近根据代理优化的特点，并借鉴其他优化算法的终止条件，定义了如下4种终止条件。

首先，可以根据样本点之间的距离和目标函数值的差别进行定义：

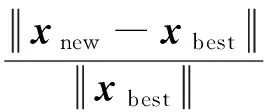
(75)

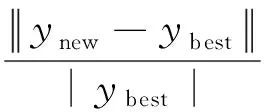
(76)

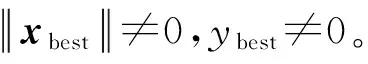
其次,可根据代理模型在最优点附近的近似精度来定义：

(77)

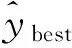
再次，可根据计算资源情况，设定调用精确数值模拟分析的最大次数：

N≤Nmax

(78)

例如针对气动优化设计问题，由于计算资源有限，一般希望在100～300次CFD计算以内，获得最优的外形，因此可以设定Nmax=100～300。

最后，可针对特定的加点准则进行定义。例如针对EI准则，可定义为

max(EI)≤EImin

(79)

也就是说当子优化求解得到的最大EI值小于某一个阀值时，优化即可终止。例如，在气动减阻优化中，可设定EImin=1.0×10-6，也就是说如果最大EI值小于0.01 counts时，优化即可终止。

4 基于Kriging模型的代理优化算法验证和确认

代理模型最初作为一种近似方法，用于提高采用高可信度数值分析的工程设计问题的效率[76]。因此，人们往往针对特定的问题发展特定的代理优化框架，例如文献[20-21]中发展的翼型优化设计方法，文献[52，85]的机翼优化设计方法，以及文献[54]发展的结构优化设计方法。但是，代理优化算法如果作为一种通用的优化算法框架，就需要经过优化标准算例的验证和确认，以评估算法的效率和精度，并对算法进行相应的改进。对于代理优化算法的效率，一般通过目标函数计算次数来评估[107]；因为在实际工程设计问题中，调用高可信度数值模拟来计算目标函数往往是整个优化流程中最费时的部分。目前，关于代理优化算法的验证和确认的研究工作开展得比较少。

4.1 标准测试函数优化算例验证

Jones等在1998年提出著名的EI方法时，只采用了4种比较简单的测试函数算例进行验证[74，107]，包括2维Branin-Hoo函数、Goldstein-Price函数、3维和6维Hartman函数，且这些都是无约束问题。Sasena[109]、 Forrester[31]、Parr[110]以及刘俊[106]等在验证约束处理方法时，也主要采用了2维Branin-Hoo函数等简单算例。但这些函数其实并不是优化算法领域的最具挑战性的例子，还不能全面验证代理优化作为一种优化算法的性能。最近，文献[113，115]采用了更具代表性和挑战性的Rosenbrock函数算例、Rastrigin函数算例、7维G9函数算例、5维Himmelblau算例、Pressure Vessel Design等单目标优化标准算例，以及FON和ZET多种多目标优化标准算例，对代理优化算法的效率和精度进行了系统地验证和确认，而且掌握了代理优化算法的一些特性，总结了一些最佳参数设置。为了不断改进代理优化算法的性能，今后还需要采用更多的标准算例进行测试(例如文献[116]中给出了175种算例)。限于篇幅，下文仅给出了最具代表性的Rosenbrock函数和G9函数的最新测试结果。

Rosenbrock函数算例[117]是测试优化算法的经典算例之一。该函数最优点位于一个狭长而平坦的峡谷内(如图 11所示)。2维Rosenbrock函数算例优化数学模型为

Minf(x1,x2)=(1.0-x1)2+

s.t.x1,x2∈[-2.0,2.0]

(80)

图12给出了采用不同加点准则时，真实目标函数值的收敛情况。可见，对于单独使用的加点准则，EI、局部EI和LCB效果较好，MSP、PI和MSE效果不佳。如果组合使用，“MSP+EI”和“MSP+LCB”的效果均优于单独使用的效果。图13 给出了梯度增强型Kriging模型的优化收敛情况。可见引入梯度信息后，各种加点准则的收敛特性均得到改善；尤其是MSP准则的改善效果最明显。表 1为采用代理优化算法不同加点准则的优化结果的比较，表明代理优化算法不仅可以收敛到无约束问题的精确最优解，而且具有很高的效率。

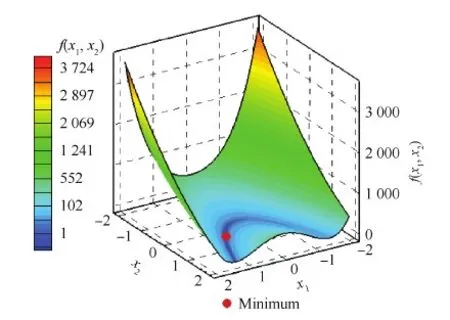
图11 二维Rosenbrock函数示意图Fig.11 Schematic of 2D Rosenbrock function

图12 代理优化算法不同加点准则收敛历程的比较(2维 Rosenbrock函数算例)Fig.12 Comparison of SBO convergence history with different infill sampling criteria for a 2D Rosenbrock function case

为了验证代理优化对更高维问题的适用性，可以采用多维Rosenbrock函数：

(81)

该函数在3维以上为多极值问题。

图14给出了针对5～80维函数，基于Kriging和梯度增强型Kriging模型的代理优化结果的比较。可以看出，对于Kriging模型，随着设计变量数增加，需要的函数计算次数迅速增加；而引入梯度信息后，函数计算次数对设计变量数变得不敏感。如果用于气动优化设计问题，采用Adjoint方法计算梯度，则可大大提高代理优化对高维问题的适应性。但需要说明的是，随着设计变量数增加，模型相关矩阵的阶数增加(n个样本，m个设计变量，矩阵阶数为n+n×m)，从而导致模型训练的计算量大幅度增加。因此，发展更高效的模型训练方法或矩阵降阶方法，成为今后一个值得关注的关键问题。

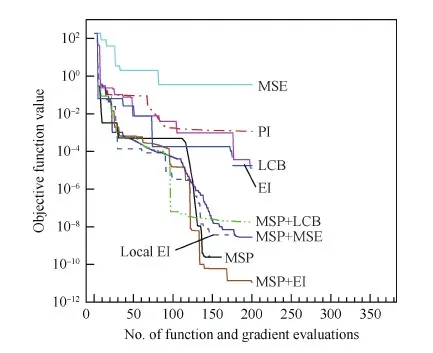
图13 引入梯度信息后的代理优化算法不同加点准则目标函数收敛历程的比较(2维Rosenbrock函数算例)Fig.13 Comparison of SBO convergence history incorporating gradient-information with different infill sampling criteria for a 2D Rosenbrock function case

表1 不同优化算法优化结果的比较(2维Rosenbrock函数算例)Table 1 Comparison of optimization results of different optimization algorithms for a 2D Rosenbrock function case

OptimizationalgorithmOptimalobjectivefunctionvalueNo.offunctionandgradientevaluationsTrue0NotapplicableKrigingMSP1.2358300fKrigingEI8.1681×10-6300fKrigingPI4.4276300fKrigingMSE3.4450×10-2300fKrigingLCB6.8738×10-5300fKrigingMSP+EI2.7596×10-7300fKrigingMSP+LCB1.4811×10-5300fKrigingMSP+MSE1.7529×10-3300fKriginglocalEI1.1496×10-8300fGEKMSP2.3888×10-10200f+200gGEKEI1.7859×10-5200f+200gGEKPI1.1485×10-3200f+200gGEKMSE3.5909200f+200gGEKLCB1.3395×10-5200f+200gGEKMSP+EI1.1157×10-11200f+200gGEKMSP+LCB1.7690×10-8200f+200gGEKMSP+MSE2.7855×10-9200f+200gGEKlocalEI3.7717×10-9200f+200g

Notes: f—function evaluation; g—gradient evaluation

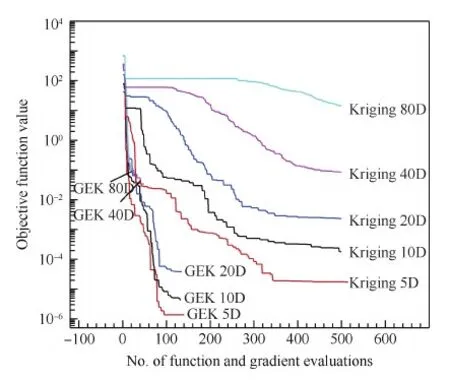
图14 5～80维Rosenbrock函数代理优化Kriging模型和GEK模型的比较Fig.14 Comparison of Kriging and GEK models for 5-80 dimensional Rosenbrock functions surrogate optimization

G9函数算例是国际上用于测试全局优化算法的一个经典算例。该算例含7个变量，4个约束(其中g1和g4为主动约束)，优化数学模型为

Minf(x)=(x1-10)2+5(x2-12)2+

4x6x7-10x6-8x7

(82)

该优化问题是一个难度非常大的全局优化问题[118]，原因在于：① 可行域很小，仅占整个设计空间的0.5%，属于强约束问题；② 目标函数的变化幅度较大，从107量级到103量级。目前为止，国际上能得到的最优解为

x*={2.330 499,1.951 372,-0.477 541 4,

4.365 726,-0.624 487 0,1.038 161,

1.594 227}

f(x*)=680.630 057 3

表2中给出了采用Kriging和GEK模型不同加点准则的优化效率比较。可见，MSP准则和LCB准则在未得到全局最优解前满足了优化终止条件；EI和局部EI方法的结果均非常接近全局最优；采用不同组合加点准则，只有“MSP+EI”收敛到了全局最优。引入梯度信息后，代理优化不同加点准则的优化结果和优化效率均得到显著改善，但仍然只有EI、局部EI、“MSP+EI”准则获得了全局最优解。此外，代理优化的结果不仅优于直接遗传算法优化的结果，且调用真实函数分析次数小了1～2个量级。

表3给出了代理优化结果与目前国际上能得到的最佳结果的比较，说明优化结果已经非常接近国际上最佳结果，主动约束得到精确满足。事实上，表中的国外最佳结果对g4约束是有所放宽的。这说明代理优化算法针对复杂全局优化问题具有很强的约束处理能力。

通过各种约束和无约束、局部和全局优化的标准算例测试，充分说明代理优化算法具有精确收敛到优化问题的真实最优解的能力。

4.2 气动优化设计标准算例确认

为了考查代理优化算法在实际工程优化问题中的性能，文献[119-120]开展了针对标准气动优化设计算例的确认研究，并与同类方法进行了比较。2015年，AIAA航空宇航科学大会(ASM)专门设立了气动设计优化讨论组(ADODG)，并定义了5个标准算例，包括2个翼型设计、2个机翼设计和1个全机优化设计算例。文献[119-120]采用了前2个标准算例：NACA0012和RAE2822翼型减阻优化设计。虽然NACA0012和RAE2822翼型已广泛被国内外研究人员作为展示气动优化设计算法的算例，但这些算例的设计状态和优化模型缺乏统一的定义，从而无法在同一尺度下评判所采用的优化算法的优劣。AIAA气动设计优化讨论组定义的RAE2822翼型的设计状态为：Ma=0.734，Re=6.5×106，优化数学模型为

表2 不同优化算法优化结果的比较(7维G9函数算例)Table 2 Comparison of optimization results of different optimization algorithms for a 7D G9 function case

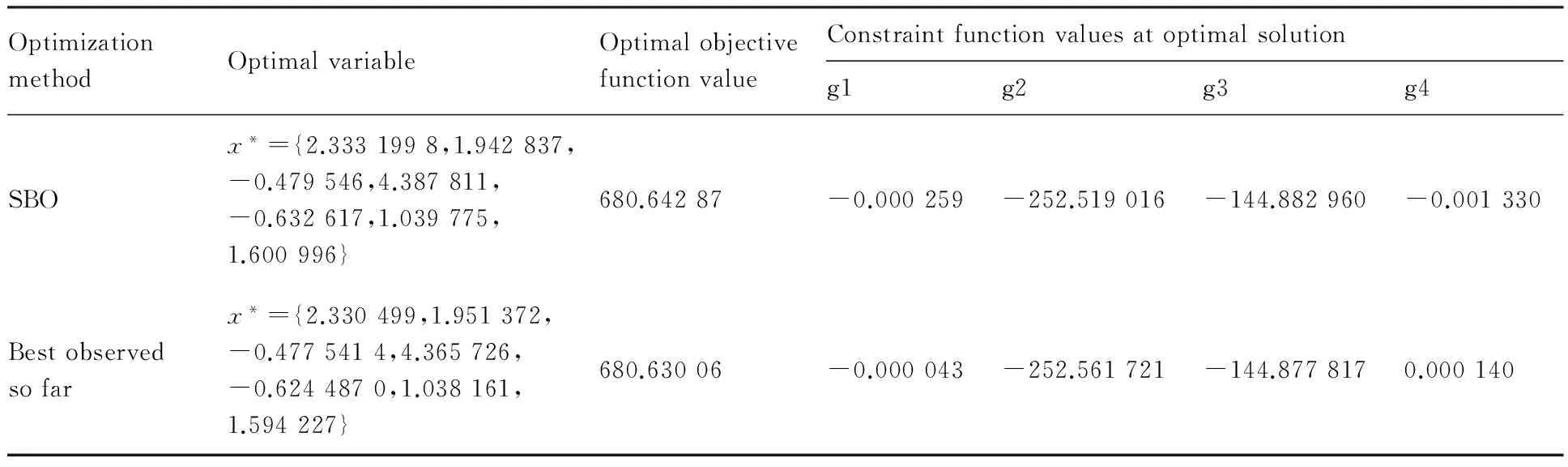
表3 7维G9函数优化结果 (EI加点准则)Table 3 Optimum results of a 7D G9 function case(EI infill-sampling criterion)

MinCD

(83)

式中：CL、CD和Cm分别为翼型的升力、阻力和俯仰力矩系数；A1和A0分别为优化翼型和初始翼型的面积。ADODG还要求必须对基准翼型和优化翼型作网格收敛性研究，并且要证明优化过程充分收敛。

文献[120]采用CST(Class-function Shape-function Transformation)方法作为翼型外形参数化方法，并采用8阶伯恩斯坦多项式，共18个设计变量。对初始翼型作了网格收敛性研究(见表4)，最后确定计算网格数量大约为13万(513×257)。如图 15所示，网格远场边界为90c(c为翼型弦长)；物面第1层网格高度为2.0×10-6。为了避免升力等式约束，文献将升力约束改为升力不减，并固定迎角α=2.879 5°。

表4基准RAE2822翼型气动性能网格收敛性

Table4GridconvergenceforbaselineRAE2822airfoilaerodynamicperformance

GridsizeCL/countsCD/counts192×9682.4221.66256×12882.4208.10320×16082.4201.85384×19282.4198.65448×22482.4196.53512×25682.4195.02576×28882.4194.09

图15 RAE2822翼型计算网格示意图 Fig.15 Schematic of computational grid for RAE2822 airfoil

表5给出了优化翼型的气动性能及面积与基准翼型的比较。在所有约束都得到精确满足的前提下，阻力大大降低。与文献[119]中梯度优化结果的比较说明，代理优化结果明显优于梯度优化结果。图16给出了代理优化过程中目标函数阻力系数的收敛历程。共进行了3轮优化，通过第2轮和第3轮优化，阻力分别进一步下降了0.5个counts和0.2个counts，说明优化已经充分收敛。图17给出了优化前后翼型的几何形状及压力系数Cp分布对比。优化后上表面的强激波被削弱成两道非常弱的激波，优化效果显著。按ADODG的要求还给出了优化翼型的网格收敛性研究(表6)，发现优化翼型最终阻力为102.98 counts，这个结果优于国际同行的结果[121]。

表5优化前后翼型的气动性能及面积对比

Table5Comparisonofaerodynamicperformanceandareaofbaselineandoptimumairfoils

AirfoilCL/countsCD/countsCmA1RAE282282.4195.00-0.092130.07794Optimizedbygradientmethod[119]82.4129.40-0.091900.07794OptimizedbySBO82.4104.29-0.088020.07794

图16 RAE2822翼型减阻优化收敛历程 Fig.16 Convergence history of drag reduction optimization for RAE2822 airfoil

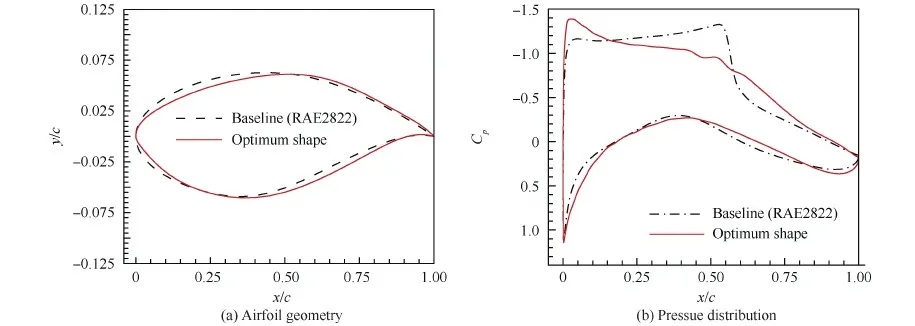
图17 优化前后翼型的压力分布及几何形状比较Fig.17 Comparison of pressure distributions and geometries for baseline and optimum airfoils

表6优化翼型气动性能网格收敛性

Table6Gridconvergenceforoptimumairfoilaerodynamicperformance

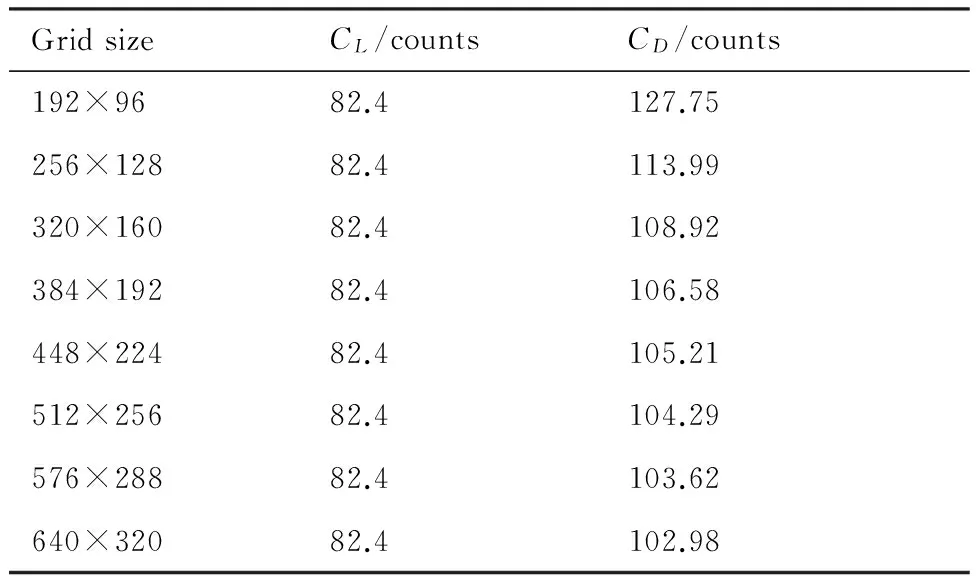
GridsizeCL/countsCD/counts192×9682.4127.75256×12882.4113.99320×16082.4108.92384×19282.4106.58448×22482.4105.21512×25682.4104.29576×28882.4103.62640×32082.4102.98

为了更进一步确认代理优化算法在三维复杂外形气动设计中的优化能力，下一步需要进行ADODG定义的算例3[121]、算例4[122-123]和算例5[124]的NASA CRM标准机翼和全机模型的代理优化设计研究，并与梯度优化方法[122-123]的结果进行比较。更多新的结果将可能在2017年的第3届ADODG研讨会上展示。

4.3 气动/结构综合优化设计算例确认

具有学科强耦合关系的气动/结构综合优化设计，是飞机MDO的最典型问题[125]。该算例可以用于确认代理优化算法在具有学科强耦合关系的飞行器精细化优化设计中的适用性。文献[81,126]采用代理优化算法研究了某高亚声速运输机翼身组合体(如图 18所示)机翼气动/结构综合优化。但受到当时技术条件限制，只采用了8个气动和结构学科的设计变量。最近，文献作者又采用最新的代理优化算法，得到了23个设计变量下的优化设计结果。优化数学模型为

MinW

(84)

式中：W为机翼质量；L和L/D分别为组合体升力和升阻比；σmax和δmax分别为机翼结构的最大应力和变形。该优化是对巡航状态下的机翼进行设计：通过调整迎角、机翼尖梢比、线性扭转角以及上下蒙皮沿展向各段厚度(各10个变量)共23个设计变量，在满足升力、升阻比以及最大应力和翼尖最大变形约束的条件下，获得最小的机翼结构重量。该优化的机翼气动/结构分析模型参见文献[81，126]：气动分析采用全速势有黏/无黏迭代的方法；采用ANSYS软件进行结构分析；用弱耦合法进行静气动弹性分析。

图18 高亚声速运输机翼身组合体外形图 Fig.18 Schematic of a wing-body configuration for high-subsonic transport aircraft

表7给出了优化机翼相对于基准机翼的性能变化，图19给出了代理模型优化过程中目标函数的收敛历程。优化以200个样本点为基础建立代理模型，加点准则采用 “MSP+EI”组合方法。可以看出，在严格满足升力、升阻比、最大应力和变形约束的情况下，机翼重量降低了28.9%。这说明所采用的代理优化方法不仅优化效率高(23个设计变量问题只进行不到300次的多学科耦合分析)、优化效果良好，且能够精确处理气动和结构不同学科的约束。图 20给出了优化后的机翼变形图。图 21给出了优化前后机翼上下蒙皮厚度尺寸的对比，优化后的机翼厚度尺寸大大降低，从翼根到翼梢厚度变化更加平缓，优化结果比较合理，优化效果非常显著。

通过该算例确认，表明代理优化方法在处理具有复杂耦合关系的飞行器复杂多学科精细化优化设计问题方面具有良好的发展前景。但是，随着设计变量数的增加，优化的计算量将会迅速增加。而引入气动/结构耦合系统Adjoint梯度[127]，以及成本更低的低可信度分析，发展梯度增强型变可信度Kriging代理模型及其相应的代理优化算法，将是该领域未来重点发展的方向之一。代理优化算法的研究也将继续成为未来 10～20年内飞行器精细优化设计领域的研究热点。

表7优化前后机翼外形及性能对比

Table7Comparisonofshapeandperformanceofbaselineandoptimumwing

WingperformanceBaselineOptimizedTaperratio0.210.21Lineartwistangle/(°)-2.49-4.00Angleofattack/(°)0.821.03Wingweight(single)/kg2030.31311.1Lift/t61345.854003.4(≥54)Lift-dragratio27.5627.01(≥27)Maxequivalentstress/(108Pa)2.73272.7282Maxdeformationatwingtip/m0.9470.998(≤1)

图19 机翼气动/结构综合优化过程中目标函数收敛曲线Fig.19 Convergence history of objective function for wing aerostructural optimization

图20 优化机翼变形前后对比Fig.20 Comparison of optimum wings (un-deformed and deformed)

图21 优化前后机翼蒙皮厚度对比 Fig.21 Comparison of skin thickness of baseline and optimum wings

5 结 论

本文介绍了Kriging模型的基本理论和算法，包括梯度增强型Kriging、CoKriging和分层Kriging等研究新进展。从一种通用优化算法的角度，阐述了基于Kriging模型的代理优化算法的原理和算法框架，介绍了优化加点准则和子优化的研究进展,讨论了常用的几种优化加点准则、约束处理方法和优化终止条件。介绍了代理优化算法标准算例验证和确认的研究进展。

1) 基于Kriging模型的代理优化算法，能够精确收敛到优化问题的真实最优解，且具有精确的约束处理能力。因而可以作为一种通用优化算法，应用于具有光滑、连续设计空间的任意优化问题。

2) 代理优化算法的优化机制，是通过代理模型及其子优化过程来产生新的样本点。

3) 加点准则及其子优化问题求解是基于Kriging模型的代理优化算法的关键。MSP准则偏向局部探测；EI、LCB准则在全局探索和局部探测之间取得很好折中；PI和MSE准则偏重于全局探索，收敛速度很慢，不适合单独使用。将MSP与EI、LCB或MSE同时混合使用，成为更加实用的方法；已有的算例测试表明，“MSP+EI”组合加点准则的综合性能最佳。

4) 基于Kriging模型的代理优化算法既适用于局部优化问题，又适用于全局最优解。对于全局优化问题，优化效率比遗传算法可提高1～2个量级。

5) 对于梯度可以快速获得的问题，引入梯度信息来建立梯度增强Kriging模型，不仅可大幅度提高优化效率，而且能改善优化精度。

6) 基于Kriging模型的代理优化算法对于20维左右的工程设计问题已经基本成熟，在保证优化质量的同时，能实现很高的优化效率。

基于Kriging模型的代理优化算法存在如下关键问题值得进一步研究：

1) 维度之咒。对于30个以上设计变量的高维度优化问题，优化效率较低。

2) 大规模样本数据问题。如果优化过程中产生大量样本点(2 000以上)，针对这些样本点进行代理模型训练的时间甚至超过精确数值分析的时间。

3) 对于梯度增强Kriging模型，随着设计变量数增加，模型训练的时间大大增加。

4) 复杂设计空间问题。主要针对设计空间呈超多极值、高度非线性、强烈振荡等特性的复杂优化问题。

5) 数值噪声问题。样本数据计算可能未充分收敛，这样便带有数值噪声，从而对代理优化的过程和结果产生重要影响。

经过文献调研，作者认为今后在代理优化方法研究方面还需要开展的工作如下：

1) 通过同时引入Adjoint梯度和低可信度分析，发展适用于大规模设计变量问题的模型训练及高效代理优化算法。

2) 研究适用于大规模样本数据的数据分区技术及相应的代理优化算法。

3) 研究局部代理模型和全局代理模型相结合的方法，克服代理模型刚性和局部收敛精度差的问题。

4) 研究新的加点准则及其子优化方法，例如研究可同时加任意N个样本点的算法，提高并行优化性能。

5) 研究数据库辅助的高效代理优化算法。充分运用分析和优化工作过程产生的大量历史数据，甚至包括风洞试验得到的试验数据，对进一步的优化设计形成强有力的数据支持。

6) 研究代理优化算法在复杂系统多学科优化设计问题的应用。包括具有大规模设计变量和大规模约束，且各学科之间具有复杂耦合关系的工程设计问题。

致 谢

感谢德国宇航中心(DLR)Goertz博士、布伦瑞克工业大学Zimmermann博士、凯泽斯劳滕大学Gauger教授。同时也感谢荷兰代尔夫特工业大学Dwight教授、美国爱荷华州立大学Leifsson教授。他们与作者就本文工作进行了大量讨论并给予了许多建议。本文撰写历时2年多，感谢课题组的老师和同学们在这期间对本文撰写的大力协助和支持。

[1] HERNANDEZ S. Structural optimization: 1960—2010 and beyond[J]. Computational Technology Reviews, 2010, 2: 177-222.

[2] SCHMIT L A. Structural design by systematic synthesis[C]//Second Conference on Electronic Computation. Pittsburg: ASCE, 1960: 105-132.

[3] HICKS R M, MUNNAN E M, VANDERPLAATS G N. An assessment of airfoil design by numerical optimization: NASA TM X-3092[R]. Washington, D.C.: NASA, 1974.

[4] HICKS R M, HENNE P A. Wing design by numerical optimization[J]. Journal of Aircraft, 1978, 15(7): 407-412.

[5] SOBIESZCZANSKI-SOBIESKI J, HAFTKA R T. Multidisciplinary aerospace design optimization: Survey of recent developments[J]. Structural Optimization, 1997, 14(1): 1-23.

[6] KROO I, ALTUS S, BRAUN R, et al. Multidisciplinary optimization methods for aircraft preliminary design: AIAA-1994-4325[R]. Reston: AIAA, 1994.

[7] AIAA MDO Technical Committee. Current state of the art: Multidisciplinary design optimization: AIAA White Paper[R]. Reston: AIAA, 1991.

[8] ZHANG K S, HAN Z H, LI W J, et al. Bilevel adaptive weighted sum method for multidisciplinary multi-objective optimization[J]. AIAA Journal, 2008, 46(10): 2611-2622.

[9] 余雄庆. 飞机总体多学科设计优化的现状与发展方向[J]. 南京航空航天大学学报, 2008, 40(4): 417-426.

YU X Q. Multidisciplinary design optimization for aircraft conceptual and preliminary design: Status and directions[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2008, 40(4): 417-426 (in Chinese).

[10] 穆雪峰， 姚卫星， 余雄庆, 等. 多学科设计优化中常用代理模型的研究[J]. 计算力学学报, 2005, 22(5): 608-612.

MU X F, YAO W X, YU X Q, et al. A survey of surrogate models used in MDO[J]. Chinese Journal of Computational Mechanics, 2005, 22(5): 608-612 (in Chinese).

[11] VIANA F A C, SIMPSON T W, BALABANOV V, et al. Metamodeling in multidisciplinary design optimization: how far have we really come?[J]. AIAA Journal, 2014, 52(4): 670-690.

[12] 张健, 李为吉. 飞机多学科设计优化中的近似方法分析[J]. 航空计算技术, 2005, 35(3): 5-8.

ZHANG J, LI W J. Approximation methods analysis in multidisciplinary design optimization[J]. Aeronautical Computer Technique, 2005, 35(3): 5-8 (in Chinese) .

[13] HAN Z H, GOERTZ S. A hierarchical Kriging model for variable-fidelity surrogate modeling[J]. AIAA Journal, 2012, 50(3): 1885-1896.

[14] HAN Z H, ZIMMERMANN R, GOERTZ S. An alternative CoKriging model for variable-fidelity surrogate modeling[J]. AIAA Journal, 2012, 50(5): 1205-1210.

[15] HAN Z H, ZHANG K S. Surrogate-based optimization[M]. InTech Book, 2012: 343-362.

[16] SCHMIT L A, FARSHI B. Some approximation concepts for structural synthesis[J]. AIAA Journal, 1974, 12(5): 692-699.

[17] GIUNTA A A, WATSON L T. A Comparison of approximation modeling techniques: Polynomial versus interpolation models: AIAA-1998-4758[R]. Reston: AIAA, 1998.

[18] KOCH P N, SIMPSON T W, ALLEN J K, et al. Statistical approximations for multidisciplinary design optimization: the problem of the size[J]. Journal of Aircraft, 1999, 36(1): 275-286.

[19] SEVANT N E, BLOOR M I G, WILSON M J. Aerodynamic design of a flying wing using response surface methodology[J]. Journal of Aircraft, 2000, 37(4): 562-569.

[20] JEONG S, MURAYAMA M, YAMAMOTO K. Efficient optimization design method using Kriging model[J]. Journal of Aircraft, 2005, 42(2): 413-420.

[21] VAVALLE A, QIN N. Iterative response surface based optimization scheme for transonic airfoil design[J]. Journal of Aircraft, 2007, 44(2): 365-376.

[22] KRIGE D G. A statistical approach to some basic mine valuations problems on the witwatersrand[J]. Journal of the Chemical, Metallurgical and Mining Engineering Society of South Africa, 1951, 52(6): 119-139.

[23] SACKS J, WELCH W J, MITCHELL T J, et al. Design and analysis of computer experiments[J]. Statistical Science, 1989, 4(4): 409-423.

[24] POWELL M J D. Algorithms for approximation[M]. New York: Oxford University Press, 1987: 141-167.

[25] BUHMANN M D. Acta numerica[M]. New York: Cambridge University Press, 2000: 1-38.

[26] KRISHNAMURTHY T. Response surface approximation with augmented and compactly supported radial basis functions: AIAA-2003-1748[R]. Reston: AIAA, 2003.

[27] MULLUR A A, MESSAC A. Extended radial basis functions: more flexible and effective metamodeling[J]. AIAA Journal, 2005, 43(6): 1306-1315.

[28] PARK J, SANDBERG I W. Universal approximation using radial-basis-function networks[J]. Neural Computation, 1991, 3(2): 246-257.

[29] ELANAYAR S V T, SHIN Y C. Radial basis function neural network for approximation and estimation of nonlinear stochastic dynamic systems[J]. IEEE Transactions on Neural Networks, 1994, 5(4): 594-603.

[30] SMOLA A J, SCHÖLKOPF B. A tutorial on support vector regression[J]. Statistics and Computing, 2004, 14(3): 199-222.

[31] FORRESTER A I J, KEANE A J. Recent advances in surrogate-based optimization[J]. Progress in Aerospace Sciences, 2009, 45(1): 50-79.

[32] WANG Q, MOIN P, IACCARINO G. A rational interpolation scheme with super-polynomial rate of convergence[J]. SIAM Journal of Numerical Analysis, 2010, 47(6): 4073-4097.

[33] WANG Q, MOIN P, IACCARINO G. A high-order multi-variate approximation scheme for arbitrary data sets[J]. Journal of Computational Physics, 2010, 229(18): 6343-6361.

[34] WIENER N. The homogeneous chaos[J]. American Journal of Mathematics, 1938, 60(4): 897-936.

[35] XIU D. Numerical methods for stochastic computations: A spectral method approach[M]. Princeton: Princeton University Press, 2010: 152.

[36] QUEIPO N V, HAFTKA R T, SHYY W, et al. Surrogate-based analysis and optimization[J]. Progress in Aerospace Sciences, 2005, 41(1): 1-28.

[37] FORRESTER A I J, SBESTER A, KEANE A. Engineering design via surrogate modeling: A practical guide[M]. Chichester: John Wiley & Sons, 2008.

[38] KEANE A J, NAIR P B. Computational approaches for aerospace design: The pursuit of excellence[M]. Chichester: John Wiley & Sons, 2005.

[39] GIUNTA A A, WOJTKIEWICZ J S F, ELDRED M S. Overview of modern design of experiments methods for computational simulations: AIAA-2003-649[R]. Reston: AIAA, 2003.

[40] FANG K T, LIN D, WINKER P, et al. Uniform design: Theory and application[J]. Technometrics, 2000, 42(3): 237-248.

[41] MATHERON G M. Principles of geostatistics[J]. Economic Geology, 1963, 58(8): 1246-1266.

[42] MATHERON G. Theory of regionalized variable and its applications[M]. Fontainebleau: Ecole des Mines, 1971.

[43] SIMPSON T W, MAUERY T M, KORTE J J, et al. Kriging models for global approximation in simulation-based multidisciplinary design optimization[J]. AIAA Journal, 2001, 39(12): 2233-2241.

[44] MARTIN J D, SIMPSON T W. Use of Kriging models to approximate deterministic computer models[J]. AIAA Journal, 2005, 43(4): 853-863.

[45] TOAL D J J, BRESSLOFF N W, KEAN A J. Kriging hyperparameter tuning strategies[J]. AIAA Journal, 2008, 46(5): 1240-1252.

[46] 王晓锋, 席光. 基于Kriging模型的翼型气动性能优化设计[J]. 航空学报, 2005, 26(5): 545-549.

WANG X F, XI G. Aerodynamic optimization design for airfoil based on Kriging model[J]. Acta Aeronautica et Astronautica Sinica, 2005, 26(5): 545-549 (in Chinese).

[47] 许瑞飞， 宋文萍， 韩忠华. 改进Kriging模型在翼型气动优化设计中的应用研究[J]. 西北工业大学学报, 2010， 28(4)： 503-510.

XU R F, SONG W P, HAN Z H. Application of improved kriging-model-based optimization method in airfoil aerodynamic design[J]. Journal of Northwestern Polytechnical University, 2010， 28(4)： 503-510 (in Chinese).

[48] LIU J, HAN Z H, SONG W P. Efficient kriging-based optimization design of transonic airfoils: Some key issues: AIAA-2012-0967[R]. Reston: AIAA, 2012.

[49] 孙俊峰, 刘刚, 江雄, 等. 基于Kriging模型的旋翼翼型优化设计研究[J]. 空气动力学学报, 2013, 31(4): 437-441.

SUN J F, LIU G, JIANG X, et al. Research of rotor airfoil design optimization based on the Kriging model[J]. Acta Aerodynamica Sinica, 2013, 31(4): 437-441 (in Chinese).

[50] HAN Z H, LIU J, SONG W P, et al. Surrogate-based aerodynamic shape optimization with application to wind turbine airfoils: AIAA-2013-1108[R]. Reston: AIAA, 2013.

[51] 白俊强, 王波, 孙智伟, 等. 基于松散式代理模型管理框架的亚音速机翼优化设计方法研究[J]. 西北工业大学学报, 2011, 29(4): 515-519.

BAI J Q, WANG B, SUN Z W, et al. Developing optimization design of subsonic wing with losse type of agent model[J]. Journal of Northwestern Polytechnical University, 2011, 29(4): 515-519 (in Chinese).

[52] 孙美建, 詹浩. Kriging模型在机翼气动外形优化中的应用[J]. 空气动力学学报, 2011, 29(6): 759-764.

SUN M J, ZHAN H. Application of Kriging surrogate model for aerodynamic shape optimization of wing[J]. Acta Aerodynamica Sinica, 2011, 29(6): 759-764 (in Chinese).

[53] 何欢, 朱广荣, 何成, 等. 基于Kriging模型的结构耐撞性优化[J]. 南京航空航天大学学报, 2014, 46(2): 297-303.

HE H, ZHU G R, HE C, et al. Crashworthiness optimization based on Kriging metamodeling[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2014, 46(2): 297-303 (in Chinese).

[54] 刘克龙, 姚卫星, 穆雪峰. 基于Kriging代理模型的结构形状优化方法研究[J]. 计算力学学报, 2006, 23(3): 344-347, 362.

LIU K L, YAO W X, MU X F. A method of structural shape optimization based on Kriging model[J]. Chinese Journal of Computational Mechanics, 2006, 23(3): 344-347, 362 (in Chinese).

[55] 杨军, 刘勇琼, 艾春安, 等. 改进Kriging模型在固冲发动机导弹气动优化设计中的应用[J]. 固体火箭技术, 2013, 36(5): 590-593.

YANG J, LIU Y Q, AI C A, et al. Application of improved Kriging-model-based optimization method in solid rocket-ramjet missile’s aerodynamic design[J]. Journal of Solid Rocket Technology, 2013, 36(5): 590-593 (in Chinese).

[56] 孙凯军, 宋文萍, 韩忠华. 基于Kriging模型的高超声速舵面优化设计[J]. 航空计算技术, 2012, 42(2): 9-12.

SUN K J, SONG W P, HAN Z H. Optimization design of hypersonic control surface based on Kriging model[J]. Aeronautical Computing Technique, 2012, 42(2): 9-12 (in Chinese).

[57] 郑侃, 廖文和, 张翔. 基于近似模型管理的微小卫星结构多目标优化设计[J]. 中国机械工程, 2012, 23(6): 655-659.

ZHENG K, LIAO W H, ZHANG X. Multi-objective optimization design for microsatellite structure based on approximation model management[J]. China Mechanical Engineering, 2012, 23(6): 655-659 (in Chinese).

[58] 姚拴宝， 郭迪龙， 孙振旭， 等. 基于Kriging代理模型的高速列车头型多目标优化设计[J]. 中国科学, 2013, 43(2): 186-200.

YAO S B, GUO D L, SUN Z X, et al. Multi-objective optimization of the streamlined head of high-speed trains based on the kriging model[J]. Science China, 2013, 43(2): 186-200 (in Chinese).

[59] 韩永志, 高行山, 李立州. 基于Kriging模型的涡轮叶片多学科设计优化[J]. 航空动力学报, 2007, 22(7): 1055-1059.

HAN Y Z， GAO X S, LI L Z. Kriging model-based multidisciplinary design optimization for turbine blade[J]. Journal of Aerospace Power, 2007, 22(7): 1055-1059 (in Chinese).

[60] 张科施, 韩忠华, 李为吉, 等. 基于近似技术的高亚声速运输机机翼气动/结构优化设计[J]. 航空学报, 2006, 27(5): 810-815.

ZHANG K S, HAN Z H, LI W J, et al. Multidisciplinary aerodynamic/structural design optimization for high subsonic transport wing using approximation technique[J]. Acta Aeronautica et Astronautica Sinica, 2006, 27(5): 810-815 (in Chinese).

[61] SUN W Y, YUAN Y X. Optimization theory and methods: nonlinear programming[M]. New York: Springer Ebooks, 2006.

[62] HOLLAND J H. Adaptation in natural and artificial systems[M]. Ann Arbor: The University of Michigan Press, 1975.

[63] SLOTNICK J, KHODADOUST A, ALONSO J, et al. CFD vision 2030 study: A path to revolutionary computational aerosciences: NASA/CR-2014-218178[R]. Washington, D.C.: NASA Langley Research Center, 2014.

[64] 吴宽展， 刘学军， 吕宏强. 超临界翼型设计中的多响应代理模型[J]. 航空计算技术, 2014, 44(4): 17-22.

WU K Z, LIU X J, LV H Q. Multi-output surrogate model in supercritical airfoil design[J]. Aeronautical Computing Technique, 2014, 44(4): 17-22 (in Chinese).

[65] ZIMMERMANN R. On the condition number anomaly of gaussian correlation matrices[J]. Linear Algebra and its Applications, 2015, 466: 521-526.

[66] VIANA F A, HAFTKA R T, STEFFEN V. Multiple surrogates: How cross-validation errors can help us to obtain the best predictor?[J]. Structural and Multidisciplinary Optimization, 2009, 39(4): 439-457.

[67] KOBLEWALIK J, OSBORNE M R. Methods for unconstrained optimization problems[M]. New York: Elsevier, 1968.

[68] NELDER J A, MEAD R. A simple method for function minimization[J]. The Computer Journal, 1965, 7(4): 308-313.

[69] LOPHAVEN S N, NIELSEN H B, SØNDERGAARD J. DACE—A MATLAB Kriging toolbox (version 2.0): IMM-REP-2002-12[R]. Lyngby: Informatics and Mathematical Modelling, Technical University of Denmark, 2002.

[70] YIN J, NG S H, NG K M. Kriging meta model with modified nugget-effect: The heteroscedastic variance case[J]. Computers Industrial Engineering, 2011, 61(3): 760-777.

[71] FORRESTER A I J, KEANE A J, BRESSLOFF N W. Design and analysis of noisy computer experiments[J]. AIAA Journal, 2006, 44(10): 2331-2339.

[72] ETMAN L F P. Design and analysis of computer experiments: The Method of Sacks et al： Engineering Mechanics report WFW 94-098[R]. Eindhoven, The Netherlands: Eindhoven University of Technology, 1994.

[73] OSIO I G, AMON C H. An engineering design methodology with multistage bayesian surrogate and optimal sampling[J]. Research in Engineering Design, 1996, 8(4): 189-206.

[74] JONES D R, SCHONLAU M, WELCH W J. Efficient global optimization of expensive black-box functions[J]. Journal of Global Optimization, 1998, 13(4): 455-492.

[75] COX D D, JOHN S. SDO: A statistical method for global optimization[C]//IEEE International Conference on Systems, Man & Cybernetics, 1992: 1241-1246.

[76] TORCZON V, TROSSET M W. Use approximation to accelerate engineering design optimization: AIAA-1998-4800[R]. Reston: AIAA, 1998.

[77] BOOKER A J. Design and analysis of computer experiments: AIAA-1998-4757[R]. Reston: AIAA, 1998.

[78] MECKESHEIMER M, BARTON R R, SIMPSON T, et al. Metamodeling of combined discrete/continuous responses[J]. AIAA Journal, 2001, 39(10): 1950-1959.

[79] CHEN S K, XIONG Y, CHE W. Multiresponse and multistage metamodeling approach for design optimization[J]. AIAA Journal, 2009, 47(1): 206-218.

[80] HAN Z H, ZHANG K S, SONG W P, et al. Optimization of active flow control over an airfoil using a surrogate-management framework[J]. Journal of Aircraft, 2010, 47(2): 603-612.

[81] ZHANG K S, HAN Z H, LI W J, et al. Coupled aerodynamic/structural optimization of a subsonic transport wing using a surrogate model[J]. Journal of Aircraft, 2008, 45(6): 2167-2171.

[82] CHUNG J J, ALONSO H S. Using gradients to construct cokriging approximation models for high-dimensional design optimization problems： AIAA-2002-0317[R]. Reston: AIAA, 2002.

[83] CHUNG J J, ALONSO H S. Design of a low-boom supersonic business jet using cokriging approximation models: AIAA-2002-5598[R]. Reston: AIAA, 2002.

[84] LIU W, BATILL S M. Gradient-enhanced response surface approximations using kriging models: AIAA-2002-5456[R]. Reston: AIAA, 2002.

[85] LAURENCEAU J, SAGAUT P. Building efficient response surfaces of aerodynamic functions with Kriging and Cokriging[J]. AIAA Journal, 2008, 46(2): 498-507.

[86] JAMESON A. Optimum aerodynamic design using cfd and control theory: AIAA-1995-1729[R]. Reston: AIAA, 1995.

[87] DWIGHT R, HAN Z H. Efficient uncertainty quantification using gradient enhanced Kriging: AIAA-2009-2276[R]. Reston: AIAA, 2009.

[88] HAN Z H, GOERTZ S, ZIMMERMANN R. Improving variable-fidelity surrogate modeling via gradient-enhanced Kriging and a generalized hybrid bridge function[J]. Aerospace Science and Technology, 2013, 25(1): 177-189.

[89] YAMAZAKI W, RUMPFKEIL M P, MAVRIPLIS D J. Design optimization utilizing gradient/hessian enhanced surrogate model: AIAA-2010-4363[R]. Reston: AIAA, 2010.

[90] HAN Z H. Improving adjoint-based aerodynamic optimization via gradient-enhanced Kriging: AIAA-2012-0670[R]. Reston: AIAA, 2012.

[91] DAVID M. Geostatistical ore reserve estimation[M]. Amsterdam: Elsevier, 1977: 1-364.

[92] JOURNEL A G, HUIJBREGTS J C. Mining geostatistics[M]. New York: Academic Press, 1978: 1-600.

[93] MYERS D E. Matrix formulation of Cokriging[J]. Mathematical Geology, 1982, 14(3): 249-257.

[94] GOOVAERTS P. Ordinary CoKriging revisited[J]. Mathematical Geology, 1997, 30(1): 21-42.

[95] PAPRITZ A. Standardized vs customary ordinary CoKriging: some comments on the article “the geostatistical analysis of experiments at the landscape-scale” by T.F.A. Bishop and R.M., Lark[J]. Geoderma, 2008, 146(1): 391-396.

[96] KENNEDY M C, O’HAGAN A. Predicting the output from a complex computer code when fast approximations are available[J]. Biometrika, 2000, 87(1): 1-13.

[97] QIAN Z, WU C F J. Bayesian hierarchical modeling for integrating low-accuracy and high-accuracy experiments[J]. Technometrics, 2008, 50(2):192-204.

[98] FORRESTER A I J, SBESTER A, KEANE A J. Multi-fidelity optimization via surrogate modeling[J]. Proceedings of the Royal Society A, Mathematical, Physical and Engineering Sciences, 2007, 463(2088): 3251-3269.

[99] KUYA Y, TAKEDA K, ZHANG X, et al. Multifidelity surrogate modeling of experimental and computational aerodynamic data sets[J]. AIAA Journal, 49(2): 289-298.

[100] ZIMMERMANN R, HAN Z H. Simplified cross-correlation estimation for multi-fidelity surrogate cokriging models[J]. Advance and Applications in Mathematical Sciences, 2010, 7(2): 181-201.

[101] HAN Z H, ZIMMERMANN R, GOERTZ S. A new CoKriging method for variable-fidelity surrogate modeling of aerodynamic data: AIAA-2010-1225[R]. Reston: AIAA, 2010.

[102] JOSEPH V R, HUNG Y, SUDJIANTO A. Blind Kriging: A new method for developing metamodels[J]. Journal of Mechanical Design, 2008, 130(3): 350-353.

[103] ZHAO L, CHOI K K, LE I. Metamodeling method using dynamic Kriging for design optimization[J]. AIAA Journal, 2011, 49(9): 2034-2046.

[104] LIANG H Q, ZHU M, WU Z. Using cross-validation to design trend function in Kriging surrogate modeling[J]. AIAA Journal, 2014, 52(10): 2313-2327.

[105] ANKENMAN B E, NELSON B L, STAUM J. Stochastic Kriging for simulation metamodeling[J]. Operations Research, 2010, 58(2): 371-382.

[106] LIU J, HAN Z H, SONG W P. Comparison of infill sampling criteria in kriging-based aerodynamic optimization[C]//28th Congress of the International Council of the Aeronautical Sciences, 2012.

[107] JONES D R. A taxonomy of global optimization methods based on response surfaces[J]. Journal of Global Optimization，2001, 21(4): 345-383.

[108] BOOKER A J, DENNIS J J, FRANK P D, et al. A rigorous framework for optimization of expensive functions by surrogates[J]. Structural Optimization, 1998, 17(1): 1-13.

[109] SASENA M J, PAPALAMBROS P Y, GOOVAERTS P. Exploration of metamodeling sampling criteria for constrained global optimization[J]. Engineering Optimization, 2002, 34(34): 263-278.

[110] PARR J M, KEANE J A, FORRESTER I J, et al. Infill sampling criteria for surrogate-based optimization with constraint handling[J]. Engineering Optimization , 2012, 44(10): 1147-1166.

[111] DEB K. An efficient constraint handling method for genetic algorithms[J]. Computer Methods in Applied Mechanics and Engineering, 2010, 186(2-4): 311-338

[112] ONG Y S, NAIR P B, KEANE A J. Evolutionary optimization of computationally expensive problems via surrogate modeling[J]. AIAA Journal, 2003, 41(4): 687-696.

[113] 刘俊. 基于代理模型的高效气动优化设计方法及应用[D]. 西安： 西北工业大学, 2015.

LIU J. Efficient surrogate-based optimization method and its application in aerodynamic design[D]. Xi’an: Northwestern Polytechnical University, 2015 (in Chinese).

[114] 高月华， 王希诚. 基于Kriging代理模型的多点加点序列优化方法[J]. 工程力学， 2012， 29(4): 90-95.

GAO Y H, WANG X C. A sequential optimization method with multi-point sampling criterion based on kriging surrogate mode[J]. Engineering Mechanics, 2012, 29 (4): 90-95 (in Chinese).

[115] 刘俊, 宋文萍, 韩忠华, 等. 梯度增强的Kriging模型与Kriging模型在优化设计中的比较研究[J]. 西北工业大学学报, 2015, 3(3): 819-826.

LIU J, SONG W P, HAN Z H, et al. Comparative study of gek (gradient-enhanced Kriging) and Kriging when applied to design optimization[J]. Journal of Northwestern Polytechnical University, 2015, 3(3): 819-826 (in Chinese).

[116] JAMIL M, YANG X S. A literature survey of benchmark functions for global optimization problems[J]. Journal of Mathematical Modelling and Numerical Optimisation, 2013, 4(2): 150-194.

[117] ROSENBROCK H H. An automatic method for finding the greatest or least value of a function[J]. The Computer Journal, 1960, 3(3): 175-184.

[118] MICHALEWICZ Z. Genetic algorithm, numerical optimization, and constraints[C]//Proceedings of the Sixth International Conference on Genetic Algorithms, 1995: 151-158.

[119] TESFAHUNEGN Y A, KOZIEL S, GRAMANZINI J R, et al. Application of direct and surrogate-based optimization to two-dimensional benchmark aerodynamic problems: A comparative study: AIAA-2015-0265[R]. Reston: AIAA, 2015.

[120] ZHANG Y, HAN Z H, SHI L X, et al. Multi-round surrogate-based optimization for benchmark aerodynamic design problems: AIAA-2016-1545[R]. Reston: AIAA, 2016.

[121] REN J, THELEN A, AMRIT A, et al. Application of multi-fidelity optimization techniques to benchmark aerodynamic design problems: AIAA-2016-1542[R]. Reston: AIAA, 2016.

[122] LYU Z, KENWAY G KW, MARTINS J R R A. Aerodynamic shape optimization studies on the common research model wing benchmark[J]. AIAA Journal, 2015, 53(4): 968-985.

[123] KENWAY G K W, MARTINS J R R A. Multipoint aerodynamic shape optimization investigations of the common research model wing[J]. AIAA Journal, 2016, 54(1): 112-128.

[124] KENWAY G K W, MARTINS J R R A. Aerodynamic shape optimization of the CRM configuration including buffet-onset conditions: AIAA-2016-1294[R]. Reston: AIAA, 2016.

[125] LIEM R, KENWAY G K W, MARTINS J R R A. Multi-mission aircraft fuel burn minimization via multipoint aerostructural optimization[J]. AIAA Journal, 2015, 53(1): 104-122.

[126] 张科施， 韩忠华， 李为吉， 等. 一种考虑气动弹性的运输机机翼多学科优化方法[J]. 空气动力学学报， 2008， 26(1): 1-7.

ZHANG K S, HAN Z H, LI W J, et al. A method of coupled aerodynamic/structural integration optimization for transport-wing design[J]. Acta Aerodynamica Sinica, 2008, 26(1):1-7 (in Chinese).

[127] KENWAY G K W, KENNEDY G J, MARTINS J R R A. Scalable parallel approach for high-fidelity steady-state aeroelastic analysis and derivative computations[J]. AIAA Journal, 2014, 52(5): 935-951.

韩忠华男， 博士， 教授， 博士生导师。主要研究方向： 代理模型理论与算法， 气动与多学科优化设计， 转捩预测与自然层流翼型/机翼设计, 气动数据库技术。

Tel.: 029-88492704

E-mail: hanzh@nwpu.edu.cn

*Correspondingauthor.Tel.：029-88492704E-mail:hanzh@nwpu.edu.cn

Krigingsurrogatemodelanditsapplicationtodesignoptimization:Areviewofrecentprogress

HANZhonghua*

NationalKeylaboratoryofScienceandTechnologyonAerodynamicDesignandResearch,SchoolofAeronautics,NorthwesternPolytechnicalUniversity,Xi’an710072,China

Overthepasttwodecades,surrogatemodelinghas

muchattentionfromtheresearchersintheareaofaerospacescienceandengineeringduetoitscapabilityofgreatlyimprovingtheefficiencyofdesignoptimizationwhenhigh-fidelitynumericalanalysisisemployed.Designoptimizationviasurrogatemodelsisintensivelyresearchedandeventuallyleadstoanewtypeofoptimizationalgorithmwhichiscalledsurrogate-basedoptimization(SBO).Amongtheavailablesurrogatemodels,suchaspolynomialresponsesurfacemodel,radial-basisfunctions,artificialneutralnetwork,support-vectorregression,multivariateinterpolationorregression,andpolynomialchaosexpansion,Krigingmodelisthemostrepresentativesurrogatemodelwhichhasgreatpotentialinengineeringdesignandoptimization.Inthecontextofaircraftdesign,thispaperreviewsthetheory,algorithmandrecentprogressforresearchesontheKrigingsurrogatemodel.First,thefundamentaltheoryandalgorithmofKrigingmodelarebrieflyreviewedandtheexperienceabouthowtoimprovetherobustnessandefficiencyispresented.Second,threemajorbreakthroughsofKrigingmodelinrecentyearsarereviewed,includinggradient-enhancedKriging,CoKrigingandhierarchicalKriging.Third,theoptimizationmechanismandframeworkofsurrogate-basedoptimizationusingKrigingmodelarediscussed.Inthemeanwhile,theconceptofinfill-samplingcriterionandsuboptimizationispresented.Fiveinfill-samplingcriteriaaswellasthededicatedconstrainthandlingmethodsaredescribed.Furthermore,thenewlydevelopedlocalEI(expectedimprovement)methodandterminationcriteriaforSBOareintroduced.Fourth,anumberoftestcasesincludingbenchmarkoptimizationproblemsaswellasaerodynamicandmultidisciplinarydesignoptimizationproblemsaregiventodemonstratetheexcellentperformanceandgreatpotentialofthesurrogate-basedoptimizationusingKrigingmodel.Atlast,thekeychallengesaswellasfuturedirectionsaboutthetheory,algorithmandapplicationsarediscussed.

optimizationmethod;Kriging;surrogatemodel;aircraftdesign;multidisciplinarydesignoptimization(MDO)

2016-01-05；Revised2016-01-27；Accepted2016-03-15；Publishedonline2016-03-291455

URL：www.cnki.net/kcms/detail/11.1929.V.20160329.1455.004.html

NationalNaturalScienceFoundationofChina(11272265)

2016-01-05；退修日期2016-01-27；录用日期2016-03-15； < class="emphasis_bold">网络出版时间

时间：2016-03-291455

www.cnki.net/kcms/detail/11.1929.V.20160329.1455.004.html

国家自然科学基金 (11272265)

*

.Tel.：029-88492704E-mailhanzh@nwpu.edu.cn

韩忠华．Kriging模型及代理优化算法研究进展J． 航空学报,2016,37(11):3197-3225.HANZH.KrigingsurrogatemodelanditsapplicationtodesignoptimizationareviewofrecentprogressJ.ActaAeronauticaetAstronauticaSinica,2016,37(11):3197-3225.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2016.0083

V211.3

A

1000-6893(2016)11-3197-29