轴流压气机机匣变形对多排转子流场特性的影响

陈颖秀， 侯安平,*， 张明明， 张思牧

1.北京航空航天大学 能源与动力工程学院， 北京 100083

2.北京工业大学 北京科学与工程计算研究院， 北京 100124

轴流压气机机匣变形对多排转子流场特性的影响

陈颖秀1， 侯安平1,*， 张明明2， 张思牧1

1.北京航空航天大学 能源与动力工程学院， 北京 100083

2.北京工业大学 北京科学与工程计算研究院， 北京 100124

在实际轴流压气机加工、装配、使用过程中,机匣的圆度控制、叶片的高度控制、转子和机匣之间的同轴度控制等都普遍存在误差，意味着叶尖间隙的不均匀性必然地存在于每台压气机中。随着对轴流压气机流动研究的不断深入，叶尖周向非均匀间隙成为了需要考虑的问题。针对由机匣变形造成的非均匀叶尖间隙，研究了其对多排转子流场特性的影响。首先介绍了表征机匣变形程度的新参数，进而引进了非轴对称压气机模型的建模方法。针对3种不同的间隙周向布局，采用定常和非定常方法进行了数值模拟，对比了均匀与非均匀间隙下多排转子的气动性能，分析了机匣变形对气动损失分布和传播的影响，并研究了非均匀间隙下非定常压力和气动力的脉动特征。结果表明：非均匀间隙会降低转子性能，转子叶排叶尖区域的流场在非均匀间隙下呈现明显的周向非对称性，在上游叶排“尾迹”的干扰下，后排转子叶尖流场的周向非对称性要大于前排转子。非均匀间隙布局与各叶片气动力分布呈现明显的对应关系，小间隙区域叶片的气动力高，大间隙区域叶片气动力相对较低，从而增加了非均匀间隙下转子叶片的气动力幅值。

机匣变形； 非均匀间隙； 性能； 非对称流场； 气动力

在间隙均匀的理想情况下，已有大量研究证实间隙大小对轴流压气机的流动结构有重要影响[1-4]。然而在压气机加工装配过程中，机匣的圆度控制、叶片高度的控制、转子和机匣之间的同轴度控制等都普遍存在误差，真实压气机很难保证间隙均匀的理想情况。叶尖间隙的不均匀必然存在于每台压气机中，其不均匀程度取决于加工和安装精度的控制。这种间隙的非均匀现象会改变压气机的特性，使其偏离理想的设计状态，而其对性能和流场的影响程度目前尚不清楚，国内外鲜有公开文献进行相关的研究。非均匀间隙通常被分为两类：静止非均匀间隙和旋转非均匀间隙[5]。其中，静止非均匀间隙的周向间隙分布在绝对坐标系下是固定不变的，通常由机匣变形和转子偏心引起；而旋转非均匀间隙则表现为不断变化的周向间隙分布，一般由叶片间的长短差异或转轴弯曲引起。本文主要针对机匣椭圆化变形引起的静止非均匀间隙进行研究。

早期的研究主要关注于非均匀间隙的转子动力学效应，Thomas[6]和Alford[7]发现由偏心引起的非均匀间隙会导致叶片负荷的周向不对称，进而产生切向的旋转诱导力，影响转子动力学稳定性。Song[8-10]、Ehrich[11]和Storace[12]等也通过数值和试验研究对上述现象进行了验证和补充。然而，对非均匀间隙下转子性能、流场方面的研究相对较少。Graf等[5]基于某四级低速压气机，通过试验和简化模型研究了偏心和机匣变形两种周向非均匀间隙对轴流压气机性能和稳定性的影响，结果表明：非均匀间隙会降低压气机的失速裕度和压升系数，而对峰值效率影响较小，其中周向最大间隙是影响失速边界的关键因素。梁武昌等[13]对非均匀间隙进行了相关的试验研究，比较了不同变形机匣下某亚声速孤立转子的性能特性，研究表明，机匣变形会恶化压气机的失速裕度及压升性能。陈颖秀等[14]采用数值方法研究了机匣变形对某跨声速孤立风扇转子性能和流场的影响，定义了参数间隙不均匀度，用以量化机匣的变形程度，并确定了机匣变形下影响风扇性能的两个关键参数：间隙不均匀度和平均间隙，同时对流场进行了详细的分析。

在前期单排风扇转子的研究中发现，机匣变形会在转子下游产生周向不均匀的流场，类似于进气畸变，这可能会对下游叶片造成影响[15-18]。同时，转静叶排的相对转动、转子叶尖间隙的周向变化都会使流场具有明显的非定常性。因此，本文主要针对机匣椭圆化变形引起的叶尖间隙不均匀现象，采用商用软件ANSYS CFX进行定常与非定常数值模拟，研究其对多排转子性能的影响，并分析了多排转子中气动损失的分布与传播特性，同时对比了均匀间隙与非均匀间隙的压力脉动与气动力。

1 数值模型

1.1 机匣变形参数定义

本文首先介绍了新的参数用以表征机匣的变形程度[14]。机匣变形引起的非均匀间隙布局形式如图1所示。图中实线圆形表示转子叶片排，实线椭圆表示变形机匣，虚线圆形表示原始机匣，b为最大间隙，a为最小间隙，c为原始间隙，r为转子叶尖半径，阴影部分面积S为间隙轴向流通面积。

图1 非均匀间隙示意图Fig.1 Sketch of nonuniform clearance

根据上述参数，引进了参数间隙不均匀度=(最大间隙-最小间隙)/最大间隙，用以表征机匣的变形程度，

τ=(b-a)/b

(1)

τ的取值在0～1之间，当周向间隙均匀的时候，最大间隙b等于最小间隙a，τ的值为0；而当机匣变形达到最大程度时，最小间隙a为0，此时间隙不均匀度为1。另一方面，机匣在实际变形过程中周长保持不变，可以得到

Covalized=2π(r+a)+4(b-a)=

Coriginal=2π(r+c)

(2)

式中：Covalized为椭圆机匣周长；Coriginal为原始机匣周长。联立式(1)、式(2)，可以得到最大间隙b和最小间隙a关于间隙不均匀度τ和原始间隙c的式(3)，由于表达式与转子半径r无关，因此能适用不同尺寸的风扇/压气机：

(3)

由式(3)可知，当初始间隙已知时，间隙不均匀度τ能唯一确定最大间隙和最小间隙，从而确定非均匀间隙周向布局。也就是说，对于任意的非均匀间隙布局，总存在一个间隙不均匀度τ与之对应。同时，引进了关键参数平均间隙cave，该参数的定义为cave=S/Covalized≈(a+b)/2。

图2 3种变形机匣非均匀间隙分布Fig.2 Nonuniform clearance layout of 3 deformed casings

本文的研究对象包括前后两排转子和中间的一排静子，前排转子、静子、后排转子的叶片数分别为22、42和34，转子转速为14 617 r/min，进出口叶尖直径分别为315 mm和306 mm，属于跨声速转子。两排转子原始叶尖间隙都设定为0.7 mm，该间隙值是为了便于定性研究非均匀间隙流场特性而人为设定的，并非该多排转子设计的间隙，因此转子性能要低于实际情况。非均匀间隙主要关注中等间隙不均匀度0.5(Multi_Case 0.5)和极限间隙不均匀度0.9(Multi_Case 0.9)2种情况，并将均匀情况间隙不均匀度0(Multi_Case 0)作为参考。图2为3种机匣对应的0°～90° 周向间隙分布，可以发现，在45°周向位置，变形机匣的间隙大小为其平均间隙。机匣变形程度越大，周向间隙差异越大，但平均间隙越小。

1.2 计算模型设置

为了建立椭圆机匣模型，常用的轴对称模型建模方法已然不适用，因此引进了分域建模方法，如图3所示，其中第1排转子命名为R1，随后的静子为S1，下游转子为R2。3排叶片对应的机匣均为椭圆机匣，且前排转子和后排转子非均匀间隙周向布局一致，模拟了真实机匣变形下多排叶片的叶尖间隙布局。同时，假设静子叶片排轮毂处不存在间隙，即静子叶片排对应着轴对称的轮毂和非轴对称的椭圆机匣。分域建模方法将非均匀间隙模型分为内域和外域，其中内域为传统的轴对称模型，而外域包含了椭圆机匣部分，为非轴对称模型，两者在径向的交界面为轴对称的圆柱面，为了便于径向交界面数据传递，设定内域存在微小的均匀间隙，为0.04 mm。每排叶片都被分为内外两部分，即整个计算域共包含6个部分。外域和静子叶排属于静止域，两转子叶片排的内域属于转动域，转静交界面在定常模拟中采用“Frozen rotor”交界面。而在非定常模拟中则采用“Transient rotor-stator”交界面，该设置下，交界面两侧网格的相对位置随时间变化，从而真实模拟转静部件的相对运动。出于加载进出口边界条件的考虑，在轴向进出口处添加了多层网格并与外域连接，数值模拟过程中，进口保持总温、总压及流动方向不变，通过改变出口静压边界条件来调节工作流量。另外，根据椭圆机匣的对称性，内外域模型均选用半周模型进行计算，周向采用旋转周期边界条件，以节约时间和计算资源[19]。本文采用ANSYS CFX进行数值模拟，在单排风扇的研究[14]中校核了分域模型的适用性和计算方法的可靠性，能用于分析流场特征并比较性能相对差异。

综合考虑预测精度和计算时间，计算模型的网格数分别为外域60万、内域240万。在间隙域，总共设置了25层、共83万网格，其中4层在内域。基于k-e湍流模型的使用，转子区域壁面网格衡量参数y+值控制在30左右，一方面满足了壁面函数要求，另一方面保证了壁面网格合理的分辨率[20]。

在定常计算中，以进出口流量差1%为标准来判定结果是否收敛。对于非定常计算，采用了双时间步的方法，即包含物理时间步及各物理时间步下的虚拟时间步，其中物理时间步基本不受稳定性限制，但会影响精度。综合考虑所要捕捉的特征频率以及计算的精度，物理时间步长设置为4.887×10-6s，即转子转到一圈经历840个时间步，确保该非定常计算能捕捉足够高的频率并具有较好的精度[21]。

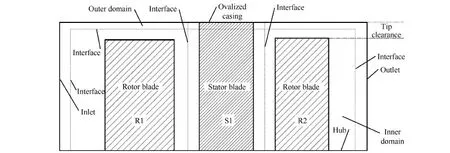
图3 分域模型示意图Fig.3 Sketch of divided domain

2 结果与讨论

首先根据定常结果，比较了该多排转子在不同间隙布局下的特性曲线，研究机匣变形对多排转子性能的影响；随后，综合Multi_Case 0.9的定常和非定常结果，研究了机匣变形下多排转子气动损失的分布特征及其传播特性；最后，从压力脉动和气动力的角度研究了均匀间隙和非均匀间隙下转子非定常流场的差别。

2.1 定常性能分析

表1是对应多排转子3种不同机匣变形程度的非均匀间隙分布，包括最大间隙、最小间隙和平均间隙等参数。由于非均匀间隙的分布与转子半径无关，只与间隙不均匀度和原始间隙相关，因此第1排转子和第2排转子的非均匀间隙分布一致。

表1 3种机匣的主要参数Table 1 Key parameters of three casings

图4是上述3种变形机匣情况下该多排转子的特性曲线。定性上看，实际机匣变形对失速边界有很大的影响，其次是压比，而对效率的影响较小。从压比特性曲线可以看出，间隙和非均匀间隙的差别主要在小流量的工作状态下。

为了定量比较不同非均匀间隙的失速边界，引进了综合失速裕度SM，其表达式为

(4)

图4 3种变形机匣下性能曲线Fig.4 Performance curves with 3 deformed casings

根据上述定义，定量得到间隙不均匀度从0增大到0.9的过程中，失速裕度相对降低44.9%，而峰值压比和效率相对下降了2.52%和0.16%。

2.2 机匣变形下气动损失分布与传播

2.2.1 机匣变形下气动损失分布

根据Multi_Case 0.9近失速状态的定常结果，图5展示了非均匀间隙下不同叶高截面小间隙区域和大间隙区域的熵值云图。随着叶高的增加，各排叶片通道截面的损失逐渐增大，即越靠近间隙，二次流损失越明显。比较大间隙区域和小间隙区域的损失分布云图可以发现，相比于前排转子，第2排转子的相对损失范围更大，由于前后排转子大小不一，相对的损失范围是根据各自的通道而言。比较大间隙和小间隙区域，不论是第1排转子通道还是第2排转子通道，大间隙区域的损失范围要远大于小间隙区域影响范围。通过单级转子的分析结果可知[14]，叶尖二次流的损失主要是由叶尖泄漏引起的，这说明大间隙区域的泄漏涡影响范围更大，并且后排转子的泄漏涡相对影响范围更大，损失的边界线(泄漏涡与主流的交界线)更贴近叶片前缘。

图5 不同叶高截面大小间隙区域熵值云图 Fig.5 Entropy contours of large and small clearance regions at different blade spans

根据Multi_Case 0.9近失速状态的定常结果，还分析了各排叶片叶中截面熵值云图，如图6所示。可以发现，3排叶片的熵值分布都存在明显的周向非对称性。第1排和第2排的高熵流动主要集中于大间隙区域，并且第2排的流动要比第1排转子流动更恶劣。观察静子叶排的熵值云图发现，在与转子大间隙区域对应的周向位置并未出现明显的高熵区。这说明第1排转子叶片产生的周向非对称流场对静子叶片影响不大。也就是说，众多静子的存在使原先周向非对称的流场趋于周向对称。可以推测，第1排转子的周向非对称流动对第2排转子的影响很小。

为了研究上述机匣变形下气动损失的传播规律，本文对周向非对称流场在轴向和周向的流动变化进行了研究。根据某时刻的非定常结果，图7 显示了99%叶高截面3排叶片的周向静熵分布。在非均匀间隙的影响下，无论是静子还是转子的流场都存在明显的周向非对称性，并且转子叶排流场的非对称程度要远大于静子叶排。对比R1、R2转子叶排，虽然两者进气条件不同(R1为均匀进气，R2为非均匀进气)，但是两转子周向非对称流场的分布形式几乎一致，这说明转子的周向非对称流场主要是由自身的非均匀间隙引起的。而对于S1静子叶排，其流场的周向非对称性则是由前排转子引起的，图7清晰展示了该周向非对称流场的传播。根据相关文献可知，叶尖流场的高熵区域主要是由叶尖泄漏涡引起的，叶片经过大间隙区域泄漏涡增大，随着叶片转动，泄漏涡“尾迹”周期性扫过下游静子，导致静子通道出现沿流向“分层”的流场。与传统的叶片尾迹相比，泄漏涡“尾迹”在传播过程中更容易扭曲、变形、扩散。

图6 近失速点各排叶片50%弦长截面熵值云图Fig.6 Entropy contours at 50% axial chord of each blade rows near stall conditions

图7 99%叶高截面熵值云图Fig.7 Entropy contours at 99% blade span

2.2.2 机匣变形下气动损失周向传播

根据非定常结果，图8展示了转子转动半周(1/2 revolution, 1/2 rev)过程中5个时刻的流场分布，图中叶片位置在不同时刻保持不变，其中实线表示大间隙区域的位置，虚线表示小间隙区域的位置。从图中可以看出，大间隙区域始终对应着转子通道的高熵区域。对于转子叶片，其在转动过程中对应的叶尖间隙不断变化，从而导致其周围流场的变化。因此由于变形机匣的存在，转子将会受到两倍转频的激励。而对于静子叶片排，其高熵区域与静子叶片的相对位置保持不变，这说明机匣变形引起的非对称流场不会对静叶产生额外激励。另外，静子叶排的高熵区域偏离了最大间隙位置，其原因如下：静子叶片排的周向非对称流场是由上游转子叶片排产生的，转子经过大间隙区域，带出了具有高熵值的流体，而该流体在沿轴向传播的过程中会跟随叶片往转动方向偏转，最后进入静子叶片排，从而导致该静子叶排的高熵区域偏离了最大间隙位置。

图8 不同周向位置各叶排99%叶高截面熵值云图Fig.8 Entropy contours at 99% blade span of each blade row in different circumferential positions

2.2.3 机匣变形下气动损失轴向传播

对于R1转子，由于其进气条件是均匀的，因此可以知道其叶排流场的周向非对称性是由自身非均匀间隙引起的。而对于后排转子R2，其自身具有非均匀间隙，同时叶排的进气条件是周向非对称的，两种因素都会造成流场的周向非对称性。为了比较自身非均匀间隙和不均匀进气条件(由前排转子非均匀间隙引起)的影响，下文对某时刻的非定常结果从不同角度进行了分析。图9展示了不同叶高截面(85%、90%、95%和97%)各叶排流场的周向静熵分布。在97%叶高处，3排叶片的流场都呈现明显的周向非对称性，并且后排转子的非对称程度要大于前排转子。随着叶高截面的降低，流场非对称程度逐渐减弱。在90%截面处，前排转子R1和静子S1叶排的流场是周向对称的，即R2转子的进气条件趋于周向对称，然而R2叶排的流场依旧呈现较为明显的周向非对称性。这说明后排转子R2的非对称流场主要是由其自身的非均匀间隙产生的，同时后排转子进口的非均匀进气必然会加剧该流场的非对称程度，从而导致后排转子的周向非对称性大于前排转子。

图9 不同叶高截面熵值云图 Fig.9 Entropy contours at different blade spans cross-section

为了进一步比较前后排转子的差异，图10展示了两排转子大间隙区域叶片通道内不同截面的泄漏涡流线以及其速度。对于前排转子，泄漏涡沿通道发展，其影响范围先逐渐增大，随后减小，当到达相邻叶片尾缘时，泄漏涡逐渐消失，并与主流混合，如图10中①所示。对于后排转子，其泄漏涡在径向的影响范围要明显大于前排转子，这说明图9中前后排转子的差异是由各自不同的泄漏涡引起的。图中②、③的流场细节揭示了R2通道内泄漏涡始终具有较大影响范围的原因。对于②，泄漏涡在靠近叶背的局部区域，而该截面的低速区域位于通道中间，两者之间存在偏差。若来流均匀，则低速区应与涡的位置一致，两者的偏差意味着通道来流是不均匀的，通过上文分析得知该不均匀流可能由静子尾迹和前排转子泄漏涡“尾迹”造成。在R2通道内，上游“尾迹”与泄漏涡相互干涉，减缓了泄漏涡的耗散，使其保持较大的影响范围。另一方面，如③所示，上一通道内未完全掺混于主流的泄漏涡会与相邻通道的泄漏涡在叶片尾缘掺混，从而扩大泄漏涡的影响范围。在这几方面的共同作用下，后排转子的叶尖二次流损失要大于前排转子。

图10 前后排转子通道横截面流线图 Fig.10 Streamline at cross-sections of rotor blade passages

2.3 机匣变形下非定常压力脉动分析

为了研究多排转子在非均匀间隙下的流场特性，本节分析了其非定常压力脉动特征，并与其均匀间隙下的流场进行了对比。

在多排转子中，3排叶片周围设置了多个监测点，各排叶片在85%、99%叶高以及叶尖间隙共设置了多个监测点。

为了比较均匀间隙(Multi_Case 0)和非均匀间隙(Multi_Case 0.9)轴向不同位置压力脉动的差别，分布在各排叶片前后选取两个监测点，监测点示意图如图11所示，其中M1、M2相对R1静止，M3、M4相对S1静止，M5、M6相对R2静止。图12是均匀间隙下该6个监测点的压力脉动频谱图。

图11 轴向监测点示意图Fig.11 Sketch of monitors in axial direction

根据转速14 617 r/min可以得知，转子的转动频率是243.6 Hz，结合3排叶片的数目22、42和34，便可得各排叶片的通过频率，如表2所示。因此图12中5 356 Hz、8 278 Hz和10 225 Hz分别对应R1、R2和S1的通过频率。

在均匀间隙下，R1转子前的压力脉动很小，而在该转子后方，由于受到后排静子的影响，压力脉动出现10 225 Hz的占优频率，这是静子叶片排的通过频率。对于S1静子，叶片排前的监测点感受到5 356 Hz的频率，该频率是前排转子的通过频率。在S1静子后方M4测点位置，压力脉动多出了8 278 Hz及其二倍频的占优频率，即感受到了R2转子的通过频率。在R2转子的前尾缘，压力脉动仅存在一个占优频率，即S1静子的通过频率10 225 Hz。各叶片排的压力脉动频率均为相邻叶片排的通过频率。

图12 Multi_Case 0监测点频谱图Fig.12 Frequency spectrum of monitors (Multi_Case 0)

表2 各排叶片的通过频率Table 2 Passing frequency of each blade row

Hz

图13是非均匀间隙下上述6个监测点的压力脉动频谱图。与均匀间隙相比，R1转子前尾缘都增加了487 Hz的压力脉动频率。487 Hz是转子转动频率的二倍频，其产生的原因如下：机匣变形情况下存在2个大间隙区域和2个小间隙区域，大间隙区域叶片间隙压力要低于小间隙区域压力，因此转子转动一周过程中叶片间隙的压力周期性脉动二次。另外，转子前487 Hz的压力脉动幅值要高于转子后的脉动幅值，即机匣变形引起的压力脉动在通过转子后会被减弱。类似的现象在R2转子中同样能观察到。而对于静子前后的压力脉动，机匣变形对其脉动幅值和脉动频率的影响均不明显。

2.4 机匣变形下叶片非定常气动力分析

根据2.3节分析，非均匀间隙下压力脉动会更加强烈，这将直观体现在叶片的非定常气动力上。对于各叶片来说，流场内部的压力脉动直接影响到叶片表面的压力脉动，气动力作为叶片表面的压力积分，其随时间的脉动特征是影响叶片的气动弹性稳定性的重要因素。

图13 Multi_Case 0.9监测点频谱图Fig.13 Frequency spectrum of monitors (Multi_Case 0.9)

图14对比了均匀与非均匀间隙下R1、S1和R2叶排某叶片的非定常气动负荷，无论是均匀还是非均匀间隙，各排叶片气动力都有较明显的非定常变化，这是由级间环境引起的。在非均匀间隙的影响下，转子叶片气动力幅值要大于均匀间隙的情况，而非均匀间隙对静子叶片的气动力影响很小。当转子叶片转动到大间隙位置时，其表面气动力较小，而叶片转动小间隙位置时，气动力会相应地增大。比较R1和R2的气动力时域曲线还可以发现，R1转子时域曲线中高气动力与低气动力范围较为对称，而R2转子时域曲线中低气动力的范围更大，这意味着R2叶排“大间隙区域”的扇区更大。实际上“大间隙区域”往往对应着高熵流动，在R1转子泄漏涡“尾迹”的影响，R2叶排的高熵流动区域被拓宽，从而导致R2转子时域曲线中波峰和波谷的不对称。

对于R1叶片排，其均匀间隙下非定常气动力幅值较小，从而使得非均匀间隙对气动力的影响相对突出，定量而言，非均匀间隙下非定常气动力的幅值约为均匀间隙情况的5倍。对于S1静子叶排，非均匀间隙对叶片的非定常气动力影响很小，非均匀间隙与均匀间隙的非定常气动力幅值几乎一致，这是因为变形机匣相对于静子叶排是静止的，不会对其产生额外的气动激励。对于R2转子，由于R2叶片受到前排静子的尾迹干扰，级间影响相对较大，均匀间隙下非定常气动力幅值较大，使得非均匀间隙对气动力的影响相对较小，非均匀间隙下非定常气动力的幅值约为均匀间隙情况的2.2倍。

图15和图16分别是均匀间隙和非均匀间隙下R1、S1和R2叶片的气动力频谱图。在均匀间隙下，各排叶片表面气动力的脉动规律与图13中压力的脉动规律类似。转子气动力的占优频率是静子的通过频率，而静子的气动力频率包含了前后排转子的占优频率。

图14 均匀与非均匀间隙叶片气动力对比Fig.14 Comparison of aerodynamic force between uniform and nonuniform clearance

图15 均匀间隙气动力频谱Fig.15 Frequency spectrum of aerodynamic force with uniform clearance

图16 非均匀间隙气动力频谱Fig.16 Frequency spectrum of aerodynamic force with nonuniform clearance

对于非均匀间隙的情况，R1和R2转子的气动力出现了487 Hz的占优频率，并且其对应的脉动幅值最大，这是由机匣变形产生的。除487 Hz的频率以外，3排叶片其他特征频率及相应的幅值变化不大。这说明非均匀间隙会使转子气动力产生额外的脉动特征，而对原有的脉动频率及幅值影响不大。分析静子的气动力频率可以发现，上游487 Hz的频率并未出现，仅感受到上下游转子叶片的通过频率。这是因为机匣与静子叶片相对静止，机匣的变形产生的周向非对称流场与静子没有相对的“转动”，因此静子不会感受到487 Hz的频率。

3 结 论

1) 机匣变形会降低轴流压气机性能，其对失速裕度的影响最大，压比次之，对效率的影响最小。

2) 对于非均匀间隙下的多排转子，在上游静子尾迹和前排转子泄露涡“尾迹”共同影响下，后排转子的叶尖二次流损失要大于前排转子，其流场损失更大，周向不对称程度更高。

3) 机匣变形会改变转子域流场的压力脉动频率和幅值，对转子叶片产生额外的激励，但对静子叶排几乎没有影响。

4) 非均匀间隙布局与各叶片气动力分布呈现明显的对应关系，小间隙区域叶片的气动力高，大间隙区域叶片气动力相对较低，从而增加了非均匀间隙下转子叶片气动力幅值。

[1] SMITH L H. The effect of tip clearance on the peak pressure rise of axial-flow fans and compressors[Z]. ASME Symposium on Stall, 1958: 149-152.

[2] BAGHDADI S. Modeling tip clearance effects in multistage axial compressors[J]. Journal of Turbomachinery, 1996, 118(4): 697-705.

[3] SMITH L H. Casing boundary layers in multistage axial flow compressors[J]. Flow Research on Blading, 1970， 106(1)： 635-647.

[4] CHRISTOPHER H, RICHARD W, GARY P. Effect of tip clearance on fan noise and aerodynamic performance: AIAA-2005-2875[R]. Reston: AIAA, 2005.

[5] GRAF M B, WONG T S, GREITZER E M, et al. Effects of nonaxisymmetric tip clearance on axial compressor performance and stability[J]. Journal of Turbomachinery， 1998, 120(4): 648-661.

[6] THOMAS H J. Unstable natural vibration of turbine rotors induced by the clearance flow in glands and blading[J]. Bulletin de L’A.I.M., 1958,71(11/12): 1039-1063.

[7] ALFORD J. Protecting turbomachinery from self-excited rotor whirl[J]. Journal of Engineering for Power, 1965, (87): 333-343.

[8] SONG S J, MARTINE-SANCHEZ M. Rotordynamic forces due to turbine tip leakage: part 1—Blade scale effects[J]. Journal of Turbomachinery, 1997, 119(4): 695-703.

[9] SONG S J, MARTINE-SANCHEZ M. Rotordynamic forces due to turbine tip leakage: part 2—Radius scale effects and experimental verification[J]. Journal of Turbomachinery,1997, 119(4): 704-713.

[10] SONG S J. Inviscid rotor dynamic damping forces due to nonaxisymmetric tip clearance in turbines[J]. AIAA Journal, 1998, 36(12): 2163-2169.

[11] EHRICH F. Rotor whirl forces induced by the tip clearance effect in axial flow compressors[J]. ASME Journal of Vibration and Acoustics, 1993, 115(4): 509-515.

[12] STORACE A, EHRICH F, SONG S J, et al. Unsteady flow and whirl-inducing forces in axial-flow compressors: part I—Experiment[J]. Journal of Turbomachinery, 2001, 123(3): 433-445.

[13] 梁武昌， 楚武利， 朱俊强, 等. 非轴对称尖部间隙对轴流压气机性能影响的实验研究[J]. 航空动力学报， 2004, 19(2): 233-236.

LIANG W C, CHU W L, ZHU J Q, et al. Effect of asymmetric tip clearance on axial flow compressor performance[J]. Journal of Aerospace Power, 2004, 19(2): 233-236 (in Chinese).

[14] CHEN Y X, HOU A P, ZHANG M M, et al. Effects of nonuniform tip clearance on fan performance and flow field: ASME-GT2015-42133[R]. New York: ASME, 2015.

[15] RABE D. Influence of inlet distortion on transonic compressor blade loading: AIAA-1995-2461[R]. Reston: AIAA, 1995.

[16] DONG X, SUN D, LI F, et al. Effects of rotating inlet distortion on compressor stability with SPS casing treatment[J]. Journal of Fluids Engineering, 2015, 112(29): 59-60.

[17] DANIELE C L, TEREN F. Prediction of compressor stall for distorted and undistorted inlet flow[J]. Journal of Aircraft, 1975, 12(10): 841-846.

[18] SPAKOVSZKY Z S, WEIGL H J, PADUANO J D, et al. Rotating stall control in a high-speed stage with inlet distortion: part II—Circumferential distortion[J]. Journal of Turbomachinery, 1999, 121(3): 517-524.

[19] ANSYS. Computational fluid dynamics soft ware package user guide[CP/DK]. Canonsburg, PA： ANSYS, Inc., 2014.

[20] MENTER F R. Two-equation eddy-viscosity turbulence models for engineering applications[J]. AIAA Journal, 1994, 32(8): 1598-1605.

[21] MONTOMOLI F, NAYLOR E, HODSON H P, et al. Unsteady effects in axial compressors: A multistage simulation[J]. Journal of Propulsion & Power, 2013, 29(5): 1001-1008.

陈颖秀男， 博士研究生。主要研究方向： 压气机非均匀流动特性， 叶轮机械气动弹性稳定性。

Tel.: 010-82313700

E-mail: cyxiu1991@163.com

侯安平男， 博士， 副教授。主要研究方向： 叶轮机械气动弹性， 压气机气动设计, 气浮高速电机。

Tel.: 010-82316624

E-mail: houap@buaa.edu.cn

张明明男， 博士， 讲师。主要研究方向： 叶轮机械气动弹性， 压气机气动稳定性。

Tel.: 010-82313700

E-mail: mmzhang@bjut.edu.cn

*Correspondingauthor.Tel.：010-82316624E-mail:houap@buaa.edu.cn

Effectsofcasingdeformationonbladerowsflowfieldcharacteristicsinanaxial-flowcompressor

CHENYingxiu1,HOUAnping1,*,ZHANGMingming2,ZHANGSimu1

1.SchoolofEnergyandPowerEngineering,BeihangUniversity,Beijing100083,China2.BeijingCenterforScientificandEngineeringComputing,BeijingUniversityofTechnology,Beijing100124,China

Intheactualmachining,installationandusingprocess,theproblemsofcasingdeformation,rotoreccentricityandnonuniformrotorbladeheightsexisttosomeextentinallaxial-flowcompressors,resultingincircumferentialnonuniformtipclearance.Withthedeepeningoftheresearchonaxial-flowcompressorflow,thenonuniformclearancebecomestheproblemshouldbeconsidered.Thefocusofthisinvestigationisonthenonuniformclearancecausedbycasingdeformationanditseffectontheflowfieldcharacteristicsoftherotorrows.Thenewparameterrepresentingthenonuniformityoftipclearanceisrecommended,andthemodelingapproachforthenonaxisymmetrycompressorisintroduced.Threenumericalmodelswithdifferenttipclearancenonuniformitiesareinvestigatedbybothsteadyandunsteadycalculations.Theeffectsofnonuniformclearanceonaerodynamicperformanceandflowlossdistributionareanalyzed.Theunsteadypressurefluctuationandaerodynamicforcearealsodiscussed.Theresultsindicatethatthenonuniformclearancecancontributetoperformancedegradationandthecircumferentialasymmetricalflowfieldinbladetipregions.Duetothe“wake”oftheupstreambladerow,flowfieldasymmetryofthebackrotorrowismoreobviousthanthatofthefrontrotorrow.Thereisdirectcorrespondencebetweenthenonuniformclearancelayoutandtheaerodynamicforcedistributioninthecircumferentialdirection.Thebladeaerodynamicforceishigheratsmalltipclearanceregionsandloweratlargetipclearanceregions,increasingtheamplitudeoftheaerodynamicforceincasingdeformation.

casingdeformation;nonuniformtipclearance;performance;asymmetricalflow;aerodynamicforce

2015-11-11；Revised2015-12-04；Accepted2016-01-06；Publishedonline2016-01-181513

URL：www.cnki.net/kcms/detail/11.1929.V.20160118.1513.008.html

NationalNaturalScienceFoundationofChina(51306003)

2015-11-11；退修日期2015-12-04；录用日期2016-01-06； < class="emphasis_bold">网络出版时间

时间：2016-01-181513

www.cnki.net/kcms/detail/11.1929.V.20160118.1513.008.html

国家自然科学基金 (51306003)

*

.Tel.：010-82316624E-mailhouap@buaa.edu.cn

陈颖秀， 侯安平， 张明明， 等． 轴流压气机机匣变形对多排转子流场特性的影响J． 航空学报,2016,37(11):3284-3295.CHENYX,HOUAP,ZHANGMM,etal.Effectsofcasingdeformationonbladerowsflowfieldcharacteristicsinanaxial-flowcompressorJ.ActaAeronauticaetAstronauticaSinica,2016,37(11):3284-3295.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2016.0010

V231.3

A

1000-6893(2016)11-3284-12