借助信息技术平台，化解 直角坐标系中等腰直角三角形问题

江苏省淮安市淮阴区开明中学　史燕萍

借助信息技术平台，化解直角坐标系中等腰直角三角形问题

江苏省淮安市淮阴区开明中学史燕萍

以平面直角坐标系为载体，加上等腰直角三角形的条件，易形成综合性较强的问题，此类题型往往将点坐标知识、等腰三角形性质、三角形全等、勾股定理等知识贯穿其中，并运用数形结合、分类讨论的数学思想解决问题。而运用信息技术，进行资源整合，优化此类问题的解法，可提高学生的综合能力。

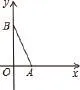
一、运用课件展示图形，根据等腰三角形“三线合一”求点坐标

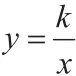
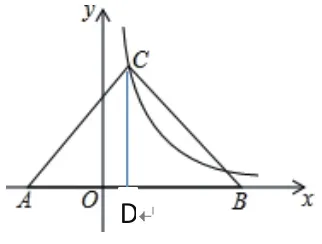
（1）求k的值和边AC的长；

（2）求点B的坐标。

二、运用信息技术将三角形旋转变化，根据三角形全等得等量关系

例2将等腰直角△ABC斜放在平面直角坐标系中，使直角顶点C与点（1，0）重合，点A的坐标为（-2，1）。

（1）求△ABC的面积S；（2）求直线AB与y轴的交点坐标。

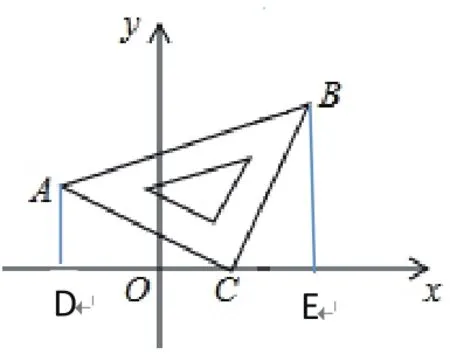
【分析】（1）证△ACD≌△CBE，

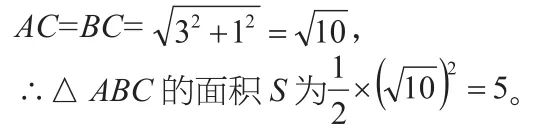
【点评】作辅助线构造三角形全等得到对应边相等是解决问题的关键。

三、运用信息技术作出辅助线，根据分类讨

论思想画出两种图形

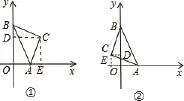
例3如图，在平面直角坐标系中，点A（2，0）、B（0，4），以AB为斜边作等腰直角△ABC，则点C坐标为_____________。

【分析】由于题中点C的位置不确定，所以有图①图②两种情况，需要分类讨论，并作辅助线根据全等得结论。

【点评】本题考查了坐标与图形性质、全等三角形的判定与性质、等腰直角三角形的性质；难点在于分类思想的运用。

四、运用信息技术展示旋转过程，根据数形结合思想得到数量关系

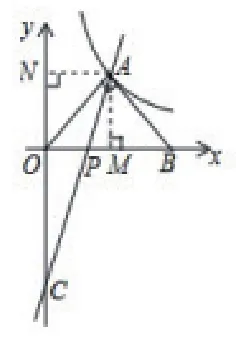
图1

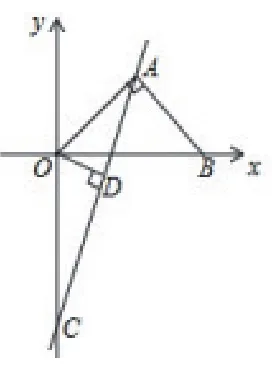
图2

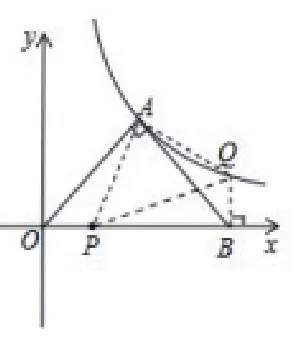
图3

（1）求k的值；

（2）如图2，过点O作OD⊥AC于D，求CD2-AD2的值；

（3）如图3，将△AOB绕点A逆时针旋转，射线AO交x轴正半轴于点P，射线AB交（1）中双曲线上于点Q，△PAQ能否成为以A为直角顶点的等腰直角三角形？若能，求点P，Q的坐标；若不能，说明理由。

【分析】（1）首先过点A作AM⊥x轴于点M，AN⊥y轴于N，则AM=AN，进而得出A点横纵坐标相等，进而代入一次函数解析式求出即可；

（2）由（1）得AD2=OA2-OD2①，CD2=OC2-OD2②，利用②-①：CD2-AD2=OC2-OA2求出即可；

（3）如图易证△AOP≌△ABQ（ASA），再根据OP=BQ可求出点P，Q的坐标。

【点评】此题主要考查了反比例函数综合应用、全等三角形的判定与性质、勾股定理的应用等知识，需利用数形结合找出全等三角形从而得出数量关系。

五、中考真题再现

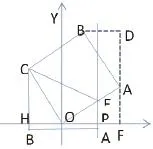
1.（2016镇江）如图，在平面直角坐标系中，坐标原点O是正方形OABC的一个顶点，已知点B坐标为（1，7），过点P（a，0）（a＞0）作PE⊥x轴，与边OA交于点E（异于点O、A），将四边形ABCE沿CE翻折，点A、B分别是点A、B的对应点，若点A恰好落在直线PE上，则a的值等于（）。

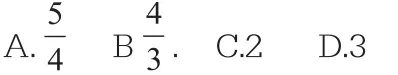
【分析】本题考查了正方形的折叠和全等三角形的判定与性质，解题的关键是通过作辅助线构造三对三角形全等，用字母表示点A的坐标并列出方程求出点A坐标，再进一步得出OP长。理解AE在PE上时，AB与x轴平行并正确作图是难点。

思考与感悟：

1.巧借信息技术进行资源整合

信息技术的丰富资源，为教师提供了海量的教学资源，开阔了视野，激活了思维，为教师打造高效的专题性教学提供了宝贵的素材，也改变学生学习的方式，为学生提供探索复杂问题、多角度理解数学思想的机会，开阔了学生数学探索的视野。

2.变式训练提升学生学习能力

通过信息技术手段进行图形的变化，让学生体会相互间的联系与区别，掌握举一反三解决相关问题的方法与技巧。让学生逐步学会变式，概括总结一类问题的解决策略，学生获得的不仅仅是学习成绩的提升，还有自主高效的学习能力提升。

【备注：本文系省级课题。信息技术条件下初中数学学习资源开发研究的研究成果，课题编号：30102】