数形结合方法在高中数学教学中的运用分析

江苏省句容市实验高级中学　裴贤喜

数形结合方法在高中数学教学中的运用分析

江苏省句容市实验高级中学裴贤喜

数学是研究数量关系与几何空间的学科，能够完整地刻画出社会科学的规律。在高中教学阶段，数学的教学一直都是重点和难点，随着教育事业的不断发展，高中数学教学实践中产生了多种多样的数学教学方法，数形结合就是其中重要的组成部分。通过“数”和“形”的结合，提升学生的思维能力，将复杂的问题简单化，将抽象的问题具体化，能够形成源源不断的解题思路，提高数学成绩。

一、数形结合方法概述

数形结合，顾名思义，就是将数学研究领域中体现数量的“数”和代表空间形式的“形”结合起来，达成一致的效果。数和形通常都是互相依存的关系，抽象的数量问题在一定程度上也具有直观的几何意义，对于图形的性质，也能够通过数量关系加以描述和概括，因此，数和形在一定条件下能够实现互相转化。

数形结合方法是根据大量的教学实践总结而来的，如今被广泛地应用到高中数学教学中，是数学中非常关键的思想和解决难题常用的方法。数形结合方法是总结数学问题条件和结论之间的关系，查看其内在的联系，分析该题代数含义的同时，揭示其具有的直观几何意义，为问题的解决提供一个全新的思路，能够将复杂问题简单化，将抽象问题具体化，扩展学生的解题思路，培养发散性的思维，从而有助于数学成绩的提升。

二、数形结合方法应用的原则

首先是量的积累原则。数学的学习是一个量变到质变的过程，教师应该根据教学内容的特点，精心策划教学环节，在潜移默化中引导学生掌握数形结合的思想，并应用到实践中去。通过大量反复的练习，使学生掌握概念与概念之间的内在联系，善于发现数学结构和数学运算之间的共同点，领悟到数学学习的方法，提升学生的思维创造能力，日积月累，实现教学目标。

其次是启发性的原则。教师要有目的、有针对性地运用启发性原则，引导学生解决数学难题要从实际出发，培养发散性的思维能力，从而掌握解决问题的关键方法。启发性原则的关键就是鼓励学生积极地思考，不断地提出问题，在解决问题的过程中提高自己，锻炼独立思考的能力。

三、运用数形结合方法提高解题能力的教学策略

1.教师转变教学观念

根据新课改的课程要求以及数形结合方法的解题特点，教师必须要转变传统的教学观念，要求学生改变以往的学习方式，使数形结合的方法不仅作为学生解决问题的工具，还应该充分地揭示出其教育意义，深入挖掘其中存在的教育价值，重视对问题分析思路的教学。只有这样，才能够保持数形结合思想的生命力，为学生的发展带来积极的影响，从而为教育研究工作提供强大的理论和实验基础，因此，教师必须要创新发展教学观念，提高教学质量。

2.注重典型案例的教学

在日常的教学中，教师应该重视对典型案例进行重点的讲解，使学生能够举一反三，掌握基本的解题技巧。尤其是在解法比较烦琐的问题上，利用数形结合的方法，在进行精讲前，请学生对问题进行探究，并找到合适的解决方法；在讲解的过程中，引导学生对问题进行积极的思考；讲解完毕之后，请学生对比各种解法的优缺点，总结和归纳各类题型的综合性解法，为日后遇到类似的题型打好基础。这样一来，教师能够在讲解的过程中不断提升自己，完善教学方法，学生能够找到最佳的、适合自己的解题方案，锻炼发散性的思维模式，方便日后的学习。

四、数形结合方法在高中数学教学中的运用

集合是高中数学中重要的知识点，利用数形结合的方法，能够帮助学生看清集合之间的各种关系，利用韦恩图能够处理具体的集合问题，利用数轴能够解决相对模糊的集合问题。例如，在处理A、B集合的包含问题时，可以将两个集合分别放在数轴上，用字母或数字表明相应的点，通过数轴上的大小来判断集合的包含关系，列出不等式进行具体的计算。

利用韦恩图来解决实际的集合问题，通过用圆来表示集合，相交的部分就证明集合之间有相交的元素，反之则表示空集。

例：某高中学生有40名同学报名参加音乐、舞蹈、绘画兴趣小组，报名的情况如下：

第一，40名学生每人至少报名参加一个课外兴趣活动小组。

第二，在没有报名参加音乐兴趣小组的学生中，报名参加舞蹈小组的人数是报名参加绘画人数的二倍。

第三，仅报名参加音乐小组的人数比剩余学生中报名参加音乐小组的多一人。

第四，仅报名参加一个兴趣小组的学生中有一半没有报名参加音乐小组。

问：（1）仅报名参加一个兴趣小组的人数是几人？

（2）有几人参加音乐小组？

分析：本题的数量关系较为复杂，运用一般的方法，难以理解其中的解题思路，教师可以引导学生将报名参加音乐、舞蹈、绘画小组的人分别设为一个集合，用韦恩图方法来表示，问题就能迎刃而解了。

解：设集合A=｛报名参加音乐兴趣小组的人数｝，集合B=｛报名参加舞蹈兴趣小组的人数｝，集合C=｛报名参加绘画兴趣小组的人数｝，如下图所示。

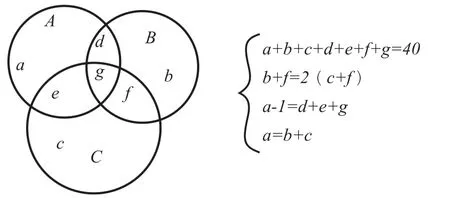
解得：a=11，b=10，c=1，d+e+g=10，a=d+e+f=21。因此得出仅报名参加一个兴趣小组的人数为10名学生，报名参加音乐兴趣小组的人数为21人。

综上所述可知，数形结合方法是高中数学教学中最常见和最有效的思想方法之一，能够将复杂的问题具体化，化繁为简，将抽象的问题具体化，方便学生的理解和记忆，有利于培养学生的发散性思维能力，能够帮助教师完善教学方法，提升教学质量，对整个数学研究工作都有重大的指导性作用。