注重情景分析 培养解题悟性

江苏省清河中学　王志国

注重情景分析培养解题悟性

江苏省清河中学王志国

悟性主要指对事物的理解能力和分析能力，悟性依赖于后天开发和培养。数学习题浩如烟海，解题方法繁多，如果有目的地让学生解一些典型的例题或习题，通过情景分析、探索、变形、拓展，有利于培养学生的解题悟性，掌握解题技巧，提高解题能力。

情景分析；培养；悟性

悟性主要指对事物的理解能力和分析能力，悟性依赖于后天开发和培养。数学习题浩如烟海，解题方法繁多，如果有目的地让学生解一些典型的例题或习题，通过情景分析、探索、变形、拓展，有利于培养学生的解题悟性，掌握解题技巧，提高解题能力。

一、注重情景分析，打破思维定式，培养多向思维

思维定势是能力的桎梏，学生解题，先入为主，方法单一，容易受某个条件、某种形式的影响，产生思维定式。

例如，对于任意的a∈［-1，1］，函数f（x）=x2+（a-4）x-2a的值恒大于0，求x的取值范围。

许多学生在解此题时，凭经验把它归结为二次函数的问题，解法如下：∵x2+（a-4）x-2a=0的两根为2，2-a；

解到此处，学生陷入困境，要得到正确结果还需花上一番功夫。如果启发学生，改变思路：

以自变量，数形结合，很快发现如下解题过程：

设f（x）=x2+4x+a（x-2）

真是“山重水复疑无路，柳暗花明又一村”，至此，学生也明白打破思维定式，培养思维定式的重要性。

二、通过情景分析，适当设置陷阱，疑中起悟，培养思维严密性

科学家李四光有句名言：不怀疑，不能见真理。问题在怀疑中提出，又必然在深入研究中解决，如果针对学生解题的不规范、思维的不严密，适当设置一些陷阱，就可以让学生在失败中找原因，在失败中求成功。

例如，母线长为l的圆锥，轴截面顶角为α，过圆锥顶点的所有截面中，求最大截面的面积。

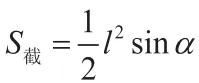
三、通过情景分析，培养横向联系的能力

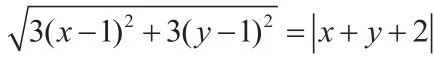
A.椭圆B.圆C.双曲线D.抛物线

情景分析：左边是根式，右边有绝对值，按常规思路两边平方得到：x2+y2-xy-5x-5y+1=0。

很难判断曲线形状，这时，不妨引发学生观察左右两边式子的结构，两边同除以，得到方程，再充分让学生发挥联想，这时有的学生发现，等式左边象两点间距离公式，右边象点到直线的距离。于是通过引导，学生由一个代数方程联想到解析几何知识，由方程联想到圆锥曲线的定义。

通过联想既提高了学生的学习兴趣，又培养了学生对交汇点知识的综合运用能力，这正是高考对学生的要求。

四、通过情景分析，培养类比迁移的能力

A.在（0，+∞）上是增函数；B.在（0，+∞）上是减函数；

C.在（0，1）上是增函数，在（1，+∞）上是减函数；D.是常函数。

这是一道高考模拟题，在解析几何中，学生只学过双曲线标准方程，对本题中双曲线的离心率的求法在形式上相当陌生，难以表示，于是不少学生提出本题超纲，没有学过，不知如何解决。在这种情况下，不妨引导学生用类比的方法先研究标准形式，这样就可以变陌生为熟悉，变难啃为易咽。

通过对同类题目的深入研究，由此及彼，类比迁移，使学生悟出非标准情况下的情形，获得同类问题的通解，使学生疑惑不解到恍然大悟，这样就培养了学生类比迁移的能力。

五、利用网络情景，为学生的“悟”提供平台

把现代信息技术作为学生学习数学和解决问题的强有力工具，致力于改变学生的学习方式，使学生乐意并有更多的精力投入到现实的、探索性的数学活动中去。通过多媒体进行数学教学，它擅长模拟各种动态的或平常无法观察到的现象，使学生有了更多的观察、探索、实验与模拟的机会，从而形成直觉和顿悟，可以做出猜测，又可以通过检验假设，证明自己的猜想，既获得技能，也取得了经验。

实践证明，在教学过程中，通过情景分析，培养学生思维的多向性、发散性和灵活性，以数学知识为载体，激发学生思维活动走向更广阔的空间，对培养他们的解题悟性，有着重要的意义。