如何通过函数的单调性解决参数取值范围的问题

江苏省溧阳市埭头中学 王丽萍

如何通过函数的单调性解决参数取值范围的问题

江苏省溧阳市埭头中学 王丽萍

利用函数的单调性，求参数的取值范围问题，是学生比较棘手的问题，但也并不是无法可循，下面就几个简单的例题来阐述一下个人的观点。

方法一：利用一元二次函数根的大小情况判断函数的单调性，其实就是利用函数的单调增区间D与函数在某一区间I上单调增之间的关系解决问题。

方法二：分离变量法。这种方法要注意在分离变量的过程中不等号的方向是否要改变，最后转化成求函数的最值问题。

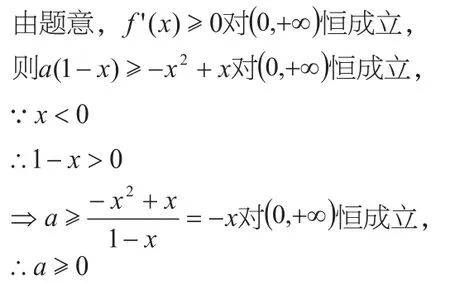
但是有的时候函数的导函数虽然是一个一元二次函数，却不能因式分解。例如：

像这里的一元二次函数，就不能像上述例题一样，简单地通过因式分解求得函数的单调区间去解决问题，即使要求单调区间，也要通过求根公式，过于复杂。但是可以利用研究一元二次函数的对称轴与区间的位置关系，判断端点值的取值情况来解决问题。

故a≥1。

通过上述两个例题，我们可以发现对于研究已知某一三次函数在某区间上的单调性，求参数的取值范围问题，常见方法是两种。方法一：利用它的导数是一元二次函数这一特征，结合一元二次函数的有关性质，即区间根问题，解决问题。但这里面的处理方法有很多种，而这又恰恰是学生学习过程中的一个盲点，学生经常会考虑得不全面，从而影响最后的计算结果。方法二：分离变量法，这种方法还是具有一般性的。一般情况下，可以说这种方法适用于任何一个函数。通过变量分离，最后把问题转换成求一个新的函数的最值问题。当然对于稍复杂点的函数，要求最值，还是要结合函数的单调性来判断。但是这种方法虽然通用，也存在一个问题，就是在分离变量的时候，不等号方向是否有影响，这往往也是学生做题过程中容易忽略并且容易出错的地方。

对于这类问题，学生还有一个容易疏忽的地方，或者说不能深刻理解的地方。下面我们通过一个变式来体现这一问题。

为什么会出现这样的情况？对于最后求得的取值范围，其实对于端点值我们还是要去检验一下的，因为端点值正好是使得。这一检验过程，在前两题的解答过程中就没有体现出来，并不是说明不需要检验。而这一检验过程的重要理论依据是：一般地，可导函数f（x）在某一区间（a，b）内单调递增（减）的充要条件是：（1）；（2）在（a，b）的任何子区间上不恒为0。学生往往会忽略第二个条件。

最后，我们可以发现，由函数在某区间上的单调性，求参数的取值范围问题，可以利用转化与化归的思想，将其转化为“不等式恒成立问题”，最终即为“研究函数的最值问题”，也可以利用函数与方程的思想以及数形结合的思想，转化为“函数图像的交点问题”。